分布式系统-CAP理论
CAP定理
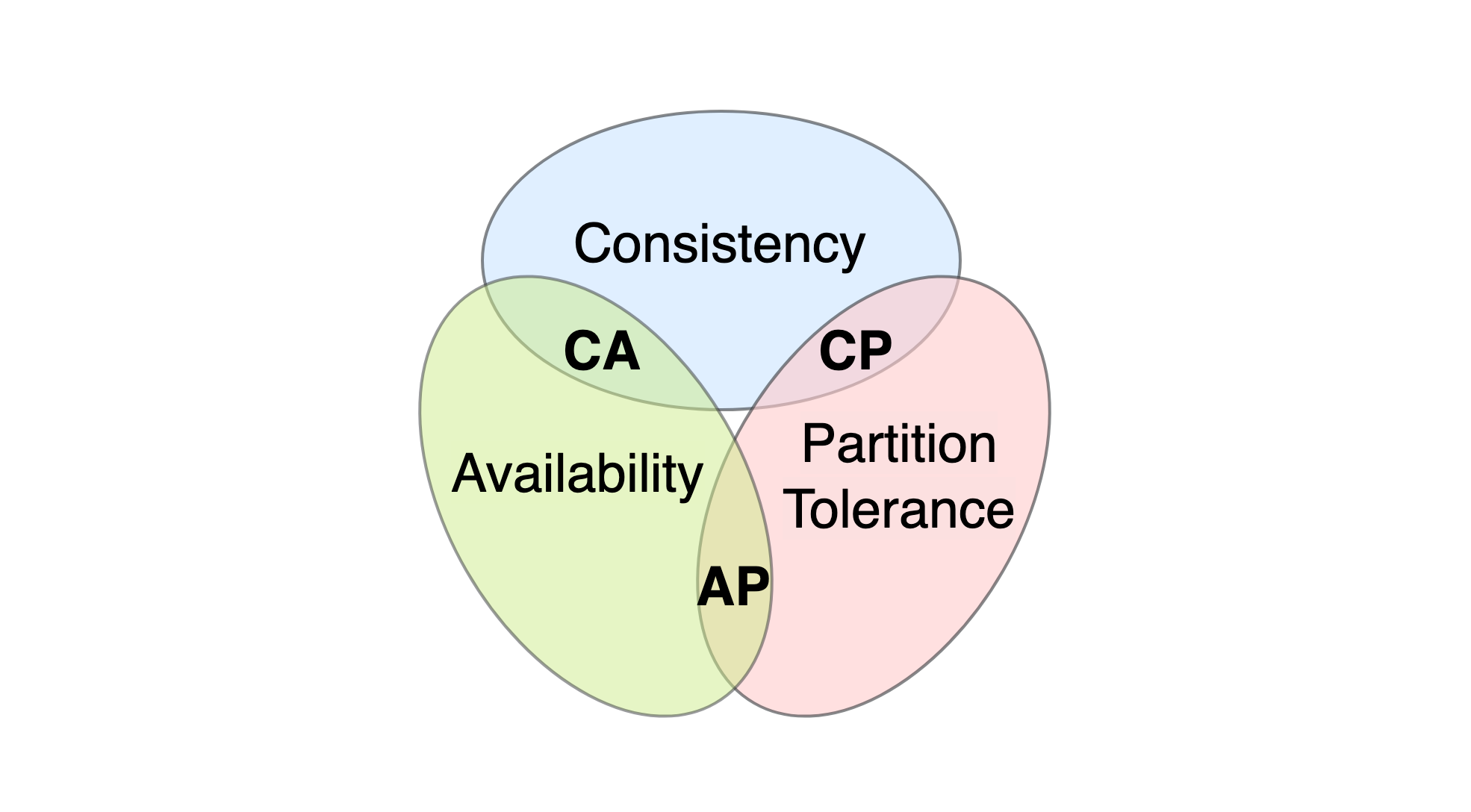
在理论计算机科学中，CAP定理（CAP theorem），又被称作布鲁尔定理（Brewer’s theorem），它指出对于一个分布式计算系统来说，不可能同时满足以下三点：
一致性（Consistency）（等同于所有节点访问同一份最新的数据副本）注意这里和我们数据库一致性是不一样的，前者是副本的一致性，后者最终数据一致性
可用性（Availability）（每次请求都能获取到非错的响应——但是不保证获取的数据为最新数据）
分区容错性（Partition tolerance）（以实际效果而言，分区相当于对通信的时限要求。系统如果不能在时限内达成数据一致性，就意味着发生了分区的情况，必须就当前操作在C和A之间做出选择）
分区容错性（Partition tolerance）
一个分布式系统里面，节点组成的网络本来应该是连通的。然而可能因为一些故障，使得有些节点之间不连通了，整个网络就分成了几块区域。数据就散布在了这些不连通的区域中。这就叫分区。
当你一个数据项只在一个节点中保存，那么分区出现后，和这个节点不连通的部分就访问不到这个数据了。这时分区就是无法容忍的。
提高分区容忍性的办法就是一个数据项复制到多个节点上，那么出现分区之后，这一数据项就可能分布到各个区里。容忍性就提高了。
然而，要把数据复制到多个节点，就会带来一致性的问题，就是多个节点上面的数据可能是不一致的。要保证一致，每次写操作就都要等待全部节点写成功，而这等待又会带来可用性的问题。
总的来说就是，数据存在的节点越多，分区容忍性越高，但要复制更新的数据就越多，一致性就越难保证。为了保证一致性，更新所有节点数据所需要的时间就越长，可用性就会降低。
根据定理，分布式系统只能满足三项中的两项而不可能满足全部三项。
理解CAP理论的最简单方式是想象两个节点分处分区两侧。允许至少一个节点更新状态会导致数据不一致，即丧失了C性质。如果为了保证数据一致性，将分区一侧的节点设置为不可用，那么又丧失了A性质。除非两个节点可以互相通信，才能既保证C又保证A，这又会导致丧失P性质。
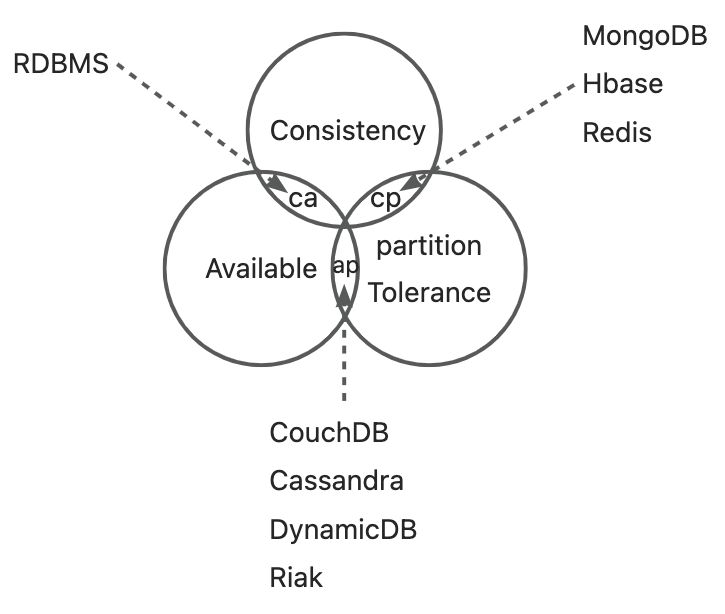
而由于网络硬件肯定会出现延迟丢包等问题，所以分区容错性是我们必须需要实现的。所以我们只能在一致性和可用性之间进行权衡
