数据结构-Binary Indexed Tree 树状数组

152_0.png

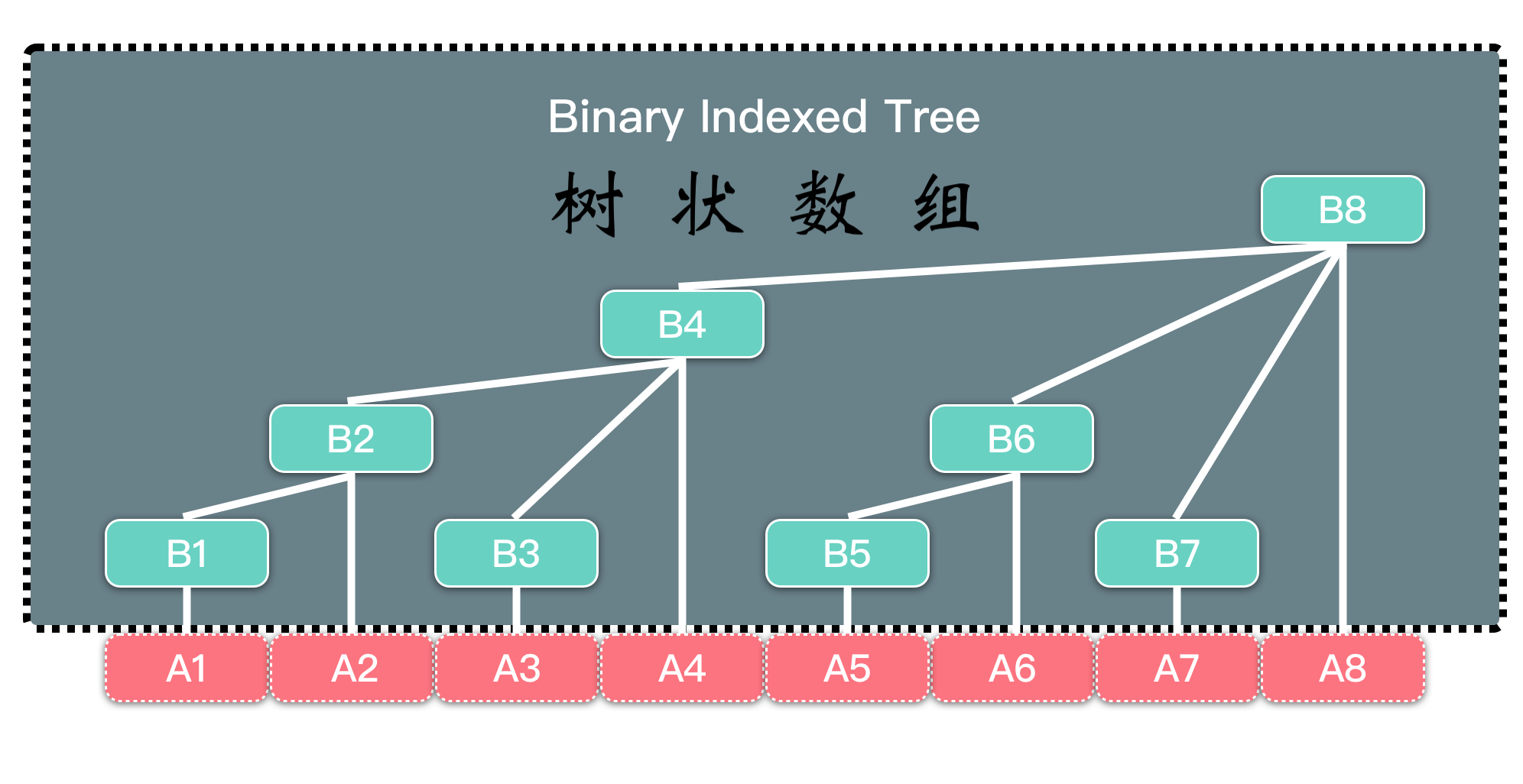
简介

树状数组或二叉索引树（英语：Binary Indexed Tree），又以其发明者命名为Fenwick树，最早由Peter M. Fenwick于1994年以A New Data Structure for Cumulative Frequency Tables为题发表在SOFTWARE PRACTICE AND EXPERIENCE。其初衷是解决数据压缩里的累积频率（Cumulative Frequency）的计算问题，现多用于高效计算数列的前缀和， 区间和。

它的功能是：

  • 单点更新 update(i, v)： 把序列 i_ _位置的数加上一个值 v
  • 区间查询 query(i)： 查询序列 [1… i] 区间的区间和，即 i_ _位置的前缀和

修改和查询的时间代价都是 O(log n)，其中 n_ _为需要维护前缀和的序列的长度。

image.png
树状数组的主要结构就是父节点存储大范围，子节点再进行划分范围，直到节点为一个。
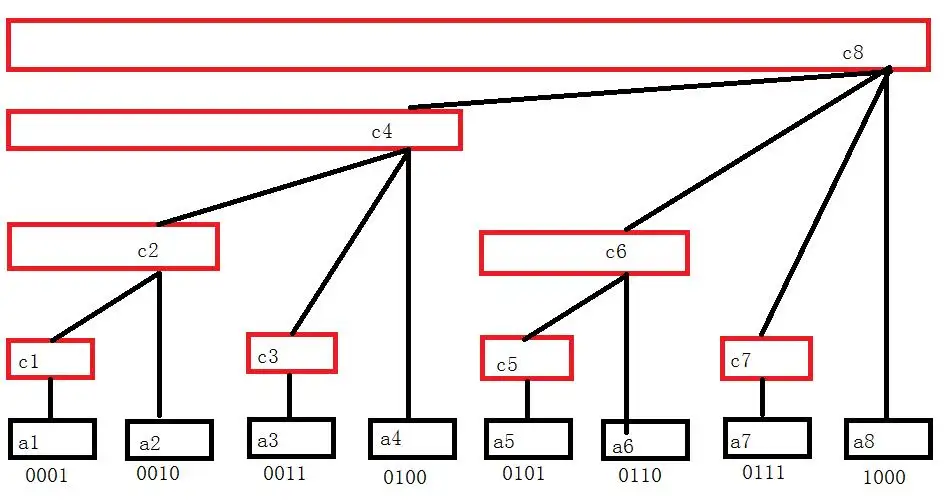
c8表示整个数组，其子节点为c4，c6，c7，a8，各自子节点又有自己的子节点。如果要求数组a的区间和，比如说 [a5,a7] 区间，从[0，a7]中求和，然后减去和从[0，a4]中查找和。

树状数组和线段树具有相似的功能，还有一些区别：

树状数组能有的操作，线段树一定有；线段树有的操作，树状数组不一定有。但是树状数组的代码要比线段树短，思维更清晰，速度也更快，在解决一些单点修改的问题时，树状数组是不二之选。可以理解为树状数组是线段树的精简版。

那么怎么知道表示的是哪个区间呢?这时我们引入一个函数lowbit

1
2
3
4
5
6
7
8
public int lowbit(int x) {
  // x 的二进制表示中，最低位的 1 的位置。
  // lowbit(0b10110000) == 0b00010000
  //          ~~~^~~~~
  // lowbit(0b11100100) == 0b00000100
  //          ~~~~~^~~
  return x & -x;//获取最低位的第一个1（最右边）
}

当最低位 1 和后面的 0 组成然后即在十进制是 ，所以 共包含 8 个 a数组中的元素。

使用 lowbit 函数，我们可以实现很多操作，例如单点修改，将加上 ，只需要更新 的所有上级：

1
2
3
4
5
6
public void add(int x, int k) {
  while (x <= n) {  // 不能越界
    c[x] = c[x] + k;
    x = x + lowbit(x);
  }
}

求前缀和

1
2
3
4
5
6
7
8
public int getsum(int x) {  // a[1]..a[x]的和
  int ret = 0;
  while (x >= 1) {
    ret = ret + c[x];
    x = x - lowbit(x);
  }
  return ret;
}

区间求和

在求区间和时我们需要再维护一个差分数组当我们对树状数组的一个前缀 r 求和，即,由差分数组定义得进行推导
所以区间和可以用两个前缀和相减得到，因此只需要用两个树状数组分别维护 和 ，就能实现区间求和。

差分

差分（difference）又名差分函数或差分运算，差分的结果反映了离散量之间的一种变化，是研究离散数学的一种工具。读者熟悉等差数列：，其中d为常数，称为公差， 即 , 这就是一个差分, 通常用来表示，于是有 , 这是一个最简单形式的差分方程。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
int[] t1, t2;
int n;

public int lowbit(int x) { return x & (-x); }

public void add(int k, int v) {
    int v1 = k * v;
    while (k <= n) {
        t1[k] += v;
        t2[k] += v1;
        k += lowbit(k);
    }
}

public int getSum(int[] t, int k) {
    int ret = 0;
    while (k>0) {
        ret += t[k];
        k -= lowbit(k);
    }
    return ret;
}

public void add1(int l, int r, int v) {
    add(l, v);
    add(r + 1, -v);  // 将区间加差分为两个前缀加
}

public long getSum1(int l, int r) {
    return (r + 1) * getSum(t1, r) - 1 * l * getSum(t1, l - 1) - (getSum(t2, r) - getSum(t2, l - 1));
}

框架

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
// 上来先把三个方法写出来
{
    int[] tree;
    int lowbit(int x) {
        return x & -x;
    }
    // 查询前缀和的方法
    int query(int x) {
        int ans = 0;
        for (int i = x; i > 0; i -= lowbit(i)) ans += tree[i];
        return ans;
    }
    // 在树状数组 x 位置中增加值 u
    void add(int x, int u) {
        for (int i = x; i <= n; i += lowbit(i)) tree[i] += u;
    }
}

// 初始化「树状数组」，要默认数组是从 1 开始
{
    for (int i = 0; i < n; i++) add(i + 1, nums[i]);
}

// 使用「树状数组」：
    {   
    void update(int i, int val) {
        // 原有的值是 nums[i]，要使得修改为 val，需要增加 val - nums[i]
        add(i + 1, val - nums[i]); 
        nums[i] = val;
    }
    
    int sumRange(int l, int r) {
        return query(r + 1) - query(l);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class BIT {
    private int[] tree;
    private int n;

    public BIT(int n) {
        this.n = n;
        this.tree = new int[n + 1];
    }

    public static int lowbit(int x) {
        return x & (-x);
    }

    public int query(int x) {
        int ret = 0;
        while (x != 0) {
            ret += tree[x];
            x -= lowbit(x);
        }
        return ret;
    }

    public void update(int x) {
        while (x <= n) {
            ++tree[x];
            x += lowbit(x);
        }
    }
}

应用

Range Update and Range Queries（范围更新和范围查询）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
package io.example.algorithm.tree.bit;

public class BinaryIndexedTree {
    /**
     * 返回arr[0..index]的和
     * @param BITree
     * @param index
     * @return
     */
    public int getSum(int BITree[], int index) {
        int sum = 0;
        //BITree[]中的索引比arr[]中的索引多1
        index = index + 1;
        // 遍历BITree的祖先[索引]
        while (index > 0) {
            //将树的当前元素添加到总和
            sum += BITree[index];
            //在getSum视图中将索引移动到父节点
            index -= index & (-index);
        }
        return sum;
    }
    /**
     * 更新节点
     * @param BITree 树状数组
     * @param n 数组长度
     * @param index 待更新的索引
     * @param val 更新的值
     */
    public void updateBIT(int BITree[], int n, int index, int val) {
        //BITree[]中的索引比arr[]中的索引多1
        index = index + 1;
        //遍历所有祖先并添加val
        while (index <= n) {
            //将“val”添加到双树的当前节点
            BITree[index] += val;
            //在更新视图中将索引更新为父级索引
            index += index & (-index);
        }
    }
    /**
     * 返回 [0, x] 的范围和
     * @param x
     * @param BITTree1
     * @param BITTree2
     * @return
     */
    public int sum(int x, int BITTree1[], int BITTree2[]) {
        return (getSum(BITTree1, x) * x) - getSum(BITTree2, x);
    }


    /**
     * 范围更新,从[l,r]区间
     * @param BITTree1
     * @param BITTree2
     * @param n 
     * @param val 更新的值
     * @param l 开始左区间
     * @param r 结束右区间
     */
    public void updateRange(int BITTree1[], int BITTree2[], int n, int val, int l, int r) {
        //更新BIT1
        updateBIT(BITTree1, n, l, val);
        updateBIT(BITTree1, n, r + 1, -val);
        //更新BIT2
        updateBIT(BITTree2, n, l, val * (l - 1));
        updateBIT(BITTree2, n, r + 1, -val * r);
    }

    /**
     * 范围求和
     * @param l 开始左区间
     * @param r 结束右区间
     * @param BITTree1
     * @param BITTree2
     * @return
     */
    public int rangeSum(int l, int r, int BITTree1[], int BITTree2[]) {
        //从[0，r]中求和，然后减去和
        //从[0，l-1]中查找和
        //[l，r]
        return sum(r, BITTree1, BITTree2) - sum(l - 1, BITTree1, BITTree2);
    }

    /**
     * 构建数组数组
     * @param n 数组长度
     * @return 返回构造好的数组数组
     */
    public int[] constructBITree(int n) {
        //创建BITree[]并将其初始化为0
        int[] BITree = new int[n + 1];
        for (int i = 1; i <= n; i++) BITree[i] = 0;
        return BITree;
    }

    public static void main(String[] args) {
        BinaryIndexedTree binaryIndexedTree = new BinaryIndexedTree();
        int n = 5;
        // 维护两个数组
        int[] BITTree1;
        int[] BITTree2;
        BITTree1 = binaryIndexedTree.constructBITree(n);
        BITTree2 = binaryIndexedTree.constructBITree(n);
        //在[0,4]中的所有元素中添加5
        int l = 0, r = 4, val = 5;
        binaryIndexedTree.updateRange(BITTree1, BITTree2, n, val, l, r);
        //在[2,4]中的所有元素中添加2
        l = 2;
        r = 4;
        val = 10;
        binaryIndexedTree.updateRange(BITTree1, BITTree2, n, val, l, r);
        //从中找出所有元素的总和
        // [1,4]
        l = 1;
        r = 4;
        System.out.print("Sum of elements from [" + l + "," + r + "] is ");
        System.out.print(binaryIndexedTree.rangeSum(l, r, BITTree1, BITTree2) + "\n");
    }
}

案例

剑指 Offer 51. 数组中的逆序对

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
class Solution {
    public int reversePairs(int[] nums) {
        int n = nums.length;
        int ret = 0;
        int[] b = nums.clone();
        Arrays.sort(b);//离散化
        BIT bit = new BIT(n);
        for(int i=n-1;i>=0;i--){
            int v = nums[i];
            //确定其桶下标
            int bucket = idx(b,v)+1;
            ret+=bit.query(bucket-1);
            bit.update(bucket);
        }
        return ret;
    }
    //二分搜索离散化后的x所属的桶
    private int idx(int[] a, int x) {
        int left = 0, right = a.length;
        while (left < right) {
            int mid = left + (right - left) / 2;
            if (a[mid] < x) left = mid + 1;
            else right = mid;
        }
        return left;
    }
    class BIT {
        private int[] tree;
        private int n;

        public BIT(int n) {
            this.n = n;
            this.tree = new int[n + 1];
        }

        public static int lowbit(int x) {
            return x & (-x);
        }

        public int query(int x) {
            int ret = 0;
            while (x != 0) {
                ret += tree[x];
                x -= lowbit(x);
            }
            return ret;
        }

        public void update(int x) {
            while (x <= n) {
                ++tree[x];
                x += lowbit(x);
            }
        }
    }
}

315. 计算右侧小于当前元素的个数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
class Solution {
    public List<Integer> countSmaller(int[] nums) {
        int n = nums.length;
        LinkedList<Integer> ret = new LinkedList<>();
        int[] b = nums.clone();
        Arrays.sort(b);//离散化
        BIT bit = new BIT(n);
        for(int i=n-1;i>=0;i--){
            int v = nums[i];
            //确定其桶下标
            int bucket = idx(b,v)+1;
            int cnt =bit.query(bucket-1);
            ret.addFirst(cnt);
            bit.update(bucket);
        }
        return ret;
    }
    //二分搜索离散化后的x所属的桶
    private int idx(int[] a, int x) {
        int left = 0, right = a.length;
        while (left < right) {
            int mid = left + (right - left) / 2;
            if (a[mid] < x) left = mid + 1;
            else right = mid;
        }
        return left;
    }
    class BIT {
        private int[] tree;
        private int n;

        public BIT(int n) {
            this.n = n;
            this.tree = new int[n + 1];
        }

        public static int lowbit(int x) {
            return x & (-x);
        }

        public int query(int x) {
            int ret = 0;
            while (x != 0) {
                ret += tree[x];
                x -= lowbit(x);
            }
            return ret;
        }

        public void update(int x) {
            while (x <= n) {
                ++tree[x];
                x += lowbit(x);
            }
        }
    }
}

6198. 满足不等式的数对数目

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
class Solution {
    //nums1[i] - nums1[j] <= nums2[i] - nums2[j] + diff
    //移项
    //nums1[i] - nums2[i] <= nums1[j] - nums2[j] + diff
    //令 a[i] = nums1[i] - nums2[i]
    //则 a[i] <= a[j] + diff
    //从左到右遍历 a 统计每一个 a[i] <= a[j] + diff (i<j) 的个数即是答案（时间复杂度O(n^2)无法通过）
    //思考如何降低时间复杂度,如果我们知道暴力搜索当前答案的时候是遍历每一个a[i],再遍历 a[j] + diff (i<j) 是否大于 a[i]
    //如果我们能直接知道 当前 i 的右边有多少个大于 a[i]-diff 那我们的时间复杂度就可以降成O(n)了

    //使用桶来记录数的出现次数，从后向前遍历，当遍历到a[i],求得后缀和，即可知道比a[i]大的数的个数

    //     nums1 = [5,2,4,2,3,5,3,7,4,6,5], nums2 = [4,0,0,1,-1,0,0,0,2,3,0], diff = 0
    //         a = [1,2,4,1,3,5,3,7,2,3,5]
    //     index = [0,1,2,3,4,5,6,7,8,9]

    //a[9]=5 vlaue=[0,0,0,0,0,1,0,0,0,0] cnt = 0
    //a[8]=3 vlaue=[0,0,0,1,0,1,0,0,0,0] cnt = 1 (比3大的目前只有5，所以cnt=1)
    //a[7]=2 vlaue=[0,0,1,1,0,1,0,0,0,0] cnt = 2 (比2大的目前有3、5，所以cnt=1+1=2(后缀和))
    //a[6]=7 vlaue=[0,0,1,1,0,1,0,1,0,0] cnt = 0
    //...    
    //a[0]=1 vlaue=[0,2,2,2,1,2,0,1,0,0] cnt = 8

    //所以这个过程的操作很适合使用树状数组来操作

    //树状数组
    //特性：
    //1.单点更新 update(i, v)： 把序列 i 位置的数加上一个值 v，这题 v = 1
    //2.区间查询 query(i)： 查询序列 [1⋯i] 区间的区间和，即 i 位置的前缀和

    //如何确定桶的数量呢，当数组的值很大时，我们不可能开那么多的桶，所以对数组a进行离散化即可    

    public long numberOfPairs(int[] a, int[] nums2, int diff) {
        int n = a.length;
        long ret = 0;
        for(int i=0;i<n;i++)a[i]-=nums2[i];
        int[] b = a.clone();
        Arrays.sort(b);//离散化
        BIT bit = new BIT(n);
        for(int v:a){
            //确定其桶下标
            int bucket = idx(b,v+diff+1);//数组数组+1会更好处理
            ret+=bit.query(bucket);
            bit.update(idx(b,v)+1);
        }
        return ret;
    }
    //二分搜索离散化后的x所属的桶
    private int idx(int[] a, int x) {
        int left = 0, right = a.length;
        while (left < right) {
            int mid = left + (right - left) / 2;
            if (a[mid] < x) left = mid + 1;
            else right = mid;
        }
        return left;
    }

    class BIT {
        private int[] tree;
        private int n;

        public BIT(int n) {
            this.n = n;
            this.tree = new int[n + 1];
        }

        public static int lowbit(int x) {
            return x & (-x);
        }

        public int query(int x) {
            int ret = 0;
            while (x != 0) {
                ret += tree[x];
                x -= lowbit(x);
            }
            return ret;
        }

        public void update(int x) {
            while (x <= n) {
                ++tree[x];
                x += lowbit(x);
            }
        }
    }
}

资料

可视化 ：https://visualgo.net/zh/segmenttree?slide=1

https://www.geeksforgeeks.org/binary-indexed-tree-range-update-range-queries/?ref=gcse
https://www.geeksforgeeks.org/binary-indexed-tree-or-fenwick-tree-2/?ref=gcse

数据结构
#树状数组
数据结构-Binary Indexed Tree 树状数组
https://mikeygithub.github.io/2022/08/13/yuque/数据结构-Binary Indexed Tree 树状数组/
作者
Mikey
发布于
2022年8月13日
许可协议