数据结构-Segment Tree 线段树

image.png

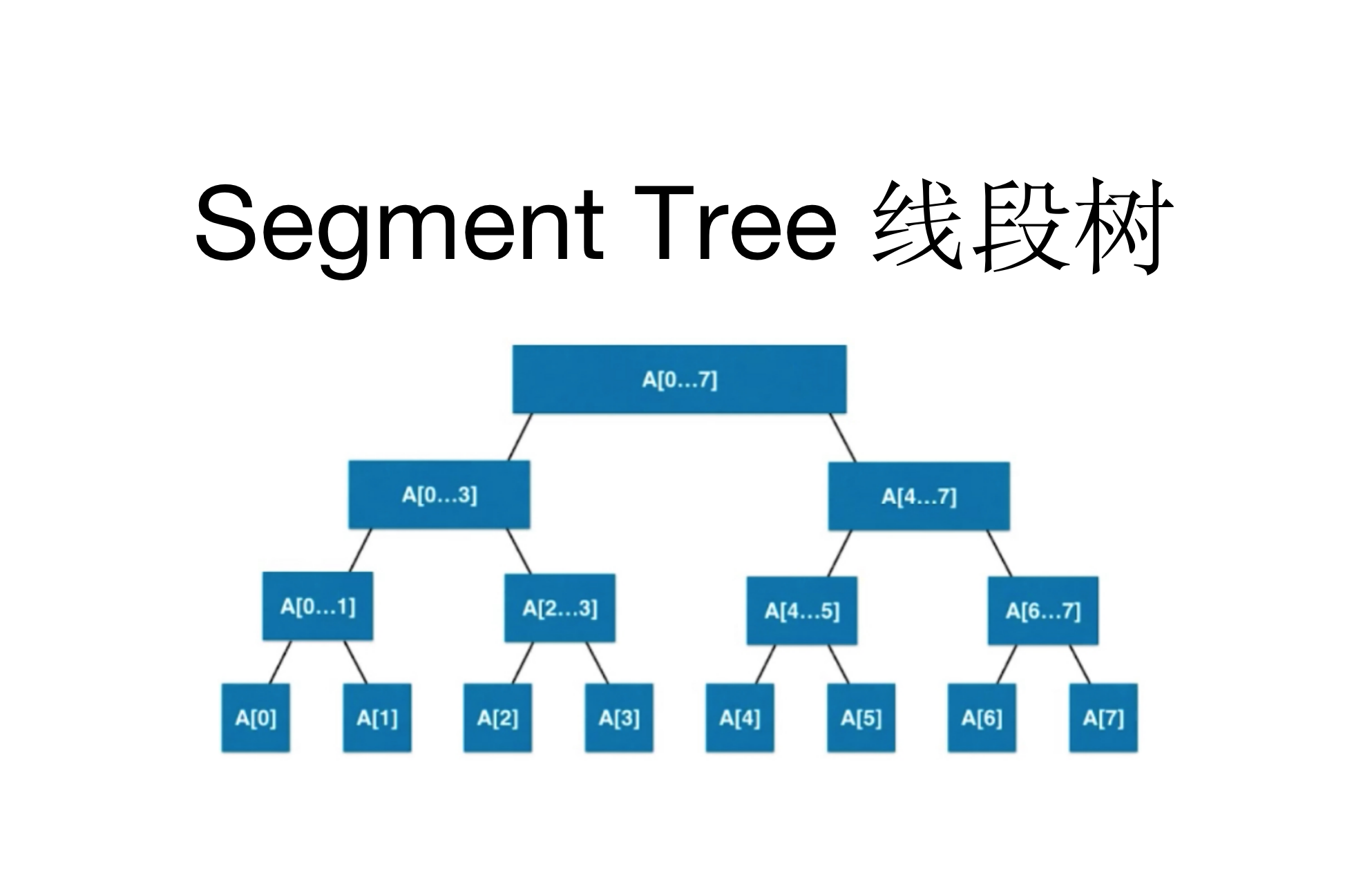
简介

线段树（Segment Tree）主要用于维护区间信息（要求满足结合律）。与树状数组相比，它可以实现 O(logn)的区间修改，还可以同时支持多种操作（加、乘），更具通用性。

image.png

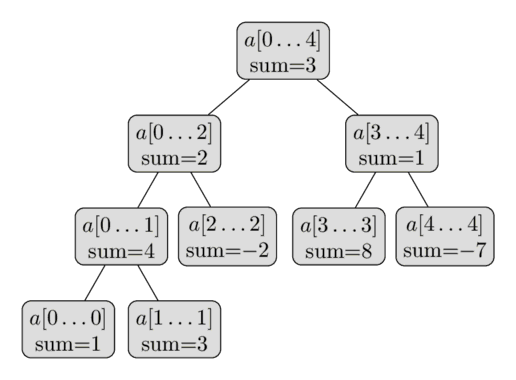
应用

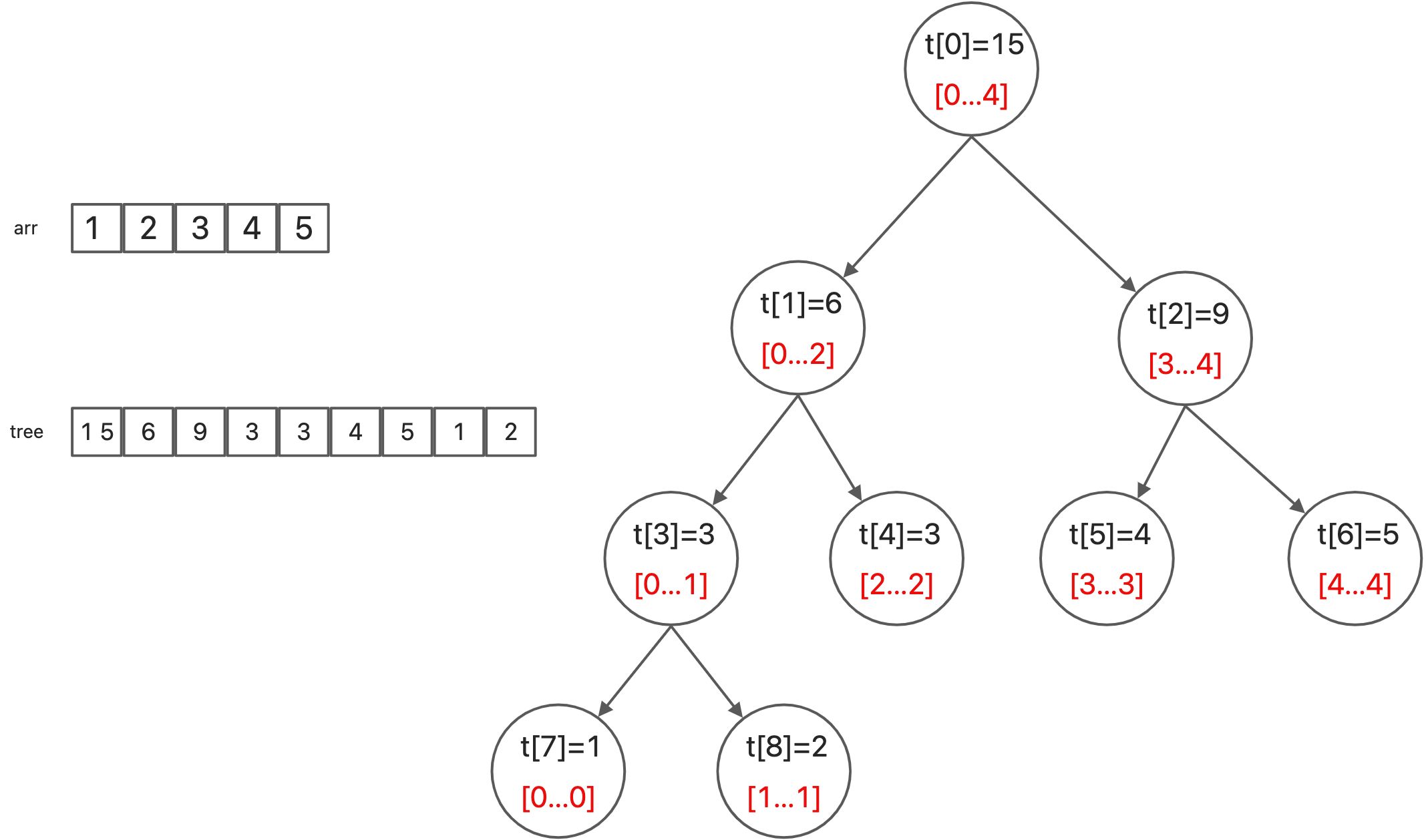
线段树 segmentTree 是一个二叉树，每个结点保存数组 nums 在区间 [s,e] 的最小值、最大值或者总和等信息。线段树可以用树也可以用数组（堆式存储）来实现。对于数组实现，假设根结点的下标为 0，如果一个结点在数组的下标为 node，那么它的左子结点下标为 node×2+1，右子结点下标为 node×2+2。

[s,e] =>[start,end]

创建

线段树的创建通过给定的数组开辟一个四倍数组来存储（参考二叉堆），左子结点下标为 node×2+1，右子结点下标为 node×2+2，递归构建。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public class SegmentTree {

    private int[] segmentTree;
    private int n;

    public SegmentTree(int[] nums) {
        n = nums.length;
        segmentTree = new int[nums.length * 4];//一般需要4倍数组大小
        build(0, 0, n - 1, nums);//构建线段树
    }
    //[1, 2, 3, 4, 5]
    //[15, 6, 9, 3, 3, 4, 5, 1, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
    private void build(int node, int s, int e, int[] nums) {
        if (s == e) {// 如果 start==end 那递归结束，当前区间只有一个数(节点),segmentTree[node] = nums[s]
            segmentTree[node] = nums[s];
            return;
        }
        int m = s + (e - s) / 2;//取中点（防止溢出）
        build(node * 2 + 1, s, m, nums);//构建左子树
        build(node * 2 + 2, m + 1, e, nums);//构建右子树
        segmentTree[node] = segmentTree[node * 2 + 1] + segmentTree[node * 2 + 2];//当前数节点
    }
}

关于线段树的空间：如果采用堆式存储（ 2p是 p 的左儿子，2p+1 是 p 的右儿子），若有 m 个叶子结点，则 d 数组的范围最大为 。
分析：容易知道线段树的深度是 的，则在堆式储存情况下叶子节点（包括无用的叶子节点）数量为 个，又由于其为一棵完全二叉树，则其总节点个数 。当然如果你懒得计算的话可以直接把数组长度设为 4n，因为 的最大值在 时取到，此时节点数为4n 。

更新

更新节点主要是递归+二分（根据下标）查找指定的节点，将其替换为最新值，递归更新其父节点即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public void update(int index, int val) {
    change(index, val, 0, 0, n - 1);
}
private void change(int index, int val, int node, int s, int e) {
    if (s == e) {//递归结束（查找到对应的下标）
        segmentTree[node] = val;//更新最新值
        return;
    }
    int m = s + (e - s) / 2;//获取中点
    if (index <= m) {//如果m>=index说明在左边区间
        change(index, val, node * 2 + 1, s, m);
    } else {//否则在右边区间
        change(index, val, node * 2 + 2, m + 1, e);
    }
    //更新父节点
    segmentTree[node] = segmentTree[node * 2 + 1] + segmentTree[node * 2 + 2];
}

求和

根据指定的下标left、right求该区间arr[left…right]的数据和。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
public int sumRange(int left, int right) {
    return range(left, right, 0, 0, n - 1);
}

/**
 * 范围求和 range 函数
 * 给定区间 [left,right] 时，我们将区间 [left,right] 拆成多个结点对应的区间。
 * 如果结点 node 对应的区间与 [left,right] 相同，可以直接返回该结点的值，即当前区间和。
 * 如果结点 node 对应的区间与 [left,right] 不同，设左子结点对应的区间的右端点为 m，那么将区间 [left,right] 沿点 m 拆成两个区间，分别计算左子结点和右子结点。
 * 我们从根结点开始递归地拆分区间 [left,right]
 *
 * @param left 目标范围左索引
 * @param right 目标范围右索引
 * @param node 当前索引
 * @param s 开始左区间
 * @param e 结束右区间
 * @return 返回[left,right]数值之和
 */
private int range(int left, int right, int node, int s, int e) {
    //（递归结束）没有重叠范围，返回当前节点
    if (left == s && right == e) return segmentTree[node];
    int m = s + (e - s) / 2;//获取中点
    if (right <= m) {//如果right <= m说明[left,right]在全部左区间
        return range(left, right, node * 2 + 1, s, m);
    } else if (left > m) {//如果right <= m说明[left,right]在全部在右区间
        return range(left, right, node * 2 + 2, m + 1, e);
    } else {//否则[left,right]有部分在左区间有部分在右区间，把两者相加即可
        return range(left, m, node * 2 + 1, s, m) + range(m + 1, right, node * 2 + 2, m + 1, e);
    }
}

特性

线段树的惰性传播 (Lazy Propagation in Segment Tree)

惰性传播 (Lazy Propagation in Segment Tree)很多地方又叫做【懒标记】

当我们对某个区间 [left,right] 值进行修改时需要遍历 [left,right]所有节点进行更新。在这种情况引入【懒标记】可以有效降低复杂度。

懒标记：每次执行修改操作时，通过打标记的方式表明该节点对应的区间在某一次操作中被更改，但不更新该节点的子节点信息。正在的修改在下一次访问带有标记的节点时才进行。


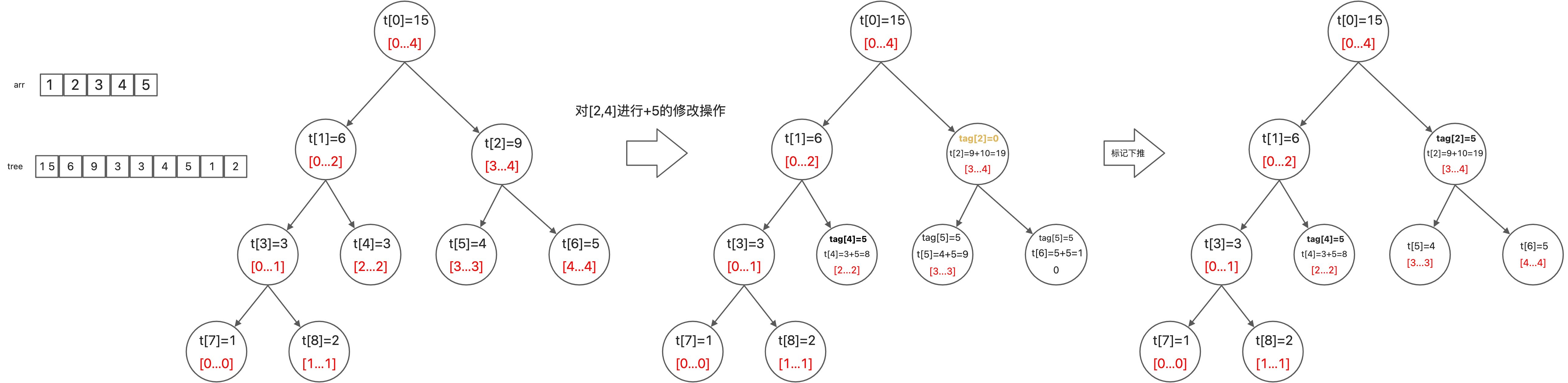
对 [2,4] 区间的每个节点进行 +5 的修改操作，可知 [2,4] 包含的节点共有 [2…2], [3…3], [4…4] 共三个节点，其中 [3…3], [4…4] 属于 t[2] 的子节点所以我们可以直接在 t[2] 打上一个懒标记 tag[2] = 5,不对其子节点进行改动，但不影响查询结果。

那什么时候进行更新其子节点呢？当我们进行查询 [3,4] 区间范围和时，发现 [3,4] 区间还存在有懒标记，此时对懒标记进行下放，更新节点值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
package io.example.algorithm.tree.segmenttree;

class LazySegmentTree {

    final int MAX = 1000;     // 树的最大节点
    int tree[] = new int[MAX]; // 存储树节点
    int lazy[] = new int[MAX]; // 存储节点懒标记值

    /**
     * 更新给定范围的值
     * @param curSegmentIndex 线段树中当前节点的索引
     * @param segmentStart 当前节点存储和的元素的开始索引
     * @param segmentEnd 当前节点存储和的元素的结束索引
     * @param updateStart 更新的开始索引
     * @param updateEnd 更新的结束索引
     * @param diff 更新的值
     */
    void updateRangeUtil(int curSegmentIndex, int segmentStart, int segmentEnd, int updateStart, int updateEnd, int diff) {
        // 如果段树的当前节点的懒标记值不为零，则存在一些挂起的更新。
        // 因此，我们需要确保在进行新的更新之前完成待定的更新。
        // 因为在递归调用之后，父级可能会使用该值（请参阅此函数的最后一行）
        if (lazy[curSegmentIndex] != 0) {
            // 使用惰性节点中存储的值进行挂起的更新
            tree[curSegmentIndex] += (segmentEnd - segmentStart + 1) * lazy[curSegmentIndex];
            // 检查它是否不是叶节点，因为如果这是叶节点，无需再向下执行
            if (segmentStart != segmentEnd) {
                //我们可以推迟更新孩子们，因为我们现在不需要他们的新价值观。
                //因为我们还没有更新si的子级，所以我们需要为这些子级设置懒惰标志
                lazy[curSegmentIndex * 2 + 1] += lazy[curSegmentIndex];
                lazy[curSegmentIndex * 2 + 2] += lazy[curSegmentIndex];
            }
            //将当前节点的延迟值设置为0表示已经更新
            lazy[curSegmentIndex] = 0;
        }
        // 超出下标，递归结束
        if (segmentStart > segmentEnd || segmentStart > updateEnd || segmentEnd < updateStart) return;
        // 当前段完全在范围内
        if (segmentStart >= updateStart && segmentEnd <= updateEnd) {
            // Add the difference to current node
            // 将差异添加到当前节点
            tree[curSegmentIndex] += (segmentEnd - segmentStart + 1) * diff;
            // 检查叶节点与否的逻辑相同
            if (segmentStart != segmentEnd) {
                // 这是我们在惰性节点中存储值的地方，而不是更新段树本身
                // 因为我们现在不需要这些更新的值，我们通过在lazy[]中存储值来推迟更新
                lazy[curSegmentIndex * 2 + 1] += diff;
                lazy[curSegmentIndex * 2 + 2] += diff;
            }
            return;
        }
        //如果不完全在范围内，但重叠，进入子递归
        int mid = (segmentStart + segmentEnd) / 2;
        updateRangeUtil(curSegmentIndex * 2 + 1, segmentStart, mid, updateStart, updateEnd, diff);
        updateRangeUtil(curSegmentIndex * 2 + 2, mid + 1, segmentEnd, updateStart, updateEnd, diff);
        // 并使用子节点调用的结果更新此节点
        tree[curSegmentIndex] = tree[curSegmentIndex * 2 + 1] + tree[curSegmentIndex * 2 + 2];
    }

    /**
     * 更新函数入口
     * @param n 数组长度
     * @param updateStart 更新的开始下标
     * @param updateEnd 更新的结束下标
     * @param diff 更新的数值
     */
    void updateRange(int n, int updateStart, int updateEnd, int diff) {
        updateRangeUtil(0, 0, n - 1, updateStart, updateEnd, diff);
    }
    
    /**
     * 求区间和
     * @param segmentStart 线段树开始索引
     * @param segmentEnd 线段树结束索引
     * @param queryStart 查询开始索引
     * @param queryEnd 查询结束索引
     * @param curSegmentIndex 当前节点下标
     * @return 返回当前[queryStart,queryEnd]区间和
     */
    int getSum(int segmentStart, int segmentEnd, int queryStart, int queryEnd, int curSegmentIndex) {
        // 如果懒标记不为零需要进行下推
        if (lazy[curSegmentIndex] != 0) {
            // 更新当前节点
            tree[curSegmentIndex] += (segmentEnd - segmentStart + 1) * lazy[curSegmentIndex];
            //检查它是否不是叶节点，因为如果这是叶节点，我们不需要再往下递归
            if (segmentStart != segmentEnd) {
                // 进入子节点递归
                lazy[curSegmentIndex * 2 + 1] += lazy[curSegmentIndex];
                lazy[curSegmentIndex * 2 + 2] += lazy[curSegmentIndex];
            }
            //取消设置当前节点的延迟值/已更新
            lazy[curSegmentIndex] = 0;
        }
        // 超出范围
        if (segmentStart > segmentEnd || segmentStart > queryEnd || segmentEnd < queryStart) return 0;
        // 如果该段位于范围内
        if (segmentStart >= queryStart && segmentEnd <= queryEnd) return tree[curSegmentIndex];
        //如果部分重合
        int mid = (segmentStart + segmentEnd) / 2;
        return getSum(segmentStart, mid, queryStart, queryEnd, 2 * curSegmentIndex + 1) + getSum(mid + 1, segmentEnd, queryStart, queryEnd, 2 * curSegmentIndex + 2);
    }
    
    /**
     * 求和函数入口
     * @param n 数组长度
     * @param queryStart 查询开始下标
     * @param queryEnd 查询结束下标
     * @return 返回当前[queryStart,queryEnd]区间和
     */
    int getSum(int n, int queryStart, int queryEnd) {
        // 检查错误的输入值
        if (queryStart < 0 || queryEnd > n - 1 || queryStart > queryEnd) {
            System.out.println("Invalid Input");
            return -1;
        }
        return getSum(0, n - 1, queryStart, queryEnd, 0);
    }


    /**
     * 构建线段树
     * @param arr 数组
     * @param segmentStart 线段树开始索引
     * @param segmentEnd 线段树结束索引
     * @param curSegmentIndex 当前索引
     */
    void build(int arr[], int segmentStart, int segmentEnd, int curSegmentIndex) {
        // 超出范围，因为start永远不能大于end
        if (segmentStart > segmentEnd) return;
        //start==end只有一个数直接设置值结束递归
        if (segmentStart == segmentEnd) {
            tree[curSegmentIndex] = arr[segmentStart];
            return;
        }
        //递归构建子树
        int mid = (segmentStart + segmentEnd) / 2;
        build(arr, segmentStart, mid, curSegmentIndex * 2 + 1);
        build(arr, mid + 1, segmentEnd, curSegmentIndex * 2 + 2);
        tree[curSegmentIndex] = tree[curSegmentIndex * 2 + 1] + tree[curSegmentIndex * 2 + 2];
    }
    
    /**
     * 构造线段树
     * @param arr
     */
    void build(int arr[]) {
        build(arr, 0, arr.length - 1, 0);
    }
    
    public static void main(String args[]) {
        int arr[] = {1, 3, 5, 7, 9, 11};
        int n = arr.length;
        LazySegmentTree tree = new LazySegmentTree();
        // 构建线段树
        tree.build(arr);
        // 打印下标[1,3]的范围和
        System.out.println("Sum of values in given range = " + tree.getSum(n, 1, 3));
        // 在索引从1到5的所有节点上添加10
        tree.updateRange(n, 1, 5, 10);
        // 更新值后查找总和
        System.out.println("Updated sum of values in given range = " + tree.getSum(n, 1, 3));
    }
}

线段树的区间求和 (Sum of given range)

在给定的区间 [left,right] 范围内如果存在节点的范围恰好是 [left,right] 那直接返回当前节点值即可，否则需要将 [left,right] 切割成两部分递归查找所属范围在求和即可。

如果要查询的区间为 [2,4]，此时就不能直接获取区间的值[2,4]，但是 可以拆成 [2,2] 和 [3,4]，可以通过合并这两个区间的答案来求得这个区间的答案。

带节点更新的范围最大查询 (Range Maximum Query with Node Update)

查询最大值主要是直接获取存储的最大值，当更新时递归的获取当前范围的节点的最大值进行比较进行更新

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
package io.example.algorithm.tree.segmenttree;

class GFG {

    /**
     * 获取[l,r]范围的最大值
     *
     * @param st
     * @param ss
     * @param se
     * @param l
     * @param r
     * @param node
     * @return
     */
    static int MaxUtil(int[] st, int ss, int se, int l, int r, int node) {
        //如果该节点的段完全覆盖给定范围的一部分，直接返回线段的最大值
        if (l <= ss && r >= se) return st[node];
        //如果此节点的段不存在属于给定范围
        if (se < l || ss > r) return -1;
        //如果该节点的部分在给定范围内
        int mid = ss + (se - ss) / 2;
        return Math.max(MaxUtil(st, ss, mid, l, r, 2 * node + 1), MaxUtil(st, mid + 1, se, l, r, 2 * node + 2));
    }

    /**
     * 一个递归函数来更新节点中包含给定索引的节点
     *
     * @param arr   数组
     * @param st    线段树存储数组
     * @param ss    线段树开始索引
     * @param se    线段树结束索引
     * @param index 要更新的元素的索引
     * @param value 更新的值
     * @param node
     */
    static void updateValue(int arr[], int[] st, int ss, int se, int index, int value, int node) {
        if (index < ss || index > se) {
            System.out.println("Invalid Input");
            return;
        }
        if (ss == se) {
            ///更新数组和中的值
            arr[index] = value;
            st[node] = value;
        } else {
            int mid = ss + (se - ss) / 2;
            if (index >= ss && index <= mid) {
                updateValue(arr, st, ss, mid, index, value, 2 * node + 1);
            } else {
                updateValue(arr, st, mid + 1, se, index, value, 2 * node + 2);
            }
            st[node] = Math.max(st[2 * node + 1], st[2 * node + 2]);
        }
        return;
    }

    //返回范围为的最大元素数索引l（查询开始）到r（查询结束）
    static int getMax(int[] st, int n, int l, int r) {

        // 检查错误的输入值
        if (l < 0 || r > n - 1 || l > r) {
            System.out.printf("Invalid Input\n");
            return -1;
        }

        return MaxUtil(st, 0, n - 1, l, r, 0);
    }

    /**
     * 构建线段树
     *
     * @param arr 数组
     * @param ss  线段树开始索引
     * @param se  线段树结束索引
     * @param st  线段树存储数组
     * @param si  当前节点线段树索引
     * @return
     */
    static int build(int arr[], int ss, int se, int[] st, int si) {

        //如果数组中有一个元素，则存储它位于段树的当前节点中并返回
        if (ss == se) {
            st[si] = arr[ss];
            return arr[ss];
        }

        //依次构建左右子树
        int mid = ss + (se - ss) / 2;

        st[si] = Math.max(build(arr, ss, mid, st, si * 2 + 1), build(arr, mid + 1, se, st, si * 2 + 2));

        return st[si];
    }

    /**
     * 构建线段树入口
     *
     * @param arr 数组
     * @param n   长度
     * @return
     */
    static int[] build(int arr[], int n) {
        // 线段树的高度
        int x = (int) Math.ceil(Math.log(n) / Math.log(2));
        // 线段树的最大大小
        int max_size = 2 * (int) Math.pow(2, x) - 1;
        // 分配数组大小
        int[] st = new int[max_size];
        // 构建
        build(arr, 0, n - 1, st, 0);
        // 返回构造的段树
        return st;
    }

    public static void main(String[] args) {
        int[] arr = {1, 3, 5, 7, 9, 11};
        int n = arr.length;
        // 构建线段树
        int[] st = build(arr, n);
        // 获取[1,3]范围最大值
        System.out.println("Max of values in given range = " + getMax(st, n, 1, 3));
        // 更新: 设置 arr[1] = 8
        updateValue(arr, st, 0, n - 1, 1, 8, 0);
        // 找到更新后的最大值
        System.out.println("Updated max of values in given range = " + getMax(st, n, 1, 3));
    }
}

进阶

线段树的高效实现 (Segment Tree Efficient Implementation)

线段树的高效实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
class SegmentTree {
    //线段数（叶子节点都是数组的元素）
    //[1,3,5]       [1,3,5,7]        ......
    //      9           16
    //     / \         /  \
    //    4   5       4    12
    //   / \         / \   / \
    //  1   3       1   3 5   7      ......
    // n=3 node=6   n=4 node=7     n=5 node=9  n=6 node=12  node<=2*n
    int[] tree;
    int n;
    public SegmentTree(int[] nums) {
        n = nums.length;
        tree = new int[2*n];
        buildTree(nums);
    }
    //构建线段树
    public void buildTree(int[] nums){
        //nums=[1,3,5,7] tree = [0,0,0,0,1,3,5,7] 
        //将所有叶子节点放置在[n,2n)数组中
        for (int i = n, j = 0;  i < 2 * n; i++,  j++)tree[i] = nums[j];
        //tree = [0,16,4,12,1,3,5,7] 
        //把父节点放置在[1,n)数组中 , tree[i] = tree[i * 2] + tree[i * 2 + 1]
        for (int i = n - 1; i > 0; --i)tree[i] = tree[i * 2] + tree[i * 2 + 1];
    }
    //更新某个下标同时需要更新其父节点的值
    public void update(int index, int val) {
        index+=n;//下标的位置,n+下标
        tree[index] = val;
        //更新父亲节点,因为tree[i] = tree[i * 2] + tree[i * 2 + 1];所以index如果是奇数则为右子树，index是偶数则为左子树
        while(index>0){
            int left = index;
            int right = index;
            if(index % 2 == 0) right = index+1;
            else left = index - 1;
            //更新父节点值
            tree[index / 2] = tree[left] + tree[right];
            //更新下标
            index /= 2;
        }

    }
    //求和只需要获取其父节点
    public int sumRange(int left, int right) {//left，right为下标
        //确认在数组中的下标
        left+=n;
        right+=n;
        int ret = 0;
        //[1,3,5,7]
        while(left<=right){
            //1.如果left是左子树可以直接取根节点,如果是右子树那只取右节点
            if(left % 2 == 1 ){
                ret+=tree[left];
                left++;
            }
            //2.如果right是右子树可以直接取根节点,如果是左子树那只取左节点
            if(right % 2 == 0 ){
                ret+=tree[right];
                right--;
            }
            left/=2;
            right/=2;
        }
        return ret;
    }
}

采用位运算加速

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
package io.example.algorithm.tree;

//线段数（叶子节点都是数组的元素）
//   [1,3,5]    [1,3,5,7]        ......
//      9           16
//     / \         /  \
//    4   5       4    12
//   / \         / \   / \
//  1   3       1   3 5   7      ......
// n=3 node=5   n=4 node=7   n=5 node=9  n=6 node=12  node<=2*n
public class SegmentTree {

    // 设置数组的最大值
    int N = 100000;
    int n; //节点个数
    // 设置数组的最大值
    int[] tree = new int[2 * N];

    //                                           |--------|
    //                                           |       +-+
    // 构建线段树                                  v       | |
    //[1,3,5,7] -> [0,0,0,0][1,3,5,7] -> [0,16,4,12][1,3,5,7]
    //                                         ^     | |
    //                                         |     +-+
    //                                         |------|
    void buildTree(int[] arr) {
        // [n,2n)按照顺序存储节点
        for (int i = 0; i < n; i++) tree[n + i] = arr[i];
        // 构建父节点(0,n) 父节点等于 tree[i] = tree[i * 2] + tree[i * 2 + 1];
        for (int i = n - 1; i > 0; --i) tree[i] = tree[i << 1] + tree[i << 1 | 1];
    }

    /**
     * 更新树节点
     * @param p 下标
     * @param value 值
     */
    void updateTreeNode(int p, int value) {
        // 直接更新值
        tree[p + n] = value;
        p = p + n;
        // 同时需要更新其父亲节点
        for (int i = p; i > 1; i = i / 2) tree[i / 2] = tree[i] + tree[i ^ 1];
        for (int i = p; i > 1; i >>= 1) tree[i >> 1] = tree[i] + tree[i ^ 1];
    }

    // function to get sum on
    // interval [l, r)
    int query(int l, int r) {
        int res = 0;
        // loop to find the sum in the range
        // for (l += n, r += n; l < r; l = l / 2, r = r / 2) {
        for (l += n, r += n; l < r; l >>= 1, r >>= 1) {
            if ((l & 1) > 0) res += tree[l++];
            if ((r & 1) > 0) res += tree[--r];
        }
        return res;
    }

    public static void main(String[] args) {
        SegmentTree segmentTree = new SegmentTree();
        int[] a = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12};
        // n is global
        segmentTree.n = a.length;
        // 构建数
        segmentTree.buildTree(a);
        // print the sum in range(1,2)
        // index-based
        System.out.println(segmentTree.query(1, 3));
        // modify element at 2nd index
        segmentTree.updateTreeNode(2, 1);
        // print the sum in range(1,2)
        // index-based
        System.out.println(segmentTree.query(1, 3));
    }
}

资料

https://oi-wiki.org/ds/seg/
https://cp-algorithms.com/data_structures/segment_tree.html
可视化 ：https://visualgo.net/zh/segmenttree?slide=1
给定范围之和：https://www.geeksforgeeks.org/segment-tree-set-1-sum-of-given-range/?ref=gcse
在线段树中懒标记：https://www.geeksforgeeks.org/lazy-propagation-in-segment-tree/?ref=gcse
线段树的高效实现：https://www.geeksforgeeks.org/segment-tree-efficient-implementation/?ref=lbp

数据结构
#线段树
数据结构-Segment Tree 线段树
https://mikeygithub.github.io/2022/04/19/yuque/数据结构-Segment Tree 线段树/
作者
Mikey
发布于
2022年4月19日
许可协议