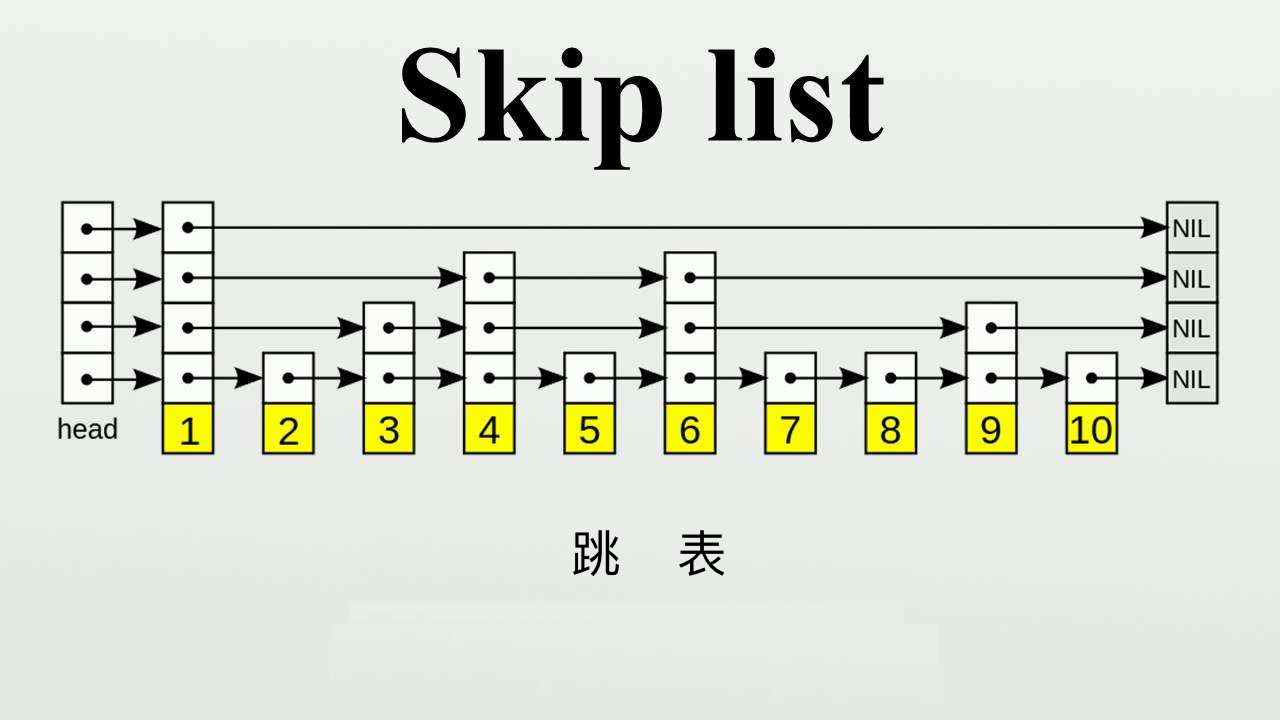
背景
跳表其实是基于排序链表进行建立每一层和段索引的一种数据结构,包括但不限于redis、lucene都有采用的跳表的数据结构来存储数据。
在了解跳表之前我们需要知道链表,链表也是一种常用的数据结构,其节点主要的结构是由节点值+下一个节点的指针组成。
结构体
1
2
3
4
| class Node{
int val;
Node next;
}
|
跳表
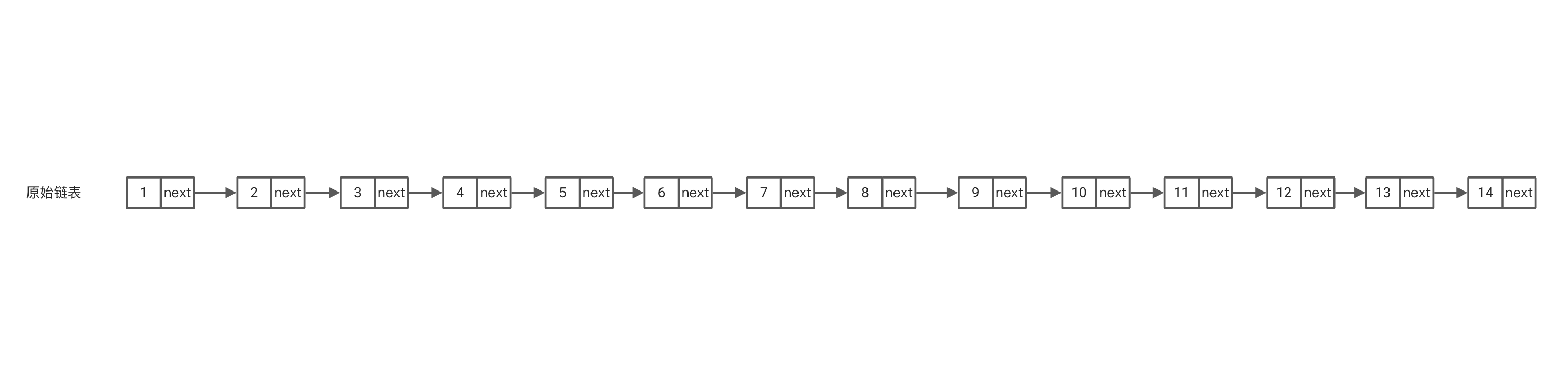
基于上面的链表当我们需要查询链表中是否存在某个数值的时候我们需要不断的遍历这个链表,判断链表的值是否是目标值,其时间复杂度是O(n)。
基于上面的情况,在原有链表的基础上添加一层索引,当需要查找8的节点时,先从索引开始查找1-3-5-7,当遍历到索引的节点值为9时大于8,可知需要查找的节点必定在7-9区间,所以通过索引节点7获取原始链表的节点进行遍历,即在7的下一个节点找到目标值,路径为1-3-5-7-8。
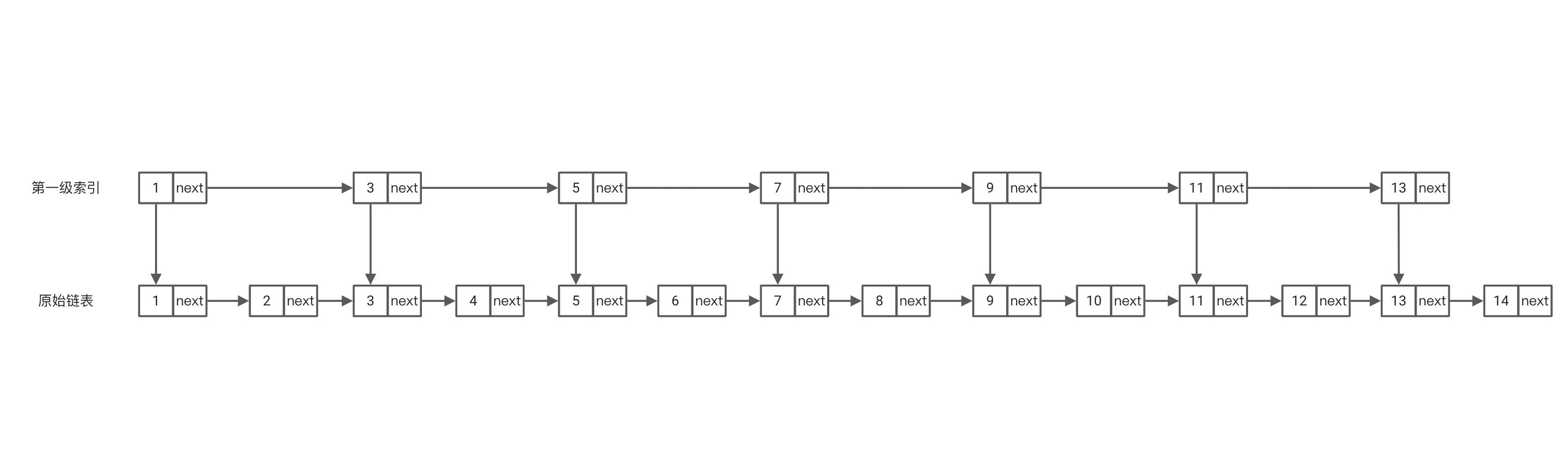
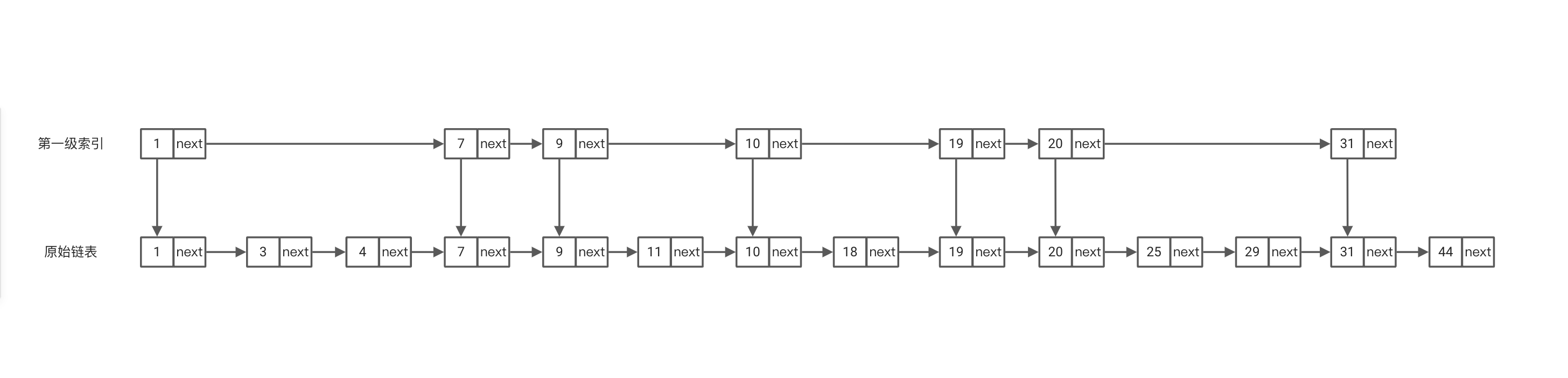
在上面的简单案例中,发现当我们在索引上进行查找时,还是需要遍历1,3,5,这几个目标值不在的区间索引,那么我们如何加速它呢?没错我们可以在第一级索引的基础上再加几层索引,如下
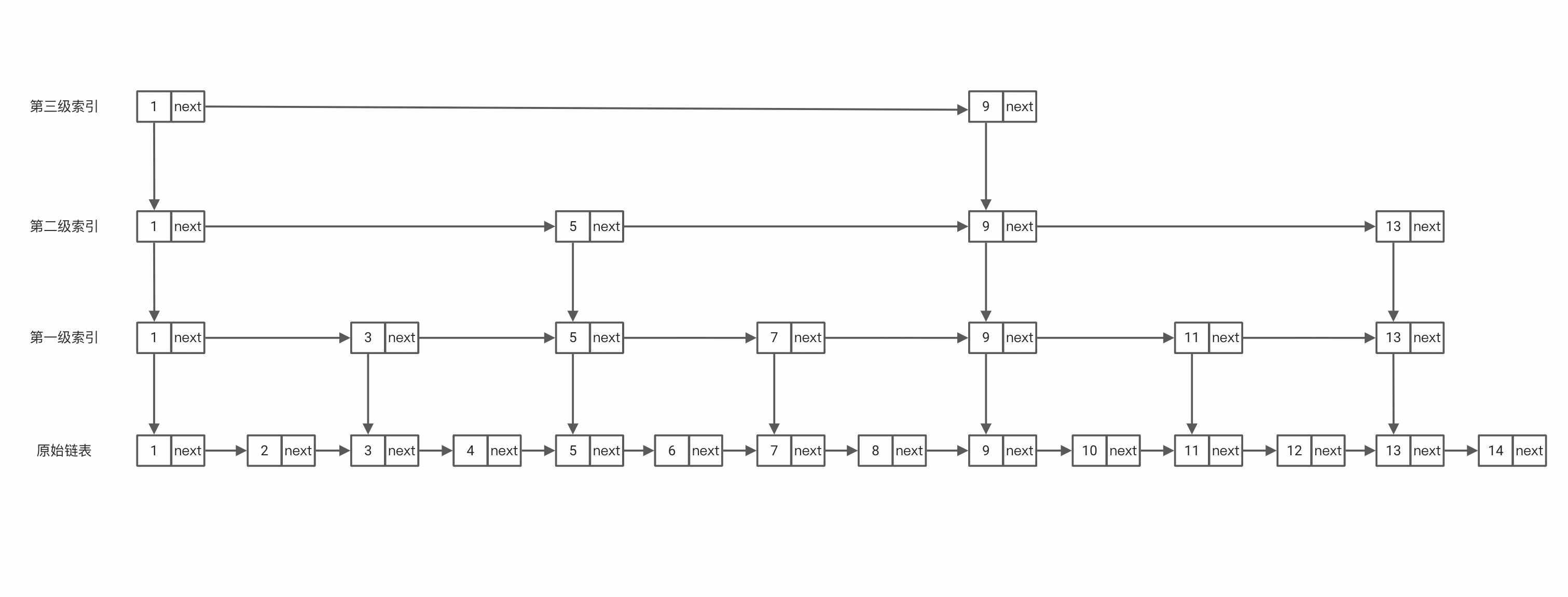
此时我们查找8的执行顺序为1-5-7-8,进一步缩短了我们的查找次数。在当前的节点个数比较少没能体现出其缩短的量,当节点数量级很大的时候就会体现出。
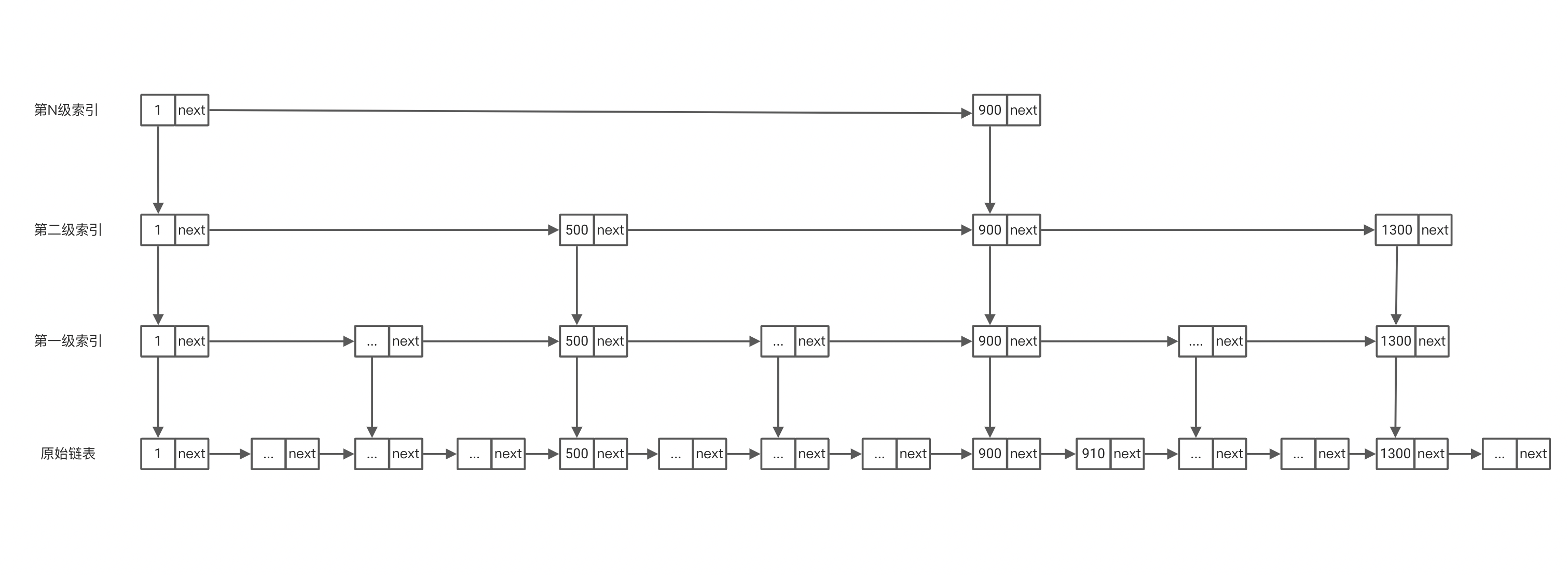
说了这么多其实上面我们说的这种结果就是跳表,其主要的思想是以空间换时间,通过建立多层索引来分割原始链表方便快速确定查找的目标数所在区间。有没有觉得和二分有几分相似呢?
构建
1.首先在跳表中有两种数据结构组成,分别是索引(只存储key)和节点(原始链表)在这里我们暂且是呀同一种结构体
1
2
3
4
| class Node{
Integer value;
Node[] next;
}
|
插入
当需要插入新的元素的时候我们同样通过查找索引的方式定位到我们需要插入的位置,将其插入正确的位置,使其原始链表依旧保持有序,其操作依旧是O(log(n))
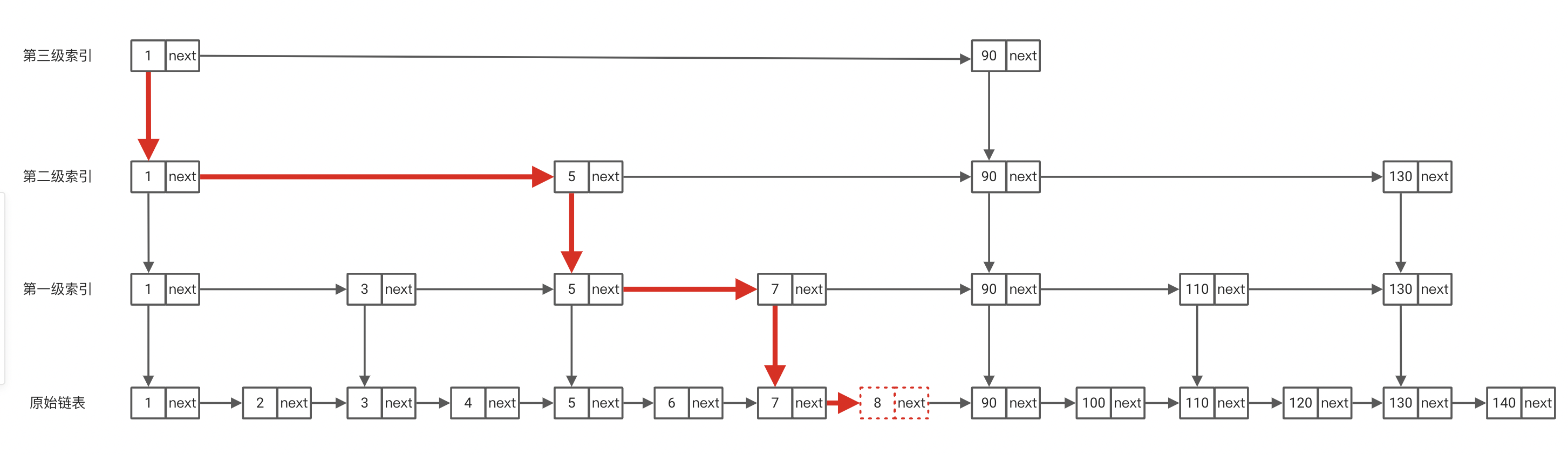
但是我们的元素很多的时候,如下图,此时我们的索引没有更新,其区间7-90就存在很多元素,跳表退化成链表,当我们需要查询89这个目标值的时候,就需要遍历链表7-8-9-…-87,极大的降低了查询的效率。这时候有的同学可能会说,那我没插入一个新的元素我就把跳表的索引进行删掉再重新建立那不就行了?
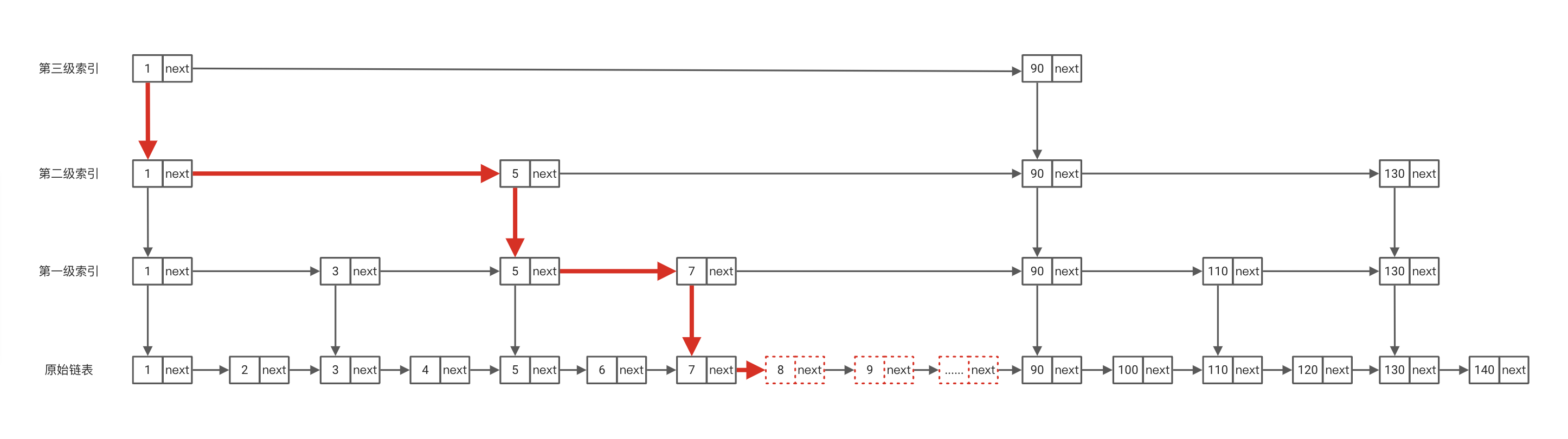
确实是可以每次插入进行重建索引,但是我们知道当我们的链表元素有n个时,其索引的个数是O(n),每当我们进行插入一个元素此时我们划分的时间/空间复杂度都是O(n)。
那有没有其他更加高效的方法来让我们更新索引呢?
我们先来看一下我们的跳表索引,不难看出其实如果基于原始链表每隔一个节点建立一个索引,再层层递推到最高层索引是最理想的。那我们是否可以在原始链表中随机抽出 n/2个节点来作为第一层索引呢?当然可以,当我们的链表节点具有一定量的时候随机本身分布是比较均匀的。随机选 n/2 个元素做为一级索引、随机选 n/4 个元素做为二级索引、随机选 n/8 个元素做为三级索引,依次类推,一直到最顶层索引。这里每层索引的元素个数已经确定,且每层索引元素选取的足够随机,所以可以通过索引来提升跳表的查找效率。
那么这里的随机该如何实现,才能使跳表满足上述这个样子呢?可以在每次新插入元素的时候,让该元素有 1/2 的几率建立一级索引、1/4 的几率建立二级索引、1/8 的几率建立三级索引,以此类推,就能满足我们上面的条件。现在我们就需要一个概率算法帮我们把控这个 1/2、1/4、1/8 … ,当每次有数据要插入时,先通过概率算法告诉我们这个元素需要插入到几级索引中,然后开始维护索引并把数据插入到原始链表中。

redis的随机函数采用位运算加速计算效率
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
private static int DEFAULT_MAX_LEVEL = 32;
private static double DEFAULT_P_FACTOR = 0.25;
private static int randomLevel(){
int level = 1;
while (Math.random()<DEFAULT_P_FACTOR && level<DEFAULT_MAX_LEVEL)level ++ ;
return level;
}
|
在上面的生成的随机层函数中,假如你插入的节点返回的随机层数是5,表示你需要为当前节点建立四级索引,分别是第一级,第二级,第三级,第四级和插入原始链表中。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
| package io.example.algorithm.design;
public class SkipList {
private static int DEFAULT_MAX_LEVEL = 32;
private static double DEFAULT_P_FACTOR = 0.25;
Node head = new Node(null, DEFAULT_MAX_LEVEL);
int currentLevel = 1;
public boolean search(int target) {
Node searchNode = head;
for (int i = currentLevel - 1; i >= 0; i--) {
searchNode = findClosest(searchNode, i, target);
if (searchNode.next[i] != null && searchNode.next[i].value == target) {
return true;
}
}
return false;
}
public void add(int num) {
int level = randomLevel();
Node updateNode = head;
Node newNode = new Node(num, level);
for (int i = currentLevel - 1; i >= 0; i--) {
updateNode = findClosest(updateNode, i, num);
if (i < level) {
if (updateNode.next[i] == null) {
updateNode.next[i] = newNode;
} else {
Node temp = updateNode.next[i];
updateNode.next[i] = newNode;
newNode.next[i] = temp;
}
}
}
if (level > currentLevel) {
for (int i = currentLevel; i < level; i++) {
head.next[i] = newNode;
}
currentLevel = level;
}
}
private Node findClosest(Node node, int levelIndex, int value) {
while ((node.next[levelIndex]) != null && value > node.next[levelIndex].value) {
node = node.next[levelIndex];
}
return node;
}
private static int randomLevel() {
int level = 1;
while (Math.random() < DEFAULT_P_FACTOR && level < DEFAULT_MAX_LEVEL) level++;
return level;
}
class Node {
Integer value;
Node[] next;
public Node(Integer value, int size) {
this.value = value;
this.next = new Node[size];
}
@Override
public String toString() {
return String.valueOf(value);
}
}
}
|
查找
时间复杂度(O(log(n))
查找的操作较为简单,我们先从顶层索引进行查找,确定其目标数所在的区间,再进行索引下推,最终定位到原始链表上再进行查找。
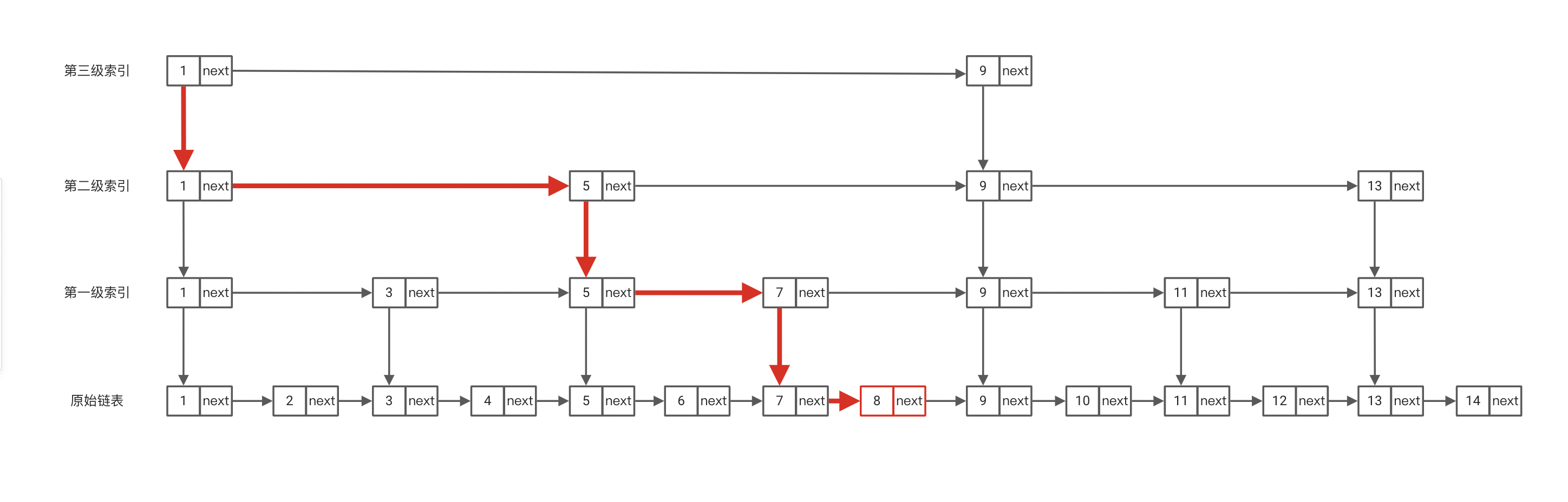
删除
在对跳表元素删除的时候需要注意的是要将对应的索引也进行删除
资料
源码:可查看 java.util.concurrent 下的 ConcurrentSkipListMap 或者redis的源码
论文:skiplists.pdf
相关博客:
https://leetcode-cn.com/problems/design-skiplist/
http://zhangtielei.com/posts/blog-redis-skiplist.html
https://cloud.tencent.com/developer/article/1353762