算法笔记-栈/堆/队列型

title: 算法笔记-栈/堆/队列型

index_img: ‘https://cdn.nlark.com/yuque/0/2022/png/2630542/1641449437813-e632e227-4fd4-44b2-81cf-d12d982cf959.png'

hide: false

password: ‘’

date: 2020-06-16 10:22:22

categories: [算法相关]

栈结构型

基于栈的先进后出特点，在处理某些问题上会更加方便

单调栈

  • 单调递增栈：单调递增栈就是从栈底到栈顶数据是从大到小
  • 单调递减栈：单调递减栈就是从栈底到栈顶数据是从小到大

队列

1
2
3
4
5
Queue<Integer> queue = new LinkedList<>()
//常用方法
queue.offer();//压入队列
queue.peek();//获取队头元素
queue.poll();//弹出队头
  • 优先队列
1
PriorityQueue queue = new PriorityQueue<>()

相关题目

有效的括号(简单)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    public boolean isValid(String s) {
        if (s.length() % 2 != 0) return false;
        Stack<Character> stack = new Stack<>();
        for (char c : s.toCharArray()) {
            if (c == '(' || c == '[' || c == '{') stack.push(c);
            else if (!stack.isEmpty()) {
                Character pop = stack.pop();
                if (check(pop, c)) continue;
                else {
                    stack.push(pop);
                    stack.push(c);
                }
            } else return false;
        }
        return stack.isEmpty();
    }

    //检查
    public boolean check(char a, char b) {
        if ((a == '{' && b == '}') || (a == '[' && b == ']') || (a == '(' && b == ')')) return true;
        return false;
    }
}

柱状图中最大的矩形(困难)

使用单调栈进行实现

单调栈 单调栈分为单调递增栈和单调递减栈

1
2
1. 单调递增栈即栈内元素保持单调递增的栈
2. 同理单调递减栈即栈内元素保持单调递减的栈

操作规则（下面都以单调递增栈为例）

1
2
1. 如果新的元素比栈顶元素大，就入栈
2. 如果新的元素较小，那就一直把栈内元素弹出来，直到栈顶比新元素小

加入这样一个规则之后，会有什么效果

1
2
1. 栈内的元素是递增的
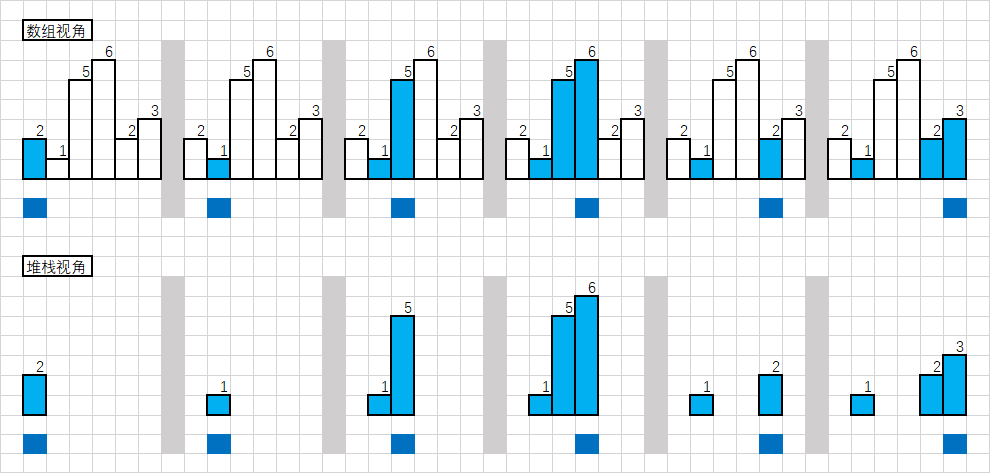
2. 当元素出栈时，说明这个新元素是出栈元素向后找第一个比其小的元素

举个例子，配合下图，现在索引在 6 ，栈里是 1 5 6 。 接下来新元素是 2 ，那么 6 需要出栈。 当 6 出栈时，右边 2 代表是 6 右边第一个比 6 小的元素。

当元素出栈后，说明新栈顶元素是出栈元素向前找第一个比其小的元素

当 6 出栈时，5 成为新的栈顶，那么 5 就是 6 左边第一个比 6 小的元素。

代码模板

1
2
3
4
5
6
7
8
9
stack<int> st;
for(int i = 0; i < nums.size(); i++)
{
	while(!st.empty() && st.top() > nums[i])
	{
		st.pop();
	}
	st.push(nums[i]);
}

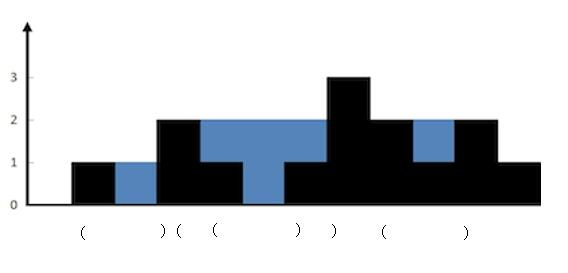
画图理解

思路

对于一个高度，如果能得到向左和向右的边界 那么就能对每个高度求一次面积 遍历所有高度，即可得出最大面积
使用单调栈，在出栈操作时得到前后边界并计算面积

答题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
int largestRectangleArea(vector<int>& heights)
{
    int ans = 0;
    vector<int> st;
    heights.insert(heights.begin(), 0);
    heights.push_back(0);
    for (int i = 0; i < heights.size(); i++)
    {
        while (!st.empty() && heights[st.back()] > heights[i])
        {
            int cur = st.back();
            st.pop_back();
            int left = st.back() + 1;
            int right = i - 1;
            ans = max(ans, (right - left + 1) * heights[cur]);
        }
        st.push_back(i);
    }
    return ans;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    public int largestRectangleArea(int[] heights) {
        int n = heights.length;
        int[] left = new int[n];
        int[] right = new int[n];
        Arrays.fill(right, n);

        Stack<Integer> mono_stack = new Stack<Integer>();
        for (int i = 0; i < n; ++i) {
            while (!mono_stack.isEmpty() && heights[mono_stack.peek()] >= heights[i]) {
                right[mono_stack.peek()] = i;
                mono_stack.pop();
            }
            left[i] = (mono_stack.isEmpty() ? -1 : mono_stack.peek());
            mono_stack.push(i);
        }

        int ans = 0;
        for (int i = 0; i < n; ++i) {
            ans = Math.max(ans, (right[i] - left[i] - 1) * heights[i]);
        }
        return ans;
    }
}

接雨水(困难)

暴力解法、优化、双指针、单调栈

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
    public int trap6(int[] height) {
        int sum = 0;
        Stack<Integer> stack = new Stack<>();
        int current = 0;
        while (current < height.length) {
            //如果栈不空并且当前指向的高度大于栈顶高度就一直循环
            while (!stack.empty() && height[current] > height[stack.peek()]) {
                int h = height[stack.peek()]; //取出要出栈的元素
                stack.pop(); //出栈
                if (stack.empty()) { // 栈空就出去
                    break;
                }
                int distance = current - stack.peek() - 1; //两堵墙之前的距离。
                int min = Math.min(height[stack.peek()], height[current]);
                sum = sum + distance * (min - h);
            }
            stack.push(current); //当前指向的墙入栈
            current++; //指针后移
        }
        return sum;
    }
}

接雨水 II(困难)

  • 该方块不为最外层的方块；
  • 该方块自身的高度比其上下左右四个相邻的方块接水后的高度都要低；

我们假设初始时矩阵的每个格子都接满了水，其高度均为maxHeight,其中maxHeight为矩阵中高度最高的格子。我们知道方块接水后的高度为water[i][j],他的求解公式，方块(i,j)的接水的高度为:
water[i][j]=max(heightMap[i],min(water[i−1][j],water[i+1][j],water[i][j−1],water[i][j+1]))
我们知道方块 (i,j)(i,j) 实际接水的容量计算公式为 water[i][j] - heightMap[i][j]
我们首先假设每个方块 (i,j) 的接水后的高度均为 water[i][j] = maxHeight，首先我们知道最外层的方块的肯定不能接水，所有的多余的水都会从最外层的方块溢出，我们每次发现当前方块 (i,j) 的接水高度 water[i][j] 小于与它相邻的 4 个模块的接水高度时，则我们将进行调整接水高度，我们将其相邻的四个方块的接水高度调整与 (i,j) 的高度保持一致，我们不断重复的进行调整，直到所有的方块的接水高度不再有调整时即为满足要求。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
class Solution {
    public int trapRainWater(int[][] heightMap) {
        int m = heightMap.length;
        int n = heightMap[0].length;
        //方向数组　把dx和dy压缩成一维来做
        int[] dirs = {-1, 0, 1, 0, -1};
        int maxHeight = 0;
        //找出最大值
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                maxHeight = Math.max(maxHeight, heightMap[i][j]);
            }
        }
        //全部设置为最大值
        int[][] water = new int[m][n];
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j){
                water[i][j] = maxHeight;      
            }
        }  
        //构建队列
        Queue<int[]> qu = new LinkedList<>();
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (i == 0 || i == m - 1 || j == 0 || j == n - 1) {//最外一圈
                    if (water[i][j] > heightMap[i][j]) {
                        water[i][j] = heightMap[i][j];
                        qu.offer(new int[]{i, j});
                    }
                }
            }
        } 
        //广度优先遍历
        while (!qu.isEmpty()) {
            int[] curr = qu.poll();
            int x = curr[0];
            int y = curr[1];
            //搜索四个方向
            for (int i = 0; i < 4; ++i) {
                //四周坐标
                int nx = x + dirs[i], ny = y + dirs[i + 1];
                //坐标越界
                if (nx < 0 || nx >= m || ny < 0 || ny >= n) {
                    continue;
                }
                //如果当前坐标水位 < 某一个方向水位　&& 某一个水位 > 矩阵中高度
                if (water[x][y] < water[nx][ny] && water[nx][ny] > heightMap[nx][ny]) {
                    //当前水位还可以进行装
                    water[nx][ny] = Math.max(water[x][y], heightMap[nx][ny]);
                    qu.offer(new int[]{nx, ny});
                }
            }
        }

        int res = 0;
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                res += water[i][j] - heightMap[i][j];
            }
        }
        return res;
    }
}

每日温度(中等)

暴力解法 + 单调栈

下一个更大元素 I (easy)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution {
    //stack and map
    //单调栈存储nums2的值，栈顶到栈底逐渐增大，当我们查找num1时，肯定是优先比较靠近的，因为栈递增，所以在构建栈的时候我们即可知道当前num的右边第一个大于他的数
    public int[] nextGreaterElement(int[] nums1, int[] nums2) {
        Map<Integer,Integer> map = new HashMap<>();
        Stack<Integer> stack = new Stack<>();
        //构建单调栈
        for(int i=nums2.length-1;i>=0;i--){
            int num = nums2[i];
            while(!stack.isEmpty()&#>=stack.peek())stack.pop();//栈顶元素小于num弹出
            map.put(num,stack.isEmpty()?-1:stack.peek());//记录元素num右边第一个大于num数的值
            stack.push(num);//压入当前num
        }
        for(int i=0;i<nums1.length;i++){
            nums1[i] = map.get(nums1[i]);
        }
        return nums1;
    }
    //bf
    public int[] nextGreaterElementByBF(int[] nums1, int[] nums2) {
        Map<Integer,Integer> map = new HashMap<>();
        for(int i=0;i<nums2.length;i++)map.put(nums2[i],i);
        for(int i=0;i<nums1.length;i++){
            int index = -1;
            for(int k=map.get(nums1[i]);k<nums2.length;k++){
                if(nums2[k]>nums1[i]){
                    index = nums2[k];
                    break;
                    }
                }
            nums1[i] = index;
        }
        return nums1;
    }
}

下一个更大元素 II

暴力解法、单调栈

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    //单调栈中保存的是下标，从栈底到栈顶的下标在数组 nums 中对应的值是单调不升的(顶小底大)。
    //每次我们移动到数组中的一个新的位置 i，我们就将当前单调栈中所有对应值小于 nums[i] 的下标弹出单调栈，这些值的下一个更大元素即为 nums[i]
    // （证明很简单：如果有更靠前的更大元素，那么这些位置将被提前弹出栈）。随后我们将位置 i 入栈。
    //但是注意到只遍历一次序列是不够的，例如序列 [2,3,1]，最后单调栈中将剩余 [3,1]，其中元素 [1] 的下一个更大元素还是不知道的。
    //一个朴素的思想是，我们可以把这个循环数组「拉直」，即复制该序列的前 n−1 个元素拼接在原序列的后面。这样我们就可以将这个新序列当作普通序列，用上文的方法来处理。
    //而在本题中，我们不需要显性地将该循环数组「拉直」，而只需要在处理时对下标取模即可。
    public int[] nextGreaterElements(int[] nums) {
        int n = nums.length;
        int[] ret = new int[n];
        Arrays.fill(ret, -1);
        Stack<Integer> stack = new Stack<Integer>();
        for (int i = 0; i < n * 2 - 1; i++) {
            while (!stack.isEmpty() && nums[stack.peek()] < nums[i % n]) {
                ret[stack.pop()] = nums[i % n];
            }
            stack.push(i % n);//存的是下标
        }
        return ret;
    }
}

下一个更大元素 III

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
public class Solution {
	//思路: 从右往左找到第一对连续的数字 a[i] 和 a[i−1] 满足 a[i−1]<a[i]。到当前位置，
    //a[i−1] 右边的数字没办法产生一个更大的排列，因为右边的数字是[降序]的。
    //所以我们需要重新排布 a[i−1] 到最右边的数字来得到下一个排列。
    
	//那么怎样排布能得到下一个更大的数字呢？
    //我们想得到恰好大于当前数字的下一个排列，所以我们需要用恰好大于 a[i−1] 的数字去替换掉 a[i−1]，比方说我们让这个数字为 a[j]。
	//我们将 a[i−1] 和 a[j] 交换，我们现在在下标为 i−1 的地方得到了正确的数字，但当前的结果还不是一个正确的排列。
    //我们需要用从 i−1 开始到最右边数字剩下来的数字升序排列，来得到它们中的最小排列。
	//我们注意到在从右往左找到第一对 a[i−1]<a[i] 的连续数字前， a[i−1] 右边的数字都是降序排列的，
    //所以交换 a[i−1] 和 a[j] 不会改变下标从 i 开始到最后的顺序。所以我们在交换了 a[i−1] 和 a[j] 以后，
    //只需要反转下标从 i 开始到最后的数字，就可以得到下一个字典序最小的排列。
    //
    //例如
    //158476531
    //1.从右向左查找a[i−1]<a[i]即a[3]<a[4],i=4,即[476531]
    //2.从右向左查找第一个比a[i−1]大的数与它进行交换，即[576431]
    //3.翻转[76431]得[13467]
    //答案即158'5''13467'
    public int nextGreaterElement(int n) {
        char[] a = ("" + n).toCharArray();//转为数组进行操作
        int i = a.length - 2;//初始化i长度
        //查找第一对a[i-1]<a[i]的位置
        while (i >= 0 && a[i + 1] <= a[i]) i--;
        if (i < 0) return -1;//不存在直接返回-1
        int j = a.length - 1;
        //查找比a[i-1]大的数
        while (j >= 0 && a[j] <= a[i]) j--;
        //交换i和j的值
        swap(a, i, j);
        //翻转i+1-n的数
        reverse(a, i + 1);
        //转为整数
        try {
            return Integer.parseInt(new String(a));
        } catch (Exception e) {
            return -1;
        }
    }
    private void reverse(char[] a, int start) {
        int i = start, j = a.length - 1;
        while (i < j) {
            swap(a, i, j);
            i++;
            j--;
        }
    }
    private void swap(char[] a, int i, int j) {
        char temp = a[i];
        a[i] = a[j];
        a[j] = temp;
    }
}

去除重复字母(困难)

栈 + 哨兵技巧（Java、C++、Python）

股票价格跨度(中等)

单调栈

最短无序连续子数组()

1

简化路径（中等）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
//思路：使用‘/’进行分割得到的结果类型有
//1.空字符串。例如当出现多个连续的 /，就会分割出空字符串
//2.一个点 .
//3.两个点 ..
//4.只包含英文字母、数字或下划线的目录名。
//
//当遇到「空字符串」以及「一个点」，无需对它们进行处理
class Solution {
    public String simplifyPath(String path) {
        String[] names = path.split("/");
        Deque<String> stack = new ArrayDeque<String>();
        for (String name : names) {
            if ("..".equals(name)) {//遇到'..'则弹栈，否则不是「空字符串」以及「一个点」压栈
                if (!stack.isEmpty()) {
                    stack.pollLast();
                }
            } else if (name.length() > 0 && !".".equals(name)) {
                stack.offerLast(name);
            }
        }
        //拼接处理
        StringBuffer ans = new StringBuffer();
        if (stack.isEmpty()) {
            ans.append('/');
        } else {
            while (!stack.isEmpty()) {
                ans.append('/');
                ans.append(stack.pollFirst());
            }
        }
        return ans.toString();
    }
}

括号的最大嵌套深度（easy）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
	//遇到左括号++且比较size，右括号--
    public int maxDepth(String s) {
        int ans = 0, size = 0;
        for (int i = 0; i < s.length(); ++i) {
            char ch = s.charAt(i);
            if (ch == '(') {
                ++size;
                ans = Math.max(ans, size);
            } else if (ch == ')') {
                --size;
            }
        }
        return ans;
    }
}

用栈实现队列（easy）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
//使用两个栈（输入栈，输出栈），当输出栈为空则将输入栈弹进输出栈
class MyQueue {
    Stack<Integer> stackA;
    Stack<Integer> stackB;
    public MyQueue() {
        stackA = new Stack<Integer>();
        stackB = new Stack<Integer>();
    }
    public void push(int x) {
        stackA.push(x);
    }
    public int pop() {
        if(stackB.isEmpty())
        while(!this.stackA.isEmpty()){
            Integer pop = stackA.pop();
            stackB.push(pop);
        }
        return stackB.pop();
    }
    public int peek() {
        if(stackB.isEmpty())
        while(!this.stackA.isEmpty()){
            Integer pop = stackA.pop();
            stackB.push(pop);
        }
        return stackB.peek();
    }
    public boolean empty() {
        return this.stackA.isEmpty()&&this.stackB.isEmpty();
    }
}

用队列实现栈（easy）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
//两个队列实现
class MyStack {
    //思路：一个队列存储值，另一个队列作为入栈的辅助队列。进栈先入queueB，在将queueB元素移过来（此时新元素即是队首），交换queueA和QueueB
    LinkedList<Integer> queueA;
    LinkedList<Integer> queueB;
    public MyStack() {
        queueA = new LinkedList();
        queueB = new LinkedList();
    }
    public void push(int x) {
        queueB.push(x);
        while(!queueA.isEmpty())queueB.offer(queueA.pop());
        LinkedList qa = queueA;
        queueA = queueB;
        queueB = qa;
    }
    public int pop() {
        return queueA.pop();
    }
    
    public int top() {
        return queueA.peek();
    }
    
    public boolean empty() {
        return queueA.isEmpty();
    }
}
//一个队列实现
class MyStack {
		//思路: 通过每次将队列的值旋转到末尾
    Queue<Integer> queue;
    public MyStack() {
        queue = new LinkedList<Integer>();
    }
    public void push(int x) {
        int n = queue.size();
        queue.offer(x);
        for (int i = 0; i < n; i++) {
            queue.offer(queue.poll());
        }
    }
    public int pop() {
        return queue.poll();
    }
    public int top() {
        return queue.peek();
    }
    public boolean empty() {
        return queue.isEmpty();
    }
}

最小栈（easy）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class MinStack {
    //一个正在栈，一个单调栈（个数一样）
    Deque<Integer> xStack;
    Deque<Integer> minStack;
    public MinStack() {
        xStack = new LinkedList<Integer>();
        minStack = new LinkedList<Integer>();
        minStack.push(Integer.MAX_VALUE);
    }
    public void push(int x) {
        xStack.push(x);
        minStack.push(Math.min(minStack.peek(), x));
    }
    public void pop() {
        xStack.pop();
        minStack.pop();
    }
    public int top() {
        return xStack.peek();
    }
    public int getMin() {
        return minStack.peek();
    }
}

字符串解码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
class Solution {
    //思路:借助栈
    public String decodeString(String s) {
        StringBuilder sb = new StringBuilder();
        Stack<String> stack = new Stack<>();
        for(int i=0;i<s.length();i++){
            char c = s.charAt(i);
            if(c=='['){//压栈
                int start = i, end = i;
                //遇到字母和]停止
                while(start>0&&s.charAt(start-1)>='0'&&s.charAt(start-1)<='9')start--;
                while(end+1<s.length()&&s.charAt(end+1)>='a'&&s.charAt(end+1)<='z')end++;
                String str = s.substring(start,end+1);
                stack.push(str);
                i=end;
            }else if(c==']'){//弹栈
                String p = stack.pop();
                int idx = p.indexOf('[');
                int size = 0;
                for(int j=0;j<idx;j++)size=size*10+p.charAt(j)-'0';
                String str = p.substring(idx+1,p.length());
                StringBuilder sbr = new StringBuilder();
                for(int j=0;j<size;j++)sbr.append(str);
                if(!stack.isEmpty()){
                    String pop = stack.pop();
                    pop+=sbr.toString();
                    stack.push(pop);
                }else sb.append(sbr.toString());
            }else if(c>='A'&&c<='z'){
                if(!stack.isEmpty()){
                    String pop = stack.pop();
                    pop+=c;
                    stack.push(pop);
                }else sb.append(c);
            }
        }
        return sb.toString();
    }
}
//递归
class Solution {
    String src;
    int ptr;
    public String decodeString(String s) {
        src = s;
        ptr = 0;
        return getString();
    }
    public String getString() {
        if (ptr == src.length() || src.charAt(ptr) == ']') {
            // String -> EPS
            return "";
        }
        char cur = src.charAt(ptr);
        int repTime = 1;
        String ret = "";
        if (Character.isDigit(cur)) {
            // String -> Digits [ String ] String
            // 解析 Digits
            repTime = getDigits(); 
            // 过滤左括号
            ++ptr;
            // 解析 String
            String str = getString(); 
            // 过滤右括号
            ++ptr;
            // 构造字符串
            while (repTime-- > 0) {
                ret += str;
            }
        } else if (Character.isLetter(cur)) {
            // String -> Char String
            // 解析 Char
            ret = String.valueOf(src.charAt(ptr++));
        }
        return ret + getString();
    }
    public int getDigits() {
        int ret = 0;
        while (ptr < src.length() && Character.isDigit(src.charAt(ptr))) {
            ret = ret * 10 + src.charAt(ptr++) - '0';
        }
        return ret;
    }
}

基本计算器

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution {
    //思路：栈+符号位
    //表达式只有加和减，其实开括号影响的是括号前面的数，如果是正数不变，负数括号内的符号取反
    public int calculate(String s) {
        Stack<Integer> stack = new Stack<>();
        stack.push(1);
        int i=0;
        int ans=0;
        int sign = 1;
        while(i<s.length()){
            char c = s.charAt(i);
            if(c==' ')i++;
            else if(c=='+'){//
                sign = stack.peek();
                i++;
            }else if(c=='-'){//更新sign
                sign = -stack.peek();
                i++;
            }else if(c=='('){
                stack.push(sign);
                i++;
            }else if(c==')'){
                stack.pop();
                i++;
            }else{
                long num = 0;
                while(i<s.length()&&Character.isDigit(s.charAt(i))){
                    num = num * 10 + s.charAt(i)-'0';
                    i++;
                }
                ans+=sign*num;
            }
        }
        return ans;
    }
}

基本计算器 II

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
class Solution {
		//思路：栈来保存每一项，遇到*和/先与栈顶运算在压，最后全部弹栈求和
    public int calculate(String s) {
        // 保存上一个符号，初始为 +
        char sign = '+';
        Stack<Integer> numStack = new Stack<>();
        // 保存当前数字，如：12是两个字符，需要进位累加
        int num = 0;
        int result = 0;
        for(int i = 0; i < s.length(); i++){
            char cur = s.charAt(i);
            if(cur >= '0'){
                // 记录当前数字。先减，防溢出
                num = num*10 - '0' + cur;
            }
            if((cur < '0' && cur !=' ' )|| i == s.length()-1){
                // 判断上一个符号是什么
                switch(sign){
                    // 当前符号前的数字直接压栈
                    case '+': numStack.push(num);break;
                    // 当前符号前的数字取反压栈
                    case '-': numStack.push(-num);break;
                    // 数字栈栈顶数字出栈，与当前符号前的数字相乘，结果值压栈
                    case '*': numStack.push(numStack.pop()*num);break;
                    // 数字栈栈顶数字出栈，除于当前符号前的数字，结果值压栈
                    case '/': numStack.push(numStack.pop()/num);break;
                }
                // 记录当前符号
                sign = cur;
                // 数字清零
                num = 0;
            }
        }
        // 将栈内剩余数字累加，即为结果
        while(!numStack.isEmpty()){
            result += numStack.pop();
        }
        return result;
    }
}

移掉 K 位数字

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
思路：
1.给定一个长度为n的数字序列D[0,1,2,3,4...,n-1]，从左往右找到第一个位置（i>0）使得 D[i]<D[i−1]，并删去 D[i−1]；如果不存在，说明整个数字序列单调不降，删去最后一个数字即可,可以继续使用同样的策略，直至删除 k 次。
2.基于1可知其时间复杂度为O(nk),我们可以加速其维护一个单调递增的栈：当遇到单调递增的进栈，当遇到比当天栈顶小的，弹栈直到
  2.1 栈为空
  2.2 或者新的栈顶元素不大于当前数字
  2.3 或者我们已经删除了 kk 位数字
public String removeKdigits(String num, int k) {
        Stack<Character> stack = new Stack<>();
        int n = num.length();
        if(n==k)return "0";
        for(int i=0;i<n;i++){
            char c = num.charAt(i);
            while(!stack.isEmpty()&&k>0&&stack.peek()>c){
                stack.pop();
                k--;
            }
            stack.push(c);
        }
        for (int i = 0; i < k; ++i) {
            stack.pop();
        }
        StringBuilder sb = new StringBuilder();
        while(!stack.isEmpty()){
            sb.append(stack.pop());
        }
        sb.reverse();
        int l = sb.length();
        if(sb.charAt(0)=='0'&&l>1)
        for(int i=0;i<l;i++){
            if(sb.charAt(0)!='0'||sb.length()==1)break;
            sb.deleteCharAt(0);
        }
        return sb.toString();
    }

有效的括号字符串

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
class Solution {
		//1.栈实现：通过两个栈分别存储'('和'*'的下标，如果遇到')'则优先选择弹出'(',再考虑弹'*',最后判断'('栈剩余的元素是否能被'*'栈都抵消（'*'的下标必须都在'('之后才可以抵消)
		public boolean checkValidString(String s) {
        Stack<Integer> leftStack = new Stack<>();
        Stack<Integer> asteriskStack = new Stack<>();
        int n = s.length();
        for(int i=0;i<n;i++){
            char c = s.charAt(i);
            if(c=='(')leftStack.push(i);
            else if(c=='*')asteriskStack.push(i);
            else {
                if(!leftStack.isEmpty())leftStack.pop();
                else if(!asteriskStack.isEmpty())asteriskStack.pop();
                else return false;
            }
        }
        while(!leftStack.isEmpty()&&!asteriskStack.isEmpty()){
            Integer ai = asteriskStack.pop();
            Integer li = leftStack.pop();
            if(li>ai)return false;
        }
        return leftStack.isEmpty();
    }
    //2.动态规划
    //dp[i][j]表示前 i 个字符（字符下标从 1 开始），能否与 j 个右括号形成合法括号序列。
    //起始时只有 dp[0][0] 为 true，最终答案为 dp[n][0]。
    //dp[i][j] 有以下几种情况
    //1.当前字符为'(': dp[i][j] = dp[i-1][j-1]
    //2.当前字符为')': dp[i][j] = dp[i-1][j+1]
    //3.当前字符为'*': dp[i][j] = dp[i-1][j-1] V dp[i-1][j+1] V dp[i-1][j]
    public boolean checkValidString(String s) {
        int n = s.length();
        boolean[][] f = new boolean[n + 1][n + 1];
        f[0][0] = true;
        for (int i = 1; i <= n; i++) {
            char c = s.charAt(i - 1);
            for (int j = 0; j <= i; j++) {
                if (c == '(') {
                    if (j - 1 >= 0) f[i][j] = f[i - 1][j - 1];
                } else if (c == ')') {
                    if (j + 1 <= i) f[i][j] = f[i - 1][j + 1];
                } else {
                    f[i][j] = f[i - 1][j];
                    if (j - 1 >= 0) f[i][j] |= f[i - 1][j - 1];
                    if (j + 1 <= i) f[i][j] |= f[i - 1][j + 1];
                }
            }
        }
        return f[n][0];
    }
    //3.模拟
    public boolean checkValidString(String s) {
        // l: 左括号最少可能有多少个
        // r: 左括号最多可能有多少个
        int l = 0, r = 0;
        for (char c : s.toCharArray()) {
            // 遇到'('所有可能性加一
            // 遇到')'所有可能性减一
            // 遇到'*'，最少的可能性可以变少，最多的可能性也同样可以变多，这取决于这个星号最终我们看成什么，但是可能性都在
            if (c == '(') {
                l++; r++;
            } else if (c == ')') {
                l--; r--;
            } else {
                l--; r++;
            }
            // 当前左括号最少个数不能为负
            l = Math.max(l, 0);
            // 这种情况其实发生在r本身是负数的时候，也就是我们常见的右括号太多了
            if (l > r) return false;
        }
        // 能取到0个左括号才是满足平衡的
        return l == 0;
    }
}

数据流的中位数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class MedianFinder {
    //思路：两个堆，最大堆和最小堆。最大堆存小于中位数的数，最小于堆存大于中位数的数，保证大堆顶元素个数比小堆顶最多只能大1
    private PriorityQueue<Integer> minQue;//8,9,10,11,12,13,14
    private PriorityQueue<Integer> maxQue;//1,2,3,4,5,6,7
    public MedianFinder() {
        minQue = new PriorityQueue<>();//默认小堆顶
        maxQue = new PriorityQueue<>((a,b)->(b-a));//大堆顶
    }
    public void addNum(int num) {
        if(maxQue.isEmpty()||num<=maxQue.peek()){
            maxQue.offer(num);
            if(minQue.size()+1<maxQue.size())//保证大堆顶元素个数比小堆顶最多只能大1
            minQue.offer(maxQue.poll());
        }else{
            minQue.offer(num);
            if(minQue.size()>maxQue.size())//保证大堆顶元素个数比小堆顶最多只能大1
            maxQue.offer(minQue.poll());
        }
    }
    public double findMedian() {
        if(maxQue.size()>minQue.size())return maxQue.peek();//此时大堆顶的堆顶为中位数
        return (minQue.peek()+maxQue.peek())/2.0;//取两个堆队首
    }
}

218. 天际线问题（hard)

https://leetcode-cn.com/problems/the-skyline-problem/solution/gong-shui-san-xie-sao-miao-xian-suan-fa-0z6xc/

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
class Solution {
    //思路：将相邻的建筑物看作一个整体，可以理解为求相邻两个矩阵最上边的左端点。因此我们需要实时维护一个最大高度，可以使用优先队列（堆）
    //1.按照left排序同事构造可以区分左右端点的列表。
    //2.通过堆存储遍历过的高度，如果是左端点且与前一个高度不一致则记录
    public List<List<Integer>> getSkyline(int[][] bs) {
        List<List<Integer>> ret = new ArrayList<>();
        // 预处理所有的点，为了方便排序，对于左端点，令高度为负；对于右端点令高度为正
        List<int[]> ps = new ArrayList<>();
        for (int[] b : bs) {
            int l = b[0], r = b[1], h = b[2];
            ps.add(new int[]{l, -h});
            ps.add(new int[]{r, h});
        }
        // 先按照横坐标进行排序
        // 如果横坐标相同，则按照左端点排序
        // 如果相同的左/右端点，则按照高度进行排序
        Collections.sort(ps, (a, b)->a[0] != b[0] ? a[0] - b[0]:a[1] - b[1]);
        // 大根堆存储高度
        PriorityQueue<Integer> queue = new PriorityQueue<>((a,b)->b-a);
        int prev = 0;
        queue.add(prev);
        //遍历排序后的点
        for (int[] p : ps) {
            int point = p[0], height = p[1];
            if (height < 0) {
                // 如果是左端点，说明存在一条往右延伸的可记录的边，将高度存入优先队列
                queue.add(-height);
            } else {
                // 如果是右端点，说明这条边结束了，将当前高度从队列中移除
                queue.remove(height);
            }
            // 取出最高高度，如果当前不与前一矩形“上边”延展而来的那些边重合，则可以被记录
            int cur = queue.peek();
            if (cur != prev) {
                List<Integer> list = new ArrayList<>();
                list.add(point);
                list.add(cur);
                ret.add(list);
                prev = cur;
            }
        }
        return ret;
    }
}

面试题 17.14. 最小K个数（mid)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public int[] smallestK(int[] arr, int k) {
        int[] ret = new int[k];
        if(k==0)return ret;
        //大堆顶
        PriorityQueue<Integer> queue = new PriorityQueue<>((o1,o2)->o2-o1); 
        for(int num:arr){
            if(queue.size()<k){
                queue.offer(num);
            }else if(queue.size()==k&&queue.peek()>num){
                queue.poll();
                queue.offer(num);
            }
        }
        while(!queue.isEmpty())ret[--k]=queue.poll();
        return ret;
    }
}

1606. 找到处理最多请求的服务器（hard）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
    public List<Integer> busiestServers(int k, int[] arrival, int[] load) {
        //k台服务器
        int[] freq = new int[k];//0表示空闲,1表示正在使用
        TreeSet<Integer> treeSet = new TreeSet<>();
        List<Integer> ret = new ArrayList<>();
        //小堆顶存储结束时间
        PriorityQueue<int[]> queue = new PriorityQueue<>(Comparator.comparingInt(x -> x[1]));
        int n = arrival.length;
        for (int i = 0; i < k; i++) {
            treeSet.add(i);
        }
        for (int i = 0; i < n; i++) {
            while (!queue.isEmpty() && queue.peek()[1] <= arrival[i]) {
                treeSet.add(queue.poll()[0]);
            }
            //无剩余服务器
            if (treeSet.isEmpty()) continue;
            //获取剩余的可用的服务器（超时）
            // 如何能获取最靠近i的空闲机器?TreeMap
            Integer ceiling = treeSet.ceiling(i % k);
            if (ceiling==null)ceiling = treeSet.first();
            //压入堆
            queue.offer(new int[]{ceiling, arrival[i] + load[i]});
            //记录服务器处理次数
            treeSet.remove(ceiling);
            freq[ceiling]++;
        }
        int maxIndex = 0;
        for (int i = 1; i < k; i++)  maxIndex = freq[i] > freq[maxIndex] ? i : maxIndex;
        for (int i = 0; i < k; i++) if (freq[i] == freq[maxIndex]) ret.add(i);
        return ret;
    }
}

220. 存在重复元素 III（mid)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
class Solution {
    //1.bf超时
    //2.基于条件分析:
    //abs(nums[i] - nums[j]) <= t
    //abs(i - j) <= k
    //可知我们需要控制两个地方,一个是nums的值、另一个是下标
    //BF最耗时的地方,每次都要从[i-k,i][i,i+k],开始查找并判断大小,因为取的是绝对值nums[i] - nums[j]和nums[j] - nums[i]一样(i和j同理),所以只需要维护一个方向
    //所以使用大小为k的有序集合TreeSet能有效解决这个问题
    //维护一个大小为k的TreeSet存储nums[i]的值,大小为k是为了控制下标,值有序我们可以快速的取出比当前大的值(不像BF需要一个一个比较)
    //遍历nums计算出当前nums[j]的可取范围,在TreeSet中ceiling出(nums[i]-t),就是在TreeSet查找比nums[i]-t大的数,
    //如果有比nums[i]-t大的,且小于nums[i]+t直接返回true,在遍历的同时维护TreeSet大小为k
    //nums[j]取值范围：上限nums[i]+t,下限nums[i]-t,
    //
    //1.为什么nums[j]上限是nums[i]+t,下限是nums[i]-t,通过解开绝对值就可得出.
    public boolean containsNearbyAlmostDuplicate(int[] nums, int k, int t) {
        int n = nums.length;
        TreeSet<Long> set = new TreeSet<Long>();
        for (int i = 0; i < n; i++) {
            //查找比nums[i]-t大的数
            Long ceiling = set.ceiling((long) nums[i] - (long) t);
            //如果有比nums[i]-t大的,且小于nums[i]+t直接返回true
            if (ceiling != null && ceiling <= (long) nums[i] + (long) t) {
                return true;
            }
            //添加进集合
            set.add((long) nums[i]);
            if (i >= k) {//维护大小为k的有序集合
                set.remove((long) nums[i - k]);
            }
        }
        return false;
    }
    public boolean containsNearbyAlmostDuplicateBF(int[] nums, int k, int t) {
        int n  =nums.length;
        for(int i=0;i<n;i++){
            for(int j=i+1;j<n;j++){
                if(Math.abs(i-j)>k)continue;
                if(Math.abs(((long)nums[i] - (long)nums[j]))<=t)return true;
            }
        }
        return false;
    }
}

相关资料

基础算法 > 刷题记录
算法笔记-栈/堆/队列型
https://mikeygithub.github.io/2021/12/29/yuque/算法笔记-栈!堆!队列型/
作者
Mikey
发布于
2021年12月29日
许可协议