算法笔记-二叉树/线段树/排序树

title: 算法笔记-二叉树/线段树/排序树

index_img: ‘https://cdn.nlark.com/yuque/0/2023/png/2630542/1673112982757-5ae72879-a909-4654-a75e-8c64152f29ca.png'

hide: false

password: ‘’

date: 2019-10-10 17:24:22

categories: [算法相关]

必备知识

遍历方式

在树的题目当中主要围绕着,前序、中序、后续、广度、深度遍历来进行解题，所以掌握其十分重要，直接上迭代版本，递归太简单就不上了

前序遍历-通过栈实现

(先压入右结点)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
  public List<Integer> preorderTraversal(TreeNode root) {
      if (root == null) {
          return new ArrayList<>();
      } else {
          List<Integer> list = new ArrayList<>();
          Stack<TreeNode> stack = new Stack<>();
          stack.push(root);
          while (!stack.isEmpty()) {
              TreeNode tmp = stack.pop();
              list.add(tmp.val);
              if (tmp.right != null)
                  stack.push(tmp.right);
              if (tmp.left != null)
                  stack.push(tmp.left);
          }
          return list;
      }
  }
}

中序遍历-通过栈实现

(一路向左把沿途结点压入栈)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
  public List<Integer> inorderTraversal(TreeNode root) {
      if (root == null) {
          return new ArrayList<>();
      } else {
          Stack<TreeNode> stack = new Stack<>();
          List<Integer> list = new ArrayList<>();
          while (root != null || !stack.isEmpty()) {
              while (root != null) {// 一路向左把沿途结点压入栈
                  stack.push(root);
                  root = root.left;
              }
              if (!stack.isEmpty()) {
                  root = stack.pop();// 弹出栈
                  list.add(root.val);
                  root = root.right;// 转向右节点
              }
          }
          return list;
      }
  }
}

后序遍历-通过栈实现

(前序先push-left再reverse)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
  public List<Integer> postorderTreversal(TreeNode root) {
      if (root == null) {
          return new ArrayList<>();
      } else {
          List<Integer> list = new ArrayList<>();
          Stack<TreeNode> stack = new Stack<>();
          stack.push(root);
          while (!stack.isEmpty()) {
              TreeNode tmp = stack.pop();
              list.add(tmp.val);
              if (tmp.left != null) {
                  stack.push(tmp.left);
              }
              if (tmp.right != null) {
                  stack.push(tmp.right);
              }
          }
          Collections.reverse(list);
          return list;
      }
  }
}

广度优先-通过队列实现

借助队列

1
2
3
4
5
6
7
8
9
10
11
class Solution {
    public void BFS(TreeNode root) {
        Queue<TreeNode> queue = new LinkedList<>();
        if (!Objects.isNull(root)) queue.add(root);
        while (!queue.isEmpty()) {
            TreeNode node = queue.poll();//出队
            if (node.left != null) queue.add(node.left);
            if (node.right != null) queue.add(node.right);
        }
    }
}

深度优先-通过栈实现

借助栈

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
    public List<Integer> DFS(TreeNode root) {
        List<Integer> list = new ArrayList<>();
        Stack<TreeNode> stack = new Stack<>();
        stack.push(root);
        while (!stack.isEmpty()) {
            TreeNode tmp = stack.pop();
            list.add(tmp.val);
            if (tmp.left != null) stack.push(tmp.left);
            if (tmp.right != null) stack.push(tmp.right);
        }
        return list;
    }
}

数类型

线段树

是一种非常灵活的数据结构，它可以用于解决多种范围查询问题，比如在对数时间内从数组中找到最小值、最大值、总和、最大公约数、最小公倍数等。

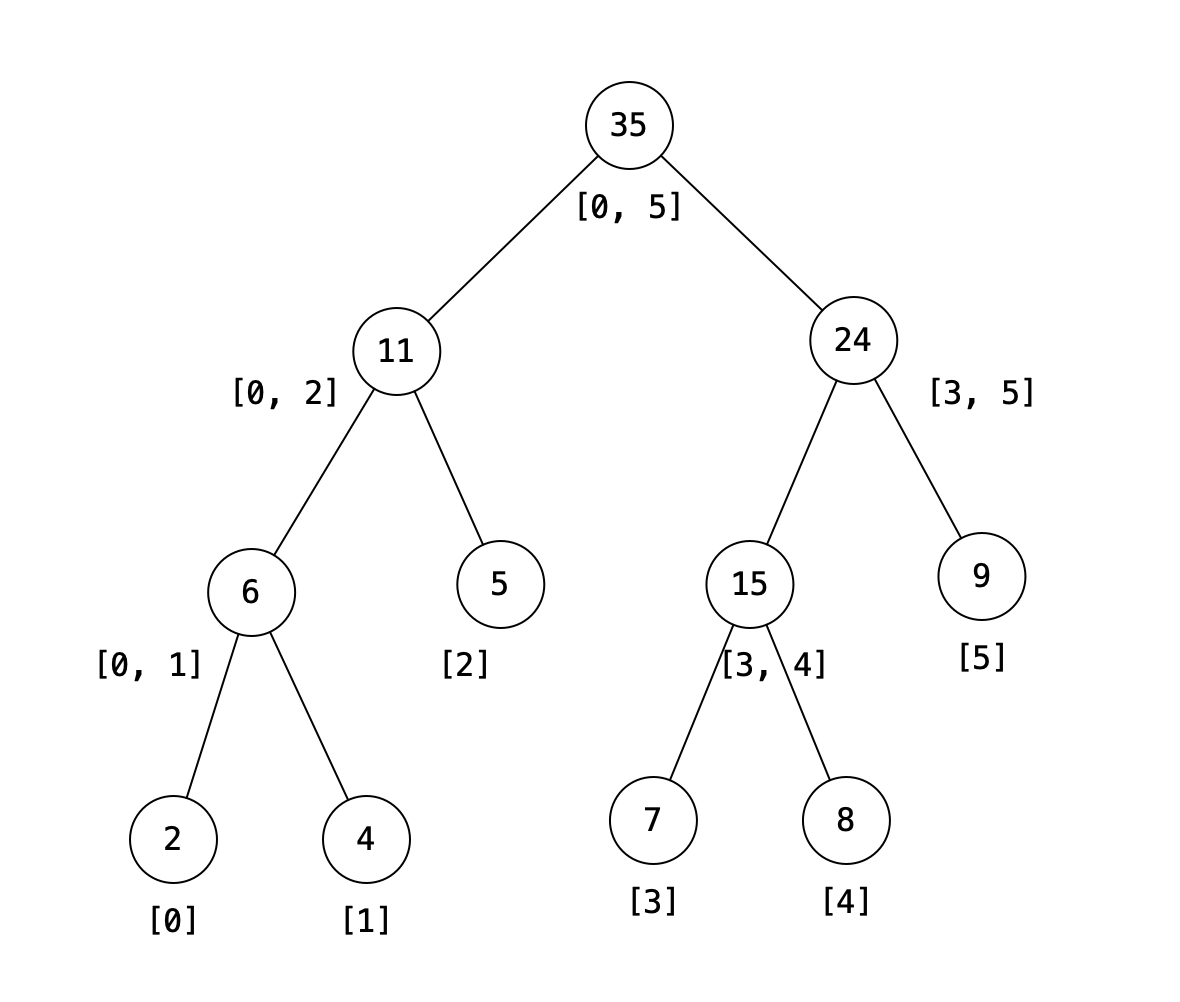
数组 A[0,1,…,n−1] 的线段树是一个二叉树，其中每个节点都包含数组的一个子范围 [i…j] 上的聚合信息（最小值、最大值、总和等），其左、右子节点分别包含范围 上的信息。

线段树既可以用数组也可以用树来实现。对于数组实现，如果索引 i 处的元素不是一个叶节点，那么其左子节点和右子节点分别存储在索引为 2i 和 2i+1 的元素处。

在上图所给出的示例中，每个叶节点都包含初始的数组元素 {2,4,5,7,8,9}。内部节点包含范围内相应元素的总和 - (11) 是从索引 0 到索引 2 的元素之和。而根节点 (35) 是它的两个子节点 (6) 和 (29) 的和,也是整个数组的和。

线段树可以分为以下三个步骤：

1.从给定数组构建线段树的预处理步骤。

2.修改元素时更新线段树。

3.使用线段树进行区域和检索。

相关题目

平衡二叉树(简单)

判断是否是平衡二叉树

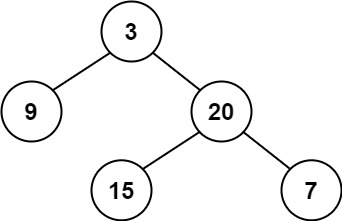
判断树是否为平衡二叉树

测试用例

输入：root = [3,9,20,null,null,15,7]
输出：true

解题思路

平衡二叉树：左右子树高度差不超过一，根据这一特点，递归判断各个节点的子树是否符合条件，不满足则直接返回false,直到递归完成。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
    /**
     * 判断是否为平衡二叉树(自顶向下O(n^2))
     * @param root
     * @return
     */
    public boolean isBalanced(TreeNode root) {
        if (root == null) return true;
        else return Math.abs(height(root.left) - height(root.right)) <= 1 && isBalanced(root.left) && isBalanced(root.right);
    }
    /**
     * 获取当前节点树高度
     * @param root
     * @return
     */
    public int height(TreeNode root) {
        if (root == null)  return 0;
        else return Math.max(height(root.left), height(root.right)) + 1;
    }
    //自底向上
    public boolean isBalanced(TreeNode root) {
        return depth(root)>=0;
    }
    public int depth(TreeNode root){
        if(root==null)return 0;
        int left = depth(root.left);
        int right = depth(root.right);
        if(left==-1||right==-1||Math.abs(left-right)>1)return -1;
        else return Math.max(left,right)+1;
    }
}

特定深度节点链表(中等)

特定深度节点链表

题目描述

给定一棵二叉树，设计一个算法，创建含有某一深度上所有节点的链表（比如，若一棵树的深度为 D，则会创建出 D 个链表）。返回一个包含所有深度的链表的数组。

示例

输入：[1,2,3,4,5,null,7,8]

1
2
3
4
5
    1
   /  \ 
  2    3
 / \    \ 
4   5    7

/ 8

输出：[[1],[2,3],[4,5,7],[8]]

实现思路

通过广度优先遍历对树进行逐层遍历构造链表，通过每一次获取当前队列长度读取当前层的元素个数(关键)

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {

    public static ListNode[] listOfDepth(TreeNode tree) {

        List<ListNode> listNodes = new ArrayList<>();
        //广度优先遍历
        Queue<TreeNode> queue = new LinkedList<>();
        queue.add(tree);
        while (!queue.isEmpty()) {
            int size = queue.size();//队列大小（核心）
            ListNode head, tmp;
            head = tmp = new ListNode(0);//链表临时头节点
            for (int i = 0; i < size; i++) {//循环当前层元素
                TreeNode treeNode = queue.poll();//从对头取当前元素
                //构建链表
                tmp.next = new ListNode(treeNode.val);
                tmp = tmp.next;
                //将下一层元素压入队列
                if (treeNode.left != null) queue.add(treeNode.left);
                if (treeNode.right != null) queue.add(treeNode.right);
            }
            //将每一条链表添加到list中
            listNodes.add(head.next);
        }

        return listNodes.toArray(new ListNode[]{});
    }
}

N叉树的前序遍历(简单)

N叉树的前序遍历

题目描述

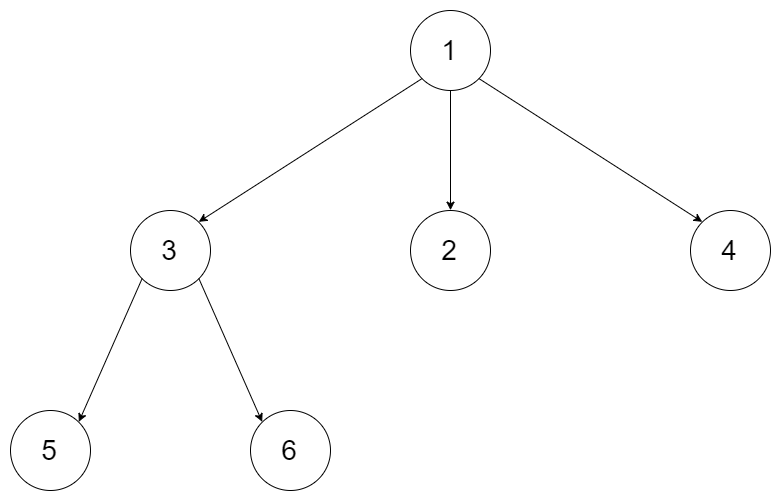
给定一个 N 叉树，返回其节点值的前序遍历。

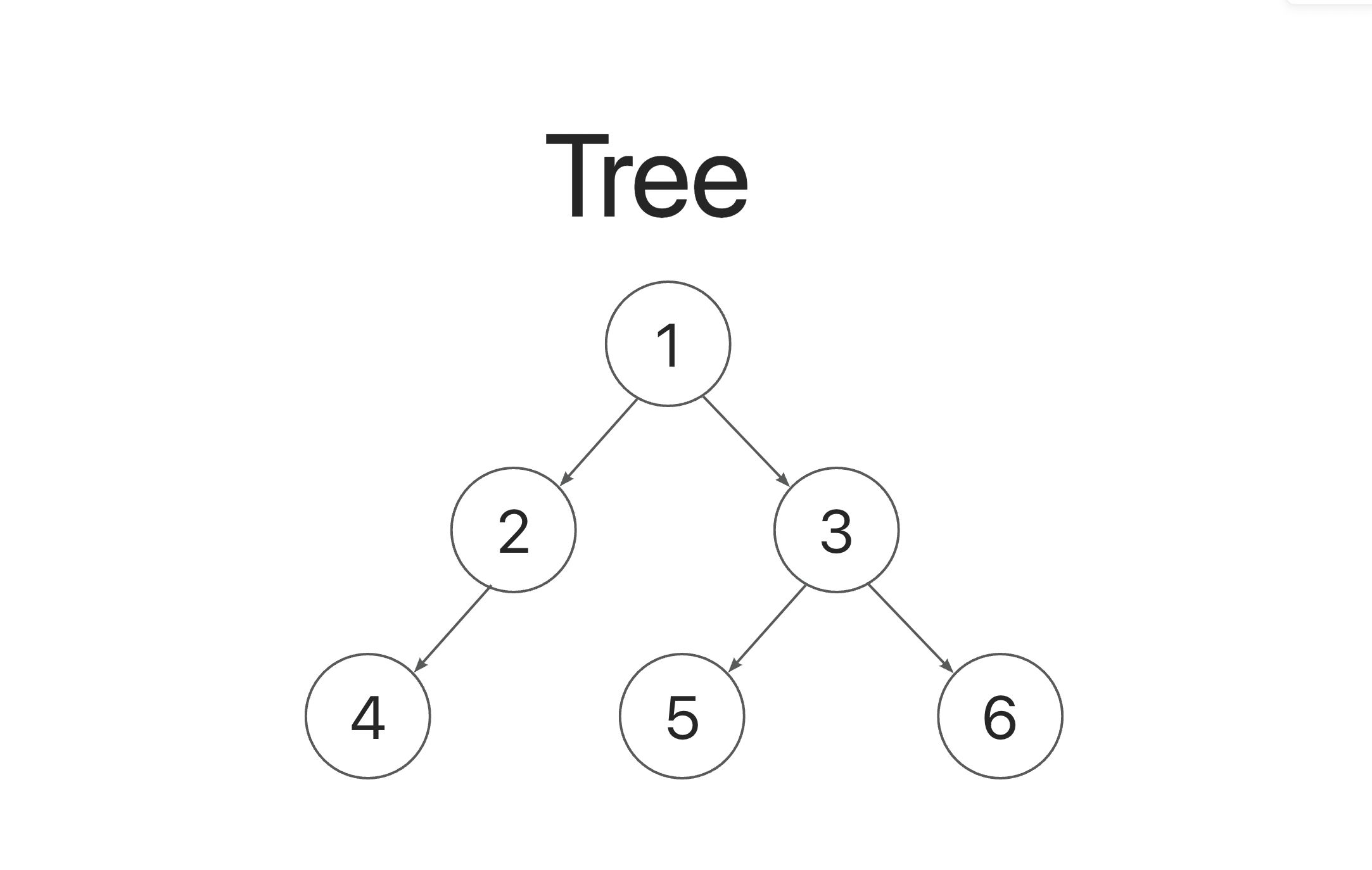
例如，给定一个 3叉树 :

返回其前序遍历: [1,3,5,6,2,4]。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
public class Tree {
   List<Integer> list = new ArrayList<>();

   public List<Integer> preorder(Node root) {
       list.add(root.val);
       //遍历子节点
       root.children.forEach(v -> {
           preorder(v);
       });
       return list;
   }

   public List<Integer> preorder(Node root) {
       //容器
       List<Integer> list = new ArrayList<>();
       Stack<Node> stack = new Stack<>();
       if (root == null) {
           return list;
       }
       //首个节点
       stack.push(root);
       //迭代
       while (!stack.empty()) {
           Node tmp = stack.pop();//出栈
           list.add(tmp.val);//插入值
           Collections.reverse(tmp.children);//将子节点进行反转
           tmp.children.forEach(v -> stack.push(v));//压栈
       }
       //返回结果
       return list;
   }
}

递归版

1
2
3
4
5
6
7
8
9
10
11
class Solution {
    List<Integer> ans = new ArrayList<>();
    public List<Integer> preorder(Node root) {
        if(root==null)return new ArrayList<>();
        ans.add(root.val);
        for(int i=0;i<root.children.size();i++){
            preorder(root.children.get(i));
        }
        return ans;
    }
}

559. N 叉树的最大深度

1
2
3
4
5
6
7
8
9
10
class Solution {
    public int maxDepth(Node root) {
        if(root==null)return 0;
        int max = 0;
        for(Node node:root.children){
            max = Math.max(max,maxDepth(node));
        }
        return max + 1;
    }
}

429. N 叉树的层序遍历（mid）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    //BFS
    public List<List<Integer>> levelOrder(Node root) {
        List<List<Integer>> ret = new ArrayList<>();
        if(root==null)return ret;
        LinkedList<Node> queue = new LinkedList<>();
        queue.offer(root);
        while(!queue.isEmpty()){
            int size = queue.size();
            List<Integer> list = new ArrayList<>();
            for(int i=0;i<size;i++){
                Node node = queue.pop();
                list.add(node.val);
                if(node.children!=null&&node.children.size()>0)queue.addAll(node.children);
            }
            ret.add(list);
        }
        return ret;
    }
}

最大二叉树(中等)

最大二叉树

给定一个不含重复元素的整数数组。一个以此数组构建的最大二叉树定义如下：

二叉树的根是数组中的最大元素。 左子树是通过数组中最大值左边部分构造出的最大二叉树。 右子树是通过数组中最大值右边部分构造出的最大二叉树。 通过给定的数组构建最大二叉树，并且输出这个树的根节点。

示例 ：

1
2
3
4
5
6
7
8
9
10
输入：[3,2,1,6,0,5]
输出：返回下面这棵树的根节点：

      6
    /   \
   3     5
    \    / 
     2  0   
       \
        1

提示：给定的数组的大小在 [1, 1000] 之间。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    public TreeNode constructMaximumBinaryTree(int[] nums) {
        int n = nums.length;
        return build(nums,0,n-1);
    }
    public TreeNode build(int[] nums,int start,int end){
        if(start>end)return null;
        int maxIndex = start;
        for(int i=start+1;i<=end;i++)if(nums[i]>nums[maxIndex])maxIndex=i;
        TreeNode ret = new TreeNode(nums[maxIndex]);
        ret.left = build(nums,start,maxIndex-1);
        ret.right = build(nums,maxIndex+1,end);
        return ret;
    }
}

最大二叉树 II(中等)

最大树定义：一个树，其中每个节点的值都大于其子树中的任何其他值。

给出最大树的根节点 root。

就像之前的问题那样，给定的树是从表 A（root = Construct(A)）递归地使用下述 Construct(A) 例程构造的：

如果 A 为空，返回 null 否则，令 A[i] 作为 A 的最大元素。创建一个值为 A[i] 的根节点 root root 的左子树将被构建为 Construct([A[0], A[1], …, A[i-1]])
root 的右子树将被构建为 Construct([A[i+1], A[i+2], …, A[A.length - 1]])
返回 root 请注意，我们没有直接给定 A，只有一个根节点 root = Construct(A).

假设 B 是 A 的副本，并附加值 val。保证 B 中的值是不同的。

返回 Construct(B)。

示例 1：

输入：root = [4,1,3,null,null,2], val = 5 输出：[5,4,null,1,3,null,null,2]
解释：A = [1,4,2,3], B = [1,4,2,3,5]
示例 2：

输入：root = [5,2,4,null,1], val = 3 输出：[5,2,4,null,1,null,3]
解释：A = [2,1,5,4], B = [2,1,5,4,3]
示例 3：

输入：root = [5,2,3,null,1], val = 4 输出：[5,2,4,null,1,3]
解释：A = [2,1,5,3], B = [2,1,5,3,4]

提示：

1 <= B.length <= 100

二叉搜索树的第k大节点(简单)

给定一棵二叉搜索树，请找出其中第k大的节点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
示例 1:

输入: root = [3,1,4,null,2], k = 1
   3
  / \
 1   4
  \
   2
输出: 4
示例 2:

输入: root = [5,3,6,2,4,null,null,1], k = 3
       5
      / \
     3   6
    / \
   2   4
  /
 1
输出: 4

限制： 1 ≤ k ≤ 二叉搜索树元素个数

解题思路

二叉搜索树、通过中许遍历得到递增序列、那么优先改变一下，从右子树先遍历即可得到递减序列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution {
    //递归中序
    private int ans = 0, count = 0;
    public int kthLargest(TreeNode root, int k) {
        // clarification:  root == null?   k <= 1?
        helper(root, k);
        return ans;
    }
    private void helper(TreeNode root, int k) {
        if (root.right != null) helper(root.right, k);
        if (++count == k) {
            ans = root.val;
            return;
        }
        if (root.left != null) helper(root.left, k);
    }
    //中序遍历
    public int kthLargest(TreeNode root, int k) {
        List<Integer> list = new ArrayList<>();
        Stack<TreeNode> stack = new Stack<>();
        if(root==null)return 0;
        while(root!=null||!stack.isEmpty()){
            while(root!=null){
                stack.push(root);
                root = root.left;
            }
            if(!stack.isEmpty()){
                TreeNode p = stack.pop();
                list.add(p.val);
                root = p.right;
            }
        }
        return list.get(list.size()-k);
    }
}

230. 二叉搜索树中第K小的元素（mid）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    //思路：中序遍历得出递增序列
    int ret;
    int count;
    public int kthSmallest(TreeNode root, int k) {
        dfs(root,k);
        return ret;
    }
    public void dfs(TreeNode root,int k){
        if(root.left!=null)dfs(root.left,k);
        if(++count==k){
            ret = root.val;
            return;
        }
        if(root.right!=null)dfs(root.right,k);
    }
}

好叶子节点对的数量(中等)

给你二叉树的根节点 root 和一个整数 distance 。

如果二叉树中两个 叶 节点之间的 最短路径长度 小于或者等于 distance ，那它们就可以构成一组 好叶子节点对 。

返回树中 好叶子节点对的数量 。

示例

1
2
3
4
5
6
7
8
输入: root = [1,2,3,null,4], distance = 3
       1
      / \
     2   3
      \
       4
输出: 1
解释：树的叶节点是 3 和 4 ，它们之间的最短路径的长度是 3 。这是唯一的好叶子节点对。

解题思路

父节点和子节点的距离是 1

对树后序遍历 ，需要返回这个节点到其下方所有叶子节点的距离

这样就可以将这个节点的左子树所有叶子节点和右子树所有叶子节点都凑个对

然后将所有叶子节点不超过距离的弄到一起返回

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
class Solution {
    //计数
    private int ans = 0;

    public int countPairs(TreeNode root, int distance) {
        dfs(root, distance);
        return ans;
    }

    //后续遍历
    private List<Integer> dfs(TreeNode root, int distance) {
        //当前节点为空返回空
        if (root == null)
            return new ArrayList();
        //叶子节点
        if (root.left == null && root.right == null) {
            List<Integer> list = new ArrayList();
            list.add(0);
            return list;
        }
        //
        List<Integer> list = new ArrayList();
        //左叶子节点的距离
        List<Integer> left = dfs(root.left, distance);
        //判断是否超过distance
        for (int it : left) {
            if (++it > distance)
                continue;
            list.add(it);
        }
        //右叶子节点的距离
        List<Integer> right = dfs(root.right, distance);
        for (int it : right) {
            if (++it > distance)
                continue;
            list.add(it);
        }
        //
        for (int l : left) {
            for (int r : right) {
                if (l + r + 2 <= distance)
                    ans++;
            }
        }
        return list;
    }
}

具有所有最深节点的最小子树(中等)

题目描述

给定一个根为 root 的二叉树，每个节点的深度是 该节点到根的最短距离 。 如果一个节点在 整个树 的任意节点之间具有最大的深度，则该节点是 最深的 。 一个节点的 子树 是该节点加上它的所有后代的集合。 返回能满足 以该节点为根的子树中包含所有最深的节点 这一条件的具有最大深度的节点。

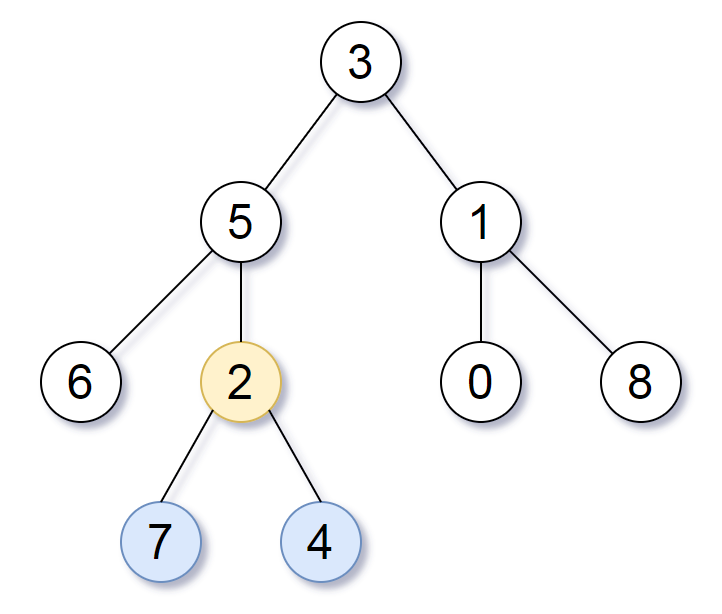
说的云里雾里，人话：最深叶子节点的最近公共祖先

输入：root = [3,5,1,6,2,0,8,null,null,7,4]
输出：[2,7,4]
解释： 我们返回值为 2 的节点，在图中用黄色标记。 在图中用蓝色标记的是树的最深的节点。 注意，节点 5、3 和 2 包含树中最深的节点，但节点 2 的子树最小，因此我们返回它。

解题思路

对于一个节点，如果左子树高度==右子树高度，这个节点就是答案，如果左子树高度<右子树高度，查找右子树，否则查找左子树

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    public TreeNode subtreeWithAllDeepest(TreeNode root) {
        if (root == null) return null;//为空返回
        else {
            int ldep = maxDepth(root.left), rdep = maxDepth(root.right);//获取左右最大深度
            if (ldep == rdep) return root;//相等返回
            else if (ldep > rdep) return subtreeWithAllDeepest(root.left);//左边深度大、查找左边
            else return subtreeWithAllDeepest(root.right);//右边深度大、查找右边
        }
    }

    int maxDepth(TreeNode root) {//获取当前节点的最大深度
        if (root == null) return 0;
        else return Math.max(maxDepth(root.left), maxDepth(root.right)) + 1;
    }
}

求和路径(中等)

题目描述

给定一棵二叉树，其中每个节点都含有一个整数数值(该值或正或负)。设计一个算法，打印节点数值总和等于某个给定值的所有路径的数量。注意，路径不一定非得从二叉树的根节点或叶节点开始或结束，但是其方向必须向下(只能从父节点指向子节点方向)。

示例:
给定如下二叉树，以及目标和 sum = 22，

1
2
3
4
5
6
7
      5
     / \
    4   8
   /   / \
  11  13  4
 /  \    / \
7    2  5   1

返回:3 解释：和为 22 的路径有：[5,4,11,2], [5,8,4,5], [4,11,7]
提示：节点总数 <= 10000

解题思路

求出当前节点为根路径是否满足，递归判断每个节点

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    int count = 0;

    public int pathSum(TreeNode root, int sum) {
        if (root == null) return 0;
        helper(root, sum);
        if (root.left != null) pathSum(root.left, sum);
        if (root.right != null) pathSum(root.right, sum);
        return count;
    }


    public void helper(TreeNode node, int sum) {
        if (sum == node.val) count++;
        if (node.left != null) helper(node.left, sum - node.val);
        if (node.right != null) helper(node.right, sum - node.val);
    }
}

二叉树的层序遍历(中等)

给你一个二叉树，请你返回其按 层序遍历 得到的节点值。 （即逐层地，从左到右访问所有节点）。

解题思路

广度优先遍历，采用队列获取其每层的长度

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> result = new ArrayList<>();
        Queue<TreeNode> queue = new LinkedList<>();
        List<Integer> list;
        if (!Objects.isNull(root)) queue.add(root);
        while (!queue.isEmpty()) {
            int size = queue.size();
            list = new ArrayList<>();
            for (int i = 0; i < size; i++) {
                TreeNode node = queue.poll();
                list.add(node.val);
                if (node.left != null) queue.add(node.left);
                if (node.right != null) queue.add(node.right);
            }
            result.add(list);
        }
        return result;
    }
}

107. 二叉树的层序遍历 II

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    //bfs
    public List<List<Integer>> levelOrderBottom(TreeNode root) {
        List<List<Integer>> ret = new ArrayList<>();
        if(root==null)return ret;
        LinkedList<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        while(!queue.isEmpty()){
            int size = queue.size();
            List<Integer> list = new ArrayList<>();
            for(int i=0;i<size;i++){
                TreeNode p = queue.pop();
                list.add(p.val);
                if(p.left!=null)queue.offer(p.left);
                if(p.right!=null)queue.offer(p.right);
            }
            ret.add(list);
        }
        Collections.reverse(ret);
        return ret;
    }
}

二叉树的最近公共祖先(中等)

解题思路

对树DFS判断其目标节点是否存在，如果存在返回true寻找另一个节点，当两个节点都找到，递归返回获得其第一个公共节点

1
2
3
4
5
6
7
8
9
class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(root == null || p == root || q == root)return root;//递归结束条件
        TreeNode left = lowestCommonAncestor(root.left,p,q);//深度优先遍历左子树
        TreeNode right = lowestCommonAncestor(root.right,p,q);//深度优先遍历右子树
        if(left!=null && right != null)return root;//找到节点将其返回
        return left == null ? right : left;//否则返回已查询到的节点
    }
}

235. 二叉搜索树的最近公共祖先（easy)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    //根据二叉搜索树的性质root.left<root<root.right,可知父节点为root.val
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        TreeNode ancestor = root;
        while (true) {
            if (p.val < ancestor.val && q.val < ancestor.val) {//pq都小于root在左子树
                ancestor = ancestor.left;
            } else if (p.val > ancestor.val && q.val > ancestor.val) {//pq都大于root在右子树
                ancestor = ancestor.right;
            } else {//等于其中一个或者呈递增序列则直接返回
                break;
            }
        }
        return ancestor;
    }
    //直接搜索
    public TreeNode lowestCommonAncestor0(TreeNode root, TreeNode p, TreeNode q) {
        if(root==q||root==p||root==null)return root;
        TreeNode left = lowestCommonAncestor(root.left,p,q);
        TreeNode right = lowestCommonAncestor(root.right,p,q);
        if(left!=null&&right!=null)return root;
        return left!=null?left:right;
    }
}

二叉树的直径(容易)

题目描述

给定一棵二叉树，你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。

示例 :
给定二叉树

1
2
3
4
5
    1
   / \
  2   3
 / \     
4   5

返回 3, 它的长度是路径 [4,2,1,3] 或者 [5,2,1,3]。

注意：两结点之间的路径长度是以它们之间边的数目表示。

解题思路

深度优先搜索，分别递归计算每个节点的左右子树的路径之和，默认值为1超过则更新，递归向上执行

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    int ans;//记录最大路径

    public int diameterOfBinaryTree(TreeNode root) {//方法入口
        ans = 1;
        depth(root);
        return ans - 1;
    }

    //深度优先遍历
    public int depth(TreeNode node) {
        if (node == null) return 0; // 访问到空节点了，返回0
        int L = depth(node.left); // 左儿子为根的子树的深度
        int R = depth(node.right); // 右儿子为根的子树的深度
        ans = Math.max(ans, L + R + 1); // 计算d_node即L+R+1 并更新ans
        return Math.max(L, R) + 1; // 返回该节点为根的子树的深度
    }
}

二叉树的锯齿形层次遍历(中等)

题目描述

给定一个二叉树，返回其节点值的锯齿形层次遍历。（即先从左往右，再从右往左进行下一层遍历，以此类推，层与层之间交替进行）。

例如： 给定二叉树 [3,9,20,null,null,15,7],

1
2
3
4
5
 3
/ \
9 20 
 /  \
 15 7

返回锯齿形层次遍历如下：

[
[3],
[20,9],
[15,7]
]

解题思路

广度优先遍历，每次将当前层元素出队，使用一个全局变量判断方向，调用addLast或者addFirst。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
class Solution {
    public void DFS(TreeNode node, int level, List<List<Integer>> results) {
        if (level >= results.size()) {
            LinkedList<Integer> newLevel = new LinkedList<Integer>();
            newLevel.add(node.val);
            results.add(newLevel);
        } else {
            if (level % 2 == 0)
                results.get(level).add(node.val);
            else
                results.get(level).add(0, node.val);
        }

        if (node.left != null) DFS(node.left, level + 1, results);
        if (node.right != null) DFS(node.right, level + 1, results);
    }

    public List<List<Integer>> zigzagLevelOrder(TreeNode root) {
        if (root == null) {
            return new ArrayList<List<Integer>>();
        }
        List<List<Integer>> results = new ArrayList<List<Integer>>();
        DFS(root, 0, results);
        return results;
    }
    //
    public List<List<Integer>> zigzagLevelOrder(TreeNode root) {
        List<List<Integer>> ant = new LinkedList<>();
        if(root==null)return ant;
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        boolean flag = false;
        while(!queue.isEmpty()){
            int size = queue.size();
            List<Integer> list = new LinkedList<>();
            for(int i=0;i<size;i++){
                TreeNode node = queue.poll();
                list.add(node.val);
                if(node.left!=null)queue.offer(node.left);
                if(node.right!=null)queue.offer(node.right);
            }
            if(flag)
            Collections.reverse(list);
            ant.add(list);
            flag=!flag;
        }
        return ant;
    }
}

二叉树的最大深度(简单)

解题思路

递归每次递归返回+1,返回左右节点较大的值。

代码实现

1
2
3
4
5
6
class Solution {
    public int maxDepth(TreeNode root) {
        if (Objects.isNull(root)) return 0;
        return Math.max(maxDepth(root.left), maxDepth(root.right)) + 1;
    }
}

二叉树的最小深度（easy)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public int minDepth(TreeNode root) {
    if (root == null) {
        return 0;
    }
    // null节点不参与比较
    if (root.left == null && root.right != null) {
        return 1 + minDepth(root.right);
    }
    // null节点不参与比较
    if (root.right == null && root.left != null) {
        return 1 + minDepth(root.left);
    }
    	return 1 + Math.min(minDepth(root.left), minDepth(root.right));
    }
}

验证二叉搜索树(中等)

题目描述

给定一个二叉树，判断其是否是一个有效的二叉搜索树。

假设一个二叉搜索树具有如下特征：

  • 节点的左子树只包含小于当前节点的数。
  • 节点的右子树只包含大于当前节点的数。
  • 所有左子树和右子树自身必须也是二叉搜索树。

示例 1:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
输入:
     2
    / \
   1   3
输出: true
示例 2:
 
输入:
     5
    / \
   1   4
      / \
     3   6
输出: false

解释: 输入为: [5,1,4,null,null,3,6]。 根节点的值为 5 ，但是其右子节点值为 4 。

解题思路

获取左右子书的边界值，递归判断每一个节点是否满足条件

代码实现

1
2
3
4
5
6
7
8
9
10
11
class Solution {
    public boolean isValidBST(TreeNode root) {
        return dfs(root,Long.MAX_VALUE,Long.MIN_VALUE);
    }
    //左子树小于max,右子树都要大于min,注意使用long
    public boolean dfs(TreeNode root,long max,long min){
        if(root==null)return true;
        if(root.val>=max||root.val<=min)return false;
        return dfs(root.left,root.val,min) && dfs(root.right,max,root.val);
    }
}

二叉树中的最大路径和(困难)

题目描述

给定一个非空二叉树，返回其最大路径和。

思路

后序递归遍历，判断其左右子树最大值，依此递归

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    //思路：自底向上（后序）递归的计算左右子树和根节点的和，记录其大小
    int ans = Integer.MIN_VALUE;//记录结果
    public int maxPathSum(TreeNode root) {
        max(root);
        return ans;
    }
    //后序遍历
    public int max(TreeNode root) {
        if (Objects.isNull(root)) return 0;//递归结束
        int left = Math.max(max(root.left), 0);//左子树最大值（负数直接不取，所以和0比较）
        int right = Math.max(max(root.right), 0);//右子树最大值（负数直接不取，所以和0比较）
        ans = Math.max(ans, left + right + root.val);//是否大于当前的最大值
        return Math.max(left, right) + root.val;//返回最大值
    }
}

从前序与中序遍历序列构造二叉树(中等)

根据一棵树的前序遍历与中序遍历构造二叉树。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
preorder = [3,9,20,15,7]
inorder = [9,3,15,20,7]
首先根据 preorder 找到根节点是 3
    
然后根据根节点将 inorder 分成左子树和右子树
左子树
inorder [9]

右子树
inorder [15,20,7]

把相应的前序遍历的数组也加进来
左子树
preorder[9] 
inorder [9]

右子树
preorder[20 15 7] 
inorder [15,20,7]

现在我们只需要构造左子树和右子树即可，成功把大问题化成了小问题
然后重复上边的步骤继续划分，直到 preorder 和 inorder 都为空，返回 null 即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        HashMap<Integer, Integer> map = new HashMap<>();//存储值对应的下标
        for (int i = 0; i < inorder.length; i++)map.put(inorder[i], i);//存入map
        return buildTree(preorder,0,preorder.length-1,inorder,0,inorder.length-1,map);//递归调用
    }
    //构建
    TreeNode buildTree(int[] preorder, int preStart, int preEnd,int[] inorder, int inStart, int inEnd, Map<Integer, Integer> inMap) {
        if(preStart > preEnd || inStart > inEnd) return null;//下标超过则停止(递归结束条件)
        TreeNode root = new TreeNode(preorder[preStart]);//构建结点
        int inRoot = inMap.get(root.val);//根结点下标
        int numsLeft = inRoot - inStart;//重新定义左边(左子树有多少个节点)
        root.left = buildTree(preorder, preStart + 1, preStart + numsLeft,inorder, inStart, inRoot - 1, inMap);//递归调用
        root.right = buildTree(preorder, preStart + numsLeft + 1, preEnd,inorder, inRoot + 1, inEnd, inMap);//递归调用
        return root;//返回根节点
    }
}

从中序与后序遍历序列构造二叉树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
    //思路：递归
    //遍历指的是根节点遍历的顺序
    //后序中最后一个节点为根节点，中序根节点左边全部为根节点左子树，递归缩小范围
    public TreeNode buildTree(int[] inorder, int[] postorder) {
        Map<Integer,Integer> map = new HashMap<>();
        for(int i=0;i<inorder.length;i++)map.put(inorder[i],i);
        return buildTree(inorder,0,inorder.length-1,postorder,0,postorder.length-1,map);
    }
    public TreeNode buildTree(int[] inorder,int inStart,int inEnd, int[] postorder,int postStart,int postEnd,Map<Integer,Integer> map){
        if(inStart>inEnd||postStart>postEnd)return null;
        TreeNode node = new TreeNode(postorder[postEnd]);
        int index = map.get(node.val);//获取当前根节点所在中序数组的位置
        int num = index - inStart;//当前左子树的节点数量
        //递归构建左子树: 
        //此时中序范围为inStart到当前节点在中序数组中的位置减一,即[inStart,index-1]
        //因为后续遍历最后一个值为根节点，此时后续范围开始下标为postStart,结束下标为当前后续开始下标+左子树还有的节点数量-1,即[postStart,postStart+num-1]
        node.left = buildTree(inorder,inStart,index-1,postorder,postStart,postStart+num-1,map);
        //递归构建右子树:
        //此时中序范围为当前节点在中序数组中的位置加一到inEnd,即[index+1,inEnd]
        //此时后续遍历的开始为上面左子树的结束+1,即 postStart+num ,结束为postEnd-1,减一是因为当前节点已经作为根节点使用
        node.right = buildTree(inorder,index+1,inEnd,postorder,postStart+num,postEnd-1,map);
        return node;
    }
}

889. 根据前序和后序遍历构造二叉树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
    public TreeNode constructFromPrePost(int[] preorder, int[] postorder) {
        int m = preorder.length;
        int n = postorder.length;
        Map<Integer,Integer> postMap = new HashMap<>();
        for (int i = 0; i < n; i++) postMap.put(postorder[i],i);
        return buildTree(preorder,0,m-1,postorder,0,n-1,postMap);
    }
    //preorder = [1,2,4,5,3,6,7], postorder = [4,5,2,6,7,3,1]
    //root=1  root.left=2 [4,5]  root.right=3 [6,7]
    //先序: 根左右
    //后序: 左右根
    //思路：每次获取先序数组第一个节点作为根节点root
    //因为先序是[根左右],所以先序的列表中顺数第二个节点必定为当前根节点左子树节点left,所以在后序列表中left所在位置左边都是left的左子树
    //因为后序是[左右根],所以在后序列表中倒数第二个节点必定为当前根节点右子树节点right,所以在先序列表中right所在位置右边都是right的左子树
    public TreeNode buildTree(int[] preorder,int preStart,int preEnd, int[] postorder,int postStart,int postEnd,Map<Integer,Integer> postMap){
        if (preStart>preEnd||postStart>postEnd)return null;
        TreeNode newNode = new TreeNode(preorder[preStart]);
        if (preStart==preEnd)return newNode;//相等没有左右子树
        int index = postMap.get(preorder[preStart+1]);//当前newNode的左子树在后序中的位置
        int num = index-postStart;//newNode的左子树的个数
        newNode.left = buildTree(preorder,preStart+1,preStart+num+1,postorder,postStart,index,postMap);
        newNode.right = buildTree(preorder,preStart+num+2,preEnd,postorder,index+1,postEnd-1,postMap);
        return newNode;
    }
}

不同的二叉搜索树 II(中等)

解题思路

回溯

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
    public List<TreeNode> generateTrees(int n) {
        if (n == 0) {
            return new LinkedList<TreeNode>();
        }
        return generateTrees(1, n);
    }

    public List<TreeNode> generateTrees(int start, int end) {
        List<TreeNode> allTrees = new LinkedList<TreeNode>();
        if (start > end) {
            allTrees.add(null);
            return allTrees;
        }

        // 枚举可行根节点
        for (int i = start; i <= end; i++) {
            // 获得所有可行的左子树集合
            List<TreeNode> leftTrees = generateTrees(start, i - 1);
            // 获得所有可行的右子树集合
            List<TreeNode> rightTrees = generateTrees(i + 1, end);
            // 从左子树集合中选出一棵左子树，从右子树集合中选出一棵右子树，拼接到根节点上
            for (TreeNode left : leftTrees) {
                for (TreeNode right : rightTrees) {
                    TreeNode currTree = new TreeNode(i);
                    currTree.left = left;
                    currTree.right = right;
                    allTrees.add(currTree);
                }
            }
        }
        return allTrees;
    }
}

二叉树的右视图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    //bfs取每一层的最右边节点
    public List<Integer> rightSideView(TreeNode root) {
        List<Integer> ans = new ArrayList<>();
        Queue<TreeNode> queue = new LinkedList<>();
        if(root!=null)queue.offer(root);
        while(!queue.isEmpty()){
            int size = queue.size();
            for(int i=0;i<size;i++){
                TreeNode node = queue.poll();
                if(i==size-1)ans.add(node.val);
                if(node.left!=null)queue.offer(node.left);
                if(node.right!=null)queue.offer(node.right);
            }
        }
        return ans;
    }
}

求根节点到叶节点数字之和

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    public int sumNumbers(TreeNode root) {
        return dfs(root, 0);
    }
    public int dfs(TreeNode root, int prevSum) {
        if (root == null) {
            return 0;
        }
        int sum = prevSum * 10 + root.val;
        if (root.left == null && root.right == null) {
            return sum;
        } else {
            return dfs(root.left, sum) + dfs(root.right, sum);
        }
    }
}

路径总和(easy)

1
2
3
4
5
6
7
8
9
10
11
class Solution {
    //思路：dfs
    public boolean hasPathSum(TreeNode root, int targetSum) {
        return dfs(root,targetSum);
    }
    public boolean dfs(TreeNode root, int targetSum){
        if(root==null)return false;
        if(root.left==null&&root.right==null&&targetSum-root.val==0)return true;
        return dfs(root.left,targetSum-root.val)||dfs(root.right,targetSum-root.val);
    }
}

路径总和 II

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    //思路:dfs
    private List<List<Integer>> ans = new ArrayList<>();
    public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
        dfs(root,targetSum,new LinkedList<Integer>());
        return ans;
    }
    public void dfs(TreeNode root, int targetSum,LinkedList<Integer> path){
        if(root==null)return;
        path.add(root.val);
        int val = targetSum-root.val;
        if(root.left==null&&root.right==null&&val==0){
            ans.add(new ArrayList(path));
        }
        if(root.left!=null){
            dfs(root.left,val,path);
            path.removeLast();
        }
        if(root.right!=null){
            dfs(root.right,val,path);
            path.removeLast();
        }
    }
}

437. 路径总和 III

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
    //前缀和
    public int pathSum(TreeNode root, int targetSum) {
        HashMap<Long, Integer> prefix = new HashMap<>();
        prefix.put(0L, 1);
        return dfs(root, prefix, 0, targetSum);
    }
    public int dfs(TreeNode root, Map<Long, Integer> prefix, long curr, int targetSum) {
        if (root == null)  return 0;
        int ret = 0;
        curr += root.val;
        ret = prefix.getOrDefault(curr - targetSum, 0);
        prefix.put(curr, prefix.getOrDefault(curr, 0) + 1);
        ret += dfs(root.left, prefix, curr, targetSum);
        ret += dfs(root.right, prefix, curr, targetSum);
        prefix.put(curr, prefix.getOrDefault(curr, 0) - 1);
        return ret;
    }
    //思路:dfs
    int ret;
    public int pathSumDFS(TreeNode root, int targetSum) {
        if(root==null)return ret;
        dfs(root,0,targetSum);
        pathSum(root.left,targetSum);
        pathSum(root.right,targetSum);
        return ret;
    }
    public void dfs(TreeNode root,int v,int targetSum){
        v+=root.val;
        if(v==targetSum)ret++;
        if(root.left!=null)dfs(root.left,v,targetSum);
        if(root.right!=null)dfs(root.right,v,targetSum);       
    }
}

翻转二叉树（easy）

1
2
3
4
5
6
7
8
9
10
class Solution {
    //思路：递归翻转左右子树
    public TreeNode invertTree(TreeNode root) {
        if(root==null||(root.left==null&&root.right==null))return root;
        TreeNode left = root.left;
        root.left = invertTree(root.right);
        root.right = invertTree(left);
        return root;
    }
}

对称二叉树

1
2
3
4
5
6
7
8
9
10
11
class Solution {
    //思路:递归交替判断
    public boolean isSymmetric(TreeNode root) {
        return dfs(root.left,root.right);
    }
    public boolean dfs(TreeNode left,TreeNode right){
        if(left==null&&right==null)return true;
        if(left==null||right==null)return false;
        return left.val==right.val && dfs(left.right,right.left) && dfs(left.left,right.right);
    }
}

二叉搜索树与双向链表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
    //思路：中序遍历
    Node pre, head;//记录前置节点和头结点
    public Node treeToDoublyList(Node root) {
        if(root == null) return null;//空直接返回
        dfs(root);//
        head.left = pre;//处理头结点
        pre.right = head;
        return head;
    }
    //dfs(cur): 递归法中序遍历；
    //终止条件： 当节点 cur 为空，代表越过叶节点，直接返回；
    //递归左子树，即 dfs(cur.left) 
    //构建链表：
    //当 pre 为空时： 代表正在访问链表头节点，记为 head 
    //当 pre 不为空时： 修改双向节点引用，即 pre.right = cur ， cur.left = pre 
    //保存 cur ： 更新 pre = cur ，即节点 cur 是后继节点的 pre 
    //递归右子树，即 dfs(cur.right) 
    void dfs(Node cur) {
        if(cur == null) return;
        dfs(cur.left);//先遍历左结点
        if(pre != null) pre.right = cur;//如果有前驱节点则前驱节点right(下一个节点)执行当前节点
        else head = cur;//记录头结点
        cur.left = pre;//当前节点的left指向pre
        pre = cur;//更新前驱节点
        dfs(cur.right);//后遍历右边节点
    }
}

二叉树的完全性检验

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
     //完全二叉树bfs时null总会在队尾,如果存在队列中间有null则非完全二叉树
    public boolean isCompleteTree(TreeNode root) {
        LinkedList<TreeNode> q = new LinkedList<>();
        TreeNode cur;
        q.addLast(root);
        while ((cur = q.removeFirst()) != null) {
        		//无需做判断是空，方便后面判断
            q.addLast(cur.left);
            q.addLast(cur.right);
        }
        //如果是完全二叉树此时queue尾部装都为null
        //非完全会出现[node1,node2,null,node3]的情况
        while (!q.isEmpty()) {
            if (q.removeLast() != null) {
                return false;
            }
        }
        return true;
    }
}

实现 Trie (前缀树)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
class Trie {
    class TrieNode{
        TrieNode[] next = new TrieNode[26];
        boolean isEnd = false;
    }
    TrieNode root;

    public Trie() {
        root = new TrieNode();
    }
    
    public void insert(String word) {
        TrieNode cur = root;
        for(int i=0;i<word.length();i++){
            int index = word.charAt(i)-'a';
            if(cur.next[index]==null){
                cur.next[index] = new TrieNode();
            }
            cur = cur.next[index];
        }
        cur.isEnd = true;
    }
    
    public boolean search(String word) {
        TrieNode cur = root;
        for(int i=0;i<word.length();i++){
            int index = word.charAt(i)-'a';
            if(cur.next[index]==null)return false;
            cur = cur.next[index];
        }
        return cur.isEnd;
    }
    
    public boolean startsWith(String prefix) {
        TrieNode cur = root;
        for(int i=0;i<prefix.length();i++){
            int index = prefix.charAt(i)-'a';
            if(cur.next[index]==null)return false;
            cur = cur.next[index];
        }
        return true;
    }
}

二叉树最大宽度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
class Solution {
    //思路：BFS
    // 完全二叉树的性质）：对于一颗完全二插树，如果按照从上至下，从左往右对所有节点从零开始顺序编号
    // 则父节点的左孩子节点的序号：2*i+1   父节点的左孩子节点的序号：2*i+2;
    // 所以每层的宽度就可以使用：每层最后一个节点的值减去最后一个节点的值+1
    //       1
    //     /   \
    //    2     3
    //   / \   / \
    //  4   5 6   7
    public int widthOfBinaryTree(TreeNode root) {
        int ret = 0;
        LinkedList<TreeNode> queue = new LinkedList<>();
        root.val=0;//关键
        queue.offer(root);
        while(!queue.isEmpty()){
            int size = queue.size();
            //当前这层的宽度
            int width = queue.getLast().val-queue.getFirst().val+1;
            for(int i=0;i<size;i++){
                TreeNode node = queue.pop();
                if(node.left!=null){
                    node.left.val = 2 * node.val+1;//左子树编号
                    queue.offer(node.left);
                }
                if(node.right!=null){
                    node.right.val = 2 * node.val+2;//右子树编号
                    queue.offer(node.right);
                }
            }
            //更新宽度
            ret=Math.max(ret,width);
        }
        return ret;
    }
  	//DFS
		Map<Integer, Integer> levelMin = new HashMap<Integer, Integer>();
    public int widthOfBinaryTree(TreeNode root) {
        return dfs(root, 1, 1);
    }
    public int dfs(TreeNode node, int depth, int index) {
        if (node == null)return 0;
        levelMin.putIfAbsent(depth, index); // 每一层最先访问到的节点会是最左边的节点，即每一层编号的最小值
        return Math.max(index - levelMin.get(depth) + 1, 
        Math.max(dfs(node.left, depth + 1, index * 2), 
        dfs(node.right, depth + 1, index * 2 + 1)));
    }
}

二叉树的序列化与反序列化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
public class Codec {
    StringBuilder sb;
    //DFS遍历成字符串,当节点left和right为空记录为NULL
    public String serialize(TreeNode root) {
        sb = new StringBuilder();
        return reserialize(root);
    }
    public String reserialize(TreeNode root) {
        if(root==null)sb.append("NULL,");
        else{
            sb.append(root.val).append(",");
            reserialize(root.left);
            reserialize(root.right);
        }
        return sb.toString();
    }

    //递归解析树
    public TreeNode deserialize(String data) {
        String[] nodes = data.split(",");
        List<String> list = new LinkedList<>(Arrays.asList(nodes));
        return deserialize(list);
    }

    public TreeNode deserialize(List<String> list) {
        if("NULL".equals(list.get(0))){
            list.remove(0);
            return null;
        }
        TreeNode node = new TreeNode(Integer.valueOf(list.get(0)));
        list.remove(0);
        node.left = deserialize(list);
        node.right = deserialize(list);
        return node;
    }
}

449. 序列化和反序列化二叉搜索树（mid）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
public class Codec {
  // Encodes a tree to a list.
  public void postorder(TreeNode root, StringBuilder sb) {
    if (root == null) return;
    postorder(root.left, sb);
    postorder(root.right, sb);
    sb.append(intToString(root.val));
  }

  // Encodes integer to bytes string
  public String intToString(int x) {
    char[] bytes = new char[4];
    for(int i = 3; i > -1; --i) {
      bytes[3 - i] = (char) (x >> (i * 8) & 0xff);
    }
    return new String(bytes);
  }

  // Encodes a tree to a single string.
  public String serialize(TreeNode root) {
    StringBuilder sb = new StringBuilder();
    postorder(root, sb);
    return sb.toString();
  }

  // Decodes list to tree.
  public TreeNode helper(Integer lower, Integer upper, ArrayDeque<Integer> nums) {
    if (nums.isEmpty()) return null;
    int val = nums.getLast();
    if (val < lower || val > upper) return null;

    nums.removeLast();
    TreeNode root = new TreeNode(val);
    root.right = helper(val, upper, nums);
    root.left = helper(lower, val, nums);
    return root;
  }

  // Decodes bytes string to integer
  public int stringToInt(String bytesStr) {
    int result = 0;
    for(char b : bytesStr.toCharArray()) {
      result = (result << 8) + (int)b;
    }
    return result;
  }

  // Decodes your encoded data to tree.
  public TreeNode deserialize(String data) {
    ArrayDeque<Integer> nums = new ArrayDeque<Integer>();
    int n = data.length();
    for(int i = 0; i < (int)(n / 4); ++i) {
      nums.add(stringToInt(data.substring(4 * i, 4 * i + 4)));
    }

    return helper(Integer.MIN_VALUE, Integer.MAX_VALUE, nums);
  }
}

二叉树的镜像

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    //思路:dfs递归交换左右节点
    public TreeNode mirrorTree(TreeNode root) {
        dfs(root);
        return root;
    }
    public TreeNode dfs(TreeNode root){
        if(root==null)return root;
        TreeNode left = dfs(root.left);
        TreeNode right = dfs(root.right);
        root.left = right;
        root.right = left;
        return root;
    }
}

257. 二叉树的所有路径

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
    //直接回溯
    List<String> ret = new ArrayList<>();
    public List<String> binaryTreePaths(TreeNode root) {
        if(root==null)return ret;
        backtrack(root,new LinkedList<Integer>());
        return ret;
    }
    public void backtrack(TreeNode root,LinkedList<Integer> path){
        if(root==null)return;
        path.add(root.val);
        if(root.left==null&&root.right==null){
            StringBuilder sb = new StringBuilder();
            for(int i=0;i<path.size();i++){
                sb.append(path.get(i));
                if(i!=path.size()-1)sb.append("->");
            }
            ret.add(sb.toString());
        }
        if(root.left!=null){
            backtrack(root.left,path);
            path.removeLast();
        }
        if(root.right!=null){
            backtrack(root.right,path);
            path.removeLast();
        }
    }
}

另一棵树的子树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
    public boolean isSubtree(TreeNode root, TreeNode subRoot) {
        boolean ret = false;
        if(root==null)return false;
        if(root.val==subRoot.val)ret = compare(root,subRoot);
        return ret || isSubtree(root.left,subRoot)||isSubtree(root.right,subRoot);
    }
    public boolean compare(TreeNode p,TreeNode q){
        if(p==null||q==null)return p==q;
        if(p.val!=q.val)return false;
        return compare(p.left,q.left)&&compare(p.right,q.right);
    }
}

class Solution {
    private boolean isMatch;
    public boolean isSubtree(TreeNode root, TreeNode subRoot) {
        if(root.val==subRoot.val){
            if(dfs(root,subRoot))return true;
        }
        if(root.left!=null)isSubtree(root.left,subRoot);
        if(root.right!=null)isSubtree(root.right,subRoot);
        return isMatch;
    }
    public boolean dfs(TreeNode root, TreeNode subRoot){
        if(root==null&&subRoot==null)return true;
        if((root==null&&subRoot!=null)||(root!=null&&subRoot==null)||root.val!=subRoot.val)return false;
        return dfs(root.left,subRoot.left) && dfs(root.right,subRoot.right);
    }
}

440. 字典序的第K小数字（hard)

给定整数 n 和 k，返回 [1, n] 中字典序第 k 小的数字。

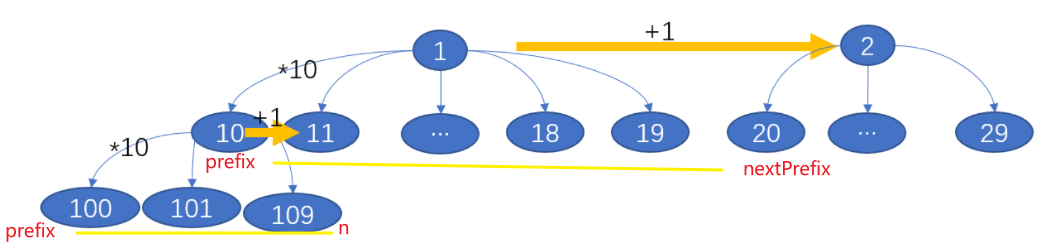
不难发现其实字典序就是对这棵十叉树进行**先序遍历**得出，1，10，100，101….,110,111,……，先序遍历到k-n节点即是目标值。

实际上我们求出第k小的数需要解决的问题如下：

1.怎么确定一个前缀下所有子节点的个数？

2.如果第 k 个数在当前的前缀下，怎么继续往下面的子节点找？

3.如果第 k 个数不在当前的前缀，即当前的前缀比较小，如何扩大前缀，增大寻找的范围？

其实就是需要确定往数的下走还是右走，从而确定目标值的位置

1.怎么确定一个前缀下所有子节点的个数？通过上图我们可以发现

1为前缀所有节点计算方式=(第1层nextPrefix-prifix)+(第2层nextPrefix-prifix)+…+(第n层nextPrefix-prifix)

那么问题又来了我怎么确定他是第几层呢？其实题目给我们的n就是说一共有n个字段序的数，那我们查找的前缀节点的值自然只能小于等于n，所以当我们的prifix大于n时我们就需要跳出层级节点计算了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
//计算prefix下的节点个数
public int getCount(int prefix,int n){
    //记录当前前缀
    long curr = prefix;//注意需要使用long来接收
    long next = prefix + 1;//下一个节点的前缀
    //记录峰头之间的累加
    int count = 0;
    while(curr<=n){
        //累加每层之间的差值
        //特别的 如果next已经大于n了的时候，因为要包含n 所以取n+1个数
        count+=Math.min(next,n+1)-curr;
        //进入下一层
        curr*=10;
        next*=10;
    }
    return count;
}

2.如果第 k 个数在当前的前缀下，怎么继续往下面的子节点找？

1
2
3
int count = getCount(prefix,n);//当前前缀下节点数
prefix*=10;//下沉一层
res++;//记录走过根节点

3.如果第 k 个数不在当前的前缀，即当前的前缀比较小，如何扩大前缀，增大寻找的范围？

1
2
3
int count = getCount(prefix,n);//当前前缀下节点数
prefix++;//前缀右移，1，2，3...
res+=getCount//走过当前前缀下所有节点

完整的代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
class Solution {
    //思路：构建为十叉树
    public int findKthNumber(int n, int k) {
        //初始化的时候包含1节点的，所以数量是1
        int res = 1;
        //默认是从1节点开始遍历，所以是1
        int prefix = 1;
        while(res<k){
            //计算当前分支下，如果跳到下一个峰，有多少节点数
            int count = getCount(prefix,n);
            //如果加上跨越到下一个峰的数量大于了目标k，则不能跳跃
            if(res+count>k){
                //走到下一层
                prefix*=10;
                //因为走过了根节点，所以需要加一
                res++;
            }else{
                //如果不大于的话直接加上走下一个分支
                res+=count;
                prefix++;
            }
        }
        return prefix;
    }
    //计算
    public int getCount(int prefix,int n){
        //记录当前前缀
        long curr = prefix;
        long next = prefix + 1;//下一个节点的前缀
        //记录峰头之间的累加
        int count = 0;
        while(curr<=n){
            //累加每层之间的差值
            //特别的 如果next已经大于n了的时候，因为要包含n 所以取n+1个数
            count+=Math.min(next,n+1)-curr;
            //进入下一层
            curr*=10;
            next*=10;
        }
        return count;
    }
}

删除二叉搜索树中的节点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
    //节点在的位置可能性
    //1.根节点()
    //2.叶子节点（直接删掉）
    //3.待删除的节点无左子树，有右子树
    //4.待删除的节点有左子树，无右子树
    //5.待删除的节点有左子树、右子树(左子树作为新的代替节点，右子树插入左子树最右边的节点)
    public TreeNode deleteNode(TreeNode root, int key) {
        //1
        if(root==null)return root;
        if(root.val>key){
            root.left = deleteNode(root.left,key);
        }else if(root.val<key){
            root.right = deleteNode(root.right,key);
        }else if(root.val == key){
            if(root.left==null&&root.right==null)return null;//2
            if(root.left==null&&root.right!=null)return root.right;//3
            if(root.left!=null&&root.right==null)return root.left;//4
            //5
            if(root.left!=null&&root.right!=null){
                //获取左子树的最右边节点
                TreeNode left = root.left;
                while(left.right!=null)left = left.right;
                left.right = root.right;
                return root.left;
            }
        }
        return root;
    }
}

二叉树展开为链表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
    //思路：递归先遍历左子树,设置其right,再返回其左子树最大节点
    public void flatten(TreeNode root) {
        if(root==null)return;//特殊条件
        recursion(root);//开始递归
    }
    public TreeNode recursion(TreeNode root) {
        TreeNode right = root.right;
        TreeNode left = root.left;
        if(root.left==null&&root.right==null)return root;//左子树最后一个节点直接返回
        TreeNode ret = null;//返回回来的最大节点
        //左子树还有节点优先进入递归
        if(root.left!=null){
            root.right = root.left;//可设置root.right为左子树
            ret = recursion(left);
        }
        //如果当前节点有左右子树，需要将左子树返回回来的节点作为最大节点设置right
        if(ret!=null && right!=null){
            ret.right = right;
            recursion(right);
        }
        //如果当前节点只要右子树，直接进入右子树递归
        if(right!=null)ret = recursion(right);
        root.left = null;//左子树置空
        return ret;//返回
    }
}

相同的树(easy)

1
2
3
4
5
6
7
8
class Solution {
    //递归遍历树
    public boolean isSameTree(TreeNode p, TreeNode q) {
        if(p==null||q==null)return p==q;
        if(p.val!=q.val) return false;
        return isSameTree(p.left,q.left)&&isSameTree(p.right,q.right);
    }
}

113. 二叉树中和为某一值的路径

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
    //思路：回溯
    private List<List<Integer>> ret;
    public List<List<Integer>> pathSum(TreeNode root, int target) {
        ret = new ArrayList<>();
        if(root==null)return ret;
        backtrack(root,new LinkedList<>(),target);
        return ret;
    }
    public void backtrack(TreeNode root,LinkedList<Integer> path, int target){
        path.add(root.val);
        target-=root.val;
        if(target==0&&root.left==null&&root.right==null){
            ret.add(new ArrayList(path));
            return;
        }
        if(root.left!=null){
            backtrack(root.left,path,target);
            path.removeLast();
        }
        if(root.right!=null){
            backtrack(root.right,path,target);
            path.removeLast();
        }
    }
}

108. 将有序数组转换为二叉搜索树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    //思路：递归每次取数组中间节点作为根节点，当left>right递归结束
    public TreeNode sortedArrayToBST(int[] nums) {
        return helper(nums, 0, nums.length - 1);
    }
    public TreeNode helper(int[] nums, int left, int right) {
        if (left > right) return null;
        // 总是选择中间位置左边的数字作为根节点
        int mid = (left + right) / 2;
        TreeNode root = new TreeNode(nums[mid]);
        root.left = helper(nums, left, mid - 1);
        root.right = helper(nums, mid + 1, right);
        return root;
    }
}

99. 恢复二叉搜索树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
class Solution {
    //O(n)中序遍历判断不是升序的两个节点进行交换
    public void recoverTreeOn(TreeNode root) {
        if(root==null)return;
        Stack<TreeNode> stack = new Stack<>();
        List<TreeNode> list = new ArrayList<>();
        while(root!=null||!stack.isEmpty()){
            while(root!=null){
                stack.push(root);
                root = root.left;
            }
            if(!stack.isEmpty()){
                root = stack.pop();
                list.add(root);
                root = root.right;
            }
        }
        //从前向后查找递减的那个数
        TreeNode val1=null;
        for(int i=0;i<list.size();i++){
            if(list.get(i).val>list.get(i+1).val){
                val1=list.get(i);
                break;
            }
        }
        //从后向前查找递减的那个数
        TreeNode val2=null;
        for(int i=list.size()-1;i>=0;i--){
            if(list.get(i).val<list.get(i-1).val){
                val2=list.get(i);
                break;
            }
        }
        int tmp = val1.val;
        val1.val = val2.val;
        val2.val = tmp;
    }
    //O(1) Morris 中序遍历
    public void recoverTree(TreeNode root) {
        TreeNode x = null, y = null, pred = null, predecessor = null;
        while (root != null) {
            if (root.left != null) {
                // predecessor 节点就是当前 root 节点向左走一步，然后一直向右走至无法走为止
                predecessor = root.left;
                while (predecessor.right != null && predecessor.right != root) {
                    predecessor = predecessor.right;
                }
                // 让 predecessor 的右指针指向 root，继续遍历左子树
                if (predecessor.right == null) {
                    predecessor.right = root;
                    root = root.left;
                }
                // 说明左子树已经访问完了，我们需要断开链接
                else {
                    if (pred != null && root.val < pred.val) {
                        y = root;
                        if (x == null) {
                            x = pred;
                        }
                    }
                    pred = root;
                    predecessor.right = null;
                    root = root.right;
                }
            }
            // 如果没有左孩子，则直接访问右孩子
            else {
                if (pred != null && root.val < pred.val) {
                    y = root;
                    if (x == null) {
                        x = pred;
                    }
                }
                pred = root;
                root = root.right;
            }
        }
        swap(x, y);
    }
    public void swap(TreeNode x, TreeNode y) {
        int tmp = x.val;
        x.val = y.val;
        y.val = tmp;
    }
}

116. 填充每个节点的下一个右侧节点指针（mid）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
    //dfs
    public Node connect(Node root) {
        if (root == null) return null;
        if (root.left != null) {
            root.left.next = root.right;
            if (root.next != null) {//跨父右节点next=父节点next左边节点
                root.right.next = root.next.left;
            }
        }
        connect(root.left);
        connect(root.right);
        return root;
    }
    //bfs
    public Node connectbfs(Node root) {
        LinkedList<Node> queue = new LinkedList<>();
        if(root==null)return root;
        queue.offer(root);
        while(!queue.isEmpty()){
            int size = queue.size();
            Node prev = null;
            for(int i=0;i<size;i++){
                Node node = queue.pop();
                if(prev!=null)prev.next = node;
                if(node.left!=null)queue.offer(node.left);
                if(node.right!=null)queue.offer(node.right);
                prev = node;
            }
        }
        return root;
    }
}

117. 填充每个节点的下一个右侧节点指针 II（mid）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
class Solution {
    //
    Node last = null, nextStart = null;
    public Node connect(Node root) {
        if (root == null) return null;
        Node start = root;
        while (start != null) {
            last = null;
            nextStart = null;
            for (Node p = start; p != null; p = p.next) {
                if (p.left != null) handle(p.left);
                if (p.right != null) handle(p.right);
            }
            start = nextStart;
        }
        return root;
    }
    public void handle(Node p) {
        if (last != null) last.next = p;
        if (nextStart == null) nextStart = p;
        last = p;
    }
    //BFS
    public Node connect(Node root) {
        if(root==null)return root;
        LinkedList<Node> queue = new LinkedList<>();
        queue.offer(root);
        while(!queue.isEmpty()){
            int size = queue.size();
            Node prev = null;
            for(int i=0;i<size;i++){
                Node node = queue.pop();
                if(prev!=null)prev.next = node;
                if(node.left!=null)queue.offer(node.left);
                if(node.right!=null)queue.offer(node.right);
                prev = node;
            }
            prev.next = null;
        }
        return root;
    }
}

222. 完全二叉树的节点个数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
class Solution {
    //O(1)解法
    //n层完全二叉树每层最多节点:1 2 4 8 = 2^n (下标从0开始)
    //1 3 7 15 = [2^n,2^(n+1)-1]
    //思路：通过二分查找，其节点值必在[2^n,2^(n+1)-1]区间内
    public int countNodes(TreeNode root) {
        if (root == null) return 0;
        int level = 0;
        TreeNode node = root;
        while (node.left != null) {//因为完全二叉树的节点主要集中在左边，可以通过遍历左子树确定层数
            level++;
            node = node.left;
        }
        //二分查找
        int low = 1 << level, high = (1 << (level + 1)) - 1;//[2^n,2^(n+1)-1]
        while (low < high) {
            int mid = (high - low + 1) / 2 + low;
            if (exists(root, level, mid)) {//mid存在靠右
                low = mid;
            } else {//否则在左区间
                high = mid - 1;
            }
        }
        return low;
    }
    //判断节点是否存在
    //     1            h = 0
    //    / \
    //   2   3          h = 1
    //  / \  /\
    // 4  5 6  7        h = 2
    //现在这个树中的值都是节点的编号，最底下的一层的编号是[2^h ，2^h - 1]，现在h = 2，也就是4, 5, 6, 7。
    //4, 5, 6, 7对应二进制分别为 100 101 110 111 不看最左边的1，从第二位开始，0表示向左，1表示向右，正好可以表示这个节点相对于根节点的位置。
    //比如4的 00 就表示从根节点 向左 再向左。6的 10 就表示从根节点 向右 再向左

    //那么想访问最后一层的节点就可以从节点的编号的二进制入手。从第二位开始的二进制位表示了最后一层的节点相对于根节点的位置。
    //那么就需要一个bits = 2^(h - 1) 上面例子中的bits就是2，对应二进制为010。这样就可以从第二位开始判断。（树三层高，需要向左或向右走两次才能到叶子）
    //比如看5这个节点存不存在，先通过位运算找到编号为5的节点相对于根节点的位置。010 & 101 发现第二位是0，说明从根节点开始，第一步向左走。
    //之后将bit右移一位，变成001。001 & 101 发现第三位是1，那么第二步向右走。
    //最后bit为0，说明已经找到编号为5的这个节点相对于根节点的位置，看这个节点是不是空，不是说明存在，exist返回真
    //编号为5的节点存在，说明总节点数量一定大于等于5。所以二分那里low = mid

    //再比如看7存不存在，010 & 111 第二位为1，第一部从根节点向右；001 & 111 第三位也为1，第二步继续向右。
    //然后判断当前节点是不是null，发现是null，exist返回假。
    //编号为7的节点不存在，说明总节点数量一定小于7。所以high = mid - 1
    public boolean exists(TreeNode root, int level, int k) {
        int bits = 1 << (level - 1);//最多有2^(n+1)-1
        TreeNode node = root;
        while (node != null && bits > 0) {
            if ((bits & k) == 0) {
                node = node.left;
            } else {
                node = node.right;
            }
            bits >>= 1;
        }
        return node != null;
    }
    //O(n)解法
    int ret;
    public int countNodesOn(TreeNode root) {
        if(root==null)return 0;
        return countNodes(root.left)+countNodes(root.right)+1;
    }
}

337. 打家劫舍 III

1

863. 二叉树中所有距离为 K 的结点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
    //思路：子树距离等于k可以很方便判断出，但是难点在通过父节点进行判断，所以通过map存储数节点的父节点
    //1.先序遍历得到target节点，查找其子树距离k的节点，在查找父亲节点距离k
    List<Integer> ret = new ArrayList<>();
    Map<Integer,TreeNode> parent = new HashMap<>();
    public List<Integer> distanceK(TreeNode root, TreeNode target, int k) {
        setParent(root);
        findAns(target,null,0,k);//直接从目标节点进行遍历
        return ret;
    }
    public void setParent(TreeNode root){
        if(root.left!=null){
            parent.put(root.left.val,root);
            setParent(root.left);
        }
        if(root.right!=null){
            parent.put(root.right.val,root);
            setParent(root.right);
        }
    }
    public void findAns(TreeNode root,TreeNode from,int depth,int k){
        if(root==null)return;
        if(depth==k){ret.add(root.val);return;}
        //左右子节点
        if(root.left!=from)findAns(root.left,root,depth+1,k);
        if(root.right!=from)findAns(root.right,root,depth+1,k);
        //父亲节点
        if(parent.get(root.val)!=from)findAns(parent.get(root.val),root,depth+1,k);
    }
}

96. 不同的二叉搜索树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public int numTrees(int n) {
        //初始化 dp 数组
        int[] dp = new int[n + 1];
        //初始化0个节点和1个节点的情况
        dp[0] = 1;
        dp[1] = 1;
        for (int i = 2; i <= n; i++) {
            for (int j = 1; j <= i; j++) {
                //对于第i个节点，需要考虑1作为根节点直到i作为根节点的情况，所以需要累加
                //一共i个节点，对于根节点j时,左子树的节点个数为j-1，右子树的节点个数为i-j
                dp[i] += dp[j - 1] * dp[i - j];
            }
        }
        return dp[n];
    }
}

513. 找树左下角的值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    //思路：记录深度，更新最新值
    int ret;
    int maxDepth;
    public int findBottomLeftValue(TreeNode root) {
        ret = root.val;
        dfs(root,1);
        return ret;
    }
    public void dfs(TreeNode root,int dpeth){
        if(root==null)return;
        if(dpeth>maxDepth){
            if(root.left!=null){
                ret=root.left.val;
                maxDepth = dpeth;
            }else if(root.right!=null) {
                ret=root.right.val;
                maxDepth = dpeth;
            }
        }
        if(root.left!=null)dfs(root.left,dpeth+1);
        if(root.right!=null)dfs(root.right,dpeth+1);
    }
}

700. 二叉搜索树中的搜索（easy）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    //迭代
    public TreeNode searchBST(TreeNode root, int val) {
        while(root!=null){
            if(root.val==val)return root;
            root = root.val>val ? root.left:root.right;
        }
        return null;
    }
    //递归
    public TreeNode searchBST0(TreeNode root, int val) {
        if(root==null)return null;
        if(root.val==val)return root;
        return root.val>val ? searchBST(root.left,val): searchBST(root.right,val);
    }
}

404. 左叶子之和（easy）

1
2
3
4
5
6
7
8
9
10
11
class Solution {
    //左且叶子节点
    int ret;
    public int sumOfLeftLeaves(TreeNode root) {
        if(root==null)return 0;
        if(root.left!=null&&root.left.left==null&&root.left.right==null)ret+=root.left.val;
        if(root.left!=null)sumOfLeftLeaves(root.left);
        if(root.right!=null)sumOfLeftLeaves(root.right);
        return ret;
    }
}

617. 合并二叉树（easy）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    public TreeNode mergeTrees(TreeNode t1, TreeNode t2) {
        if (t1 == null) return t2;
        if (t2 == null) return t1;
        TreeNode merged = new TreeNode(t1.val + t2.val);
        merged.left = mergeTrees(t1.left, t2.left);
        merged.right = mergeTrees(t1.right, t2.right);
        return merged;
    }
    public TreeNode mergeTrees0(TreeNode root1, TreeNode root2) {
        if(root1==null&&root2==null)return null;
        if(root1==null)root1 = new TreeNode();
        root1.val+=root2==null?0:root2.val;
        if(root1.left==null&&root2!=null&&root2.left!=null)root1.left = new TreeNode();
        if(root1.right==null&&root2!=null&&root2.right!=null)root1.right = new TreeNode();
        if(root2!=null)mergeTrees(root1.left,root2.left);
        if(root2!=null)mergeTrees(root1.right,root2.right);
        return root1;
    }
}

530. 二叉搜索树的最小绝对差

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
    //基于二叉搜索树的性质可知中序遍历后呈递增序列
    //通过pre记录前一个节点的值即可与当前节点计算差值
    int pre;
    int ans;
    public int getMinimumDifference(TreeNode root) {
        ans = Integer.MAX_VALUE;
        pre = -1;
        dfs(root);
        return ans;
    }
    public void dfs(TreeNode root) {
        if (root == null) return;
        dfs(root.left);
        if (pre == -1) {
            pre = root.val;
        } else {
            ans = Math.min(ans, root.val - pre);
            pre = root.val;
        }
        dfs(root.right);
    }
}

173. 二叉搜索树迭代器

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class BSTIterator {
    private int index;
    private List<Integer> data;
    public BSTIterator(TreeNode root) {
        data = new ArrayList<>();
        //中序遍历
        int index = 0;
        Stack<TreeNode> stack = new Stack<>();
        while(root!=null||!stack.isEmpty()){
            while(root!=null){
                stack.push(root);
                root = root.left;
            }
            if(!stack.isEmpty()){
                root = stack.pop();
                data.add(root.val);
                root = root.right;
            }
        }
    }
    public int next() {
        return data.get(index++);
    }
    
    public boolean hasNext() {
        return index<data.size();
    }
}

701. 二叉搜索树中的插入操作

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    //二叉搜索树性质：root.left<root<root.right
    public TreeNode insertIntoBST(TreeNode root, int val) {
        if(root==null)root=new TreeNode(val);
        if (val>root.val){
            if(root.right==null)root.right = new TreeNode(val);
            else insertIntoBST(root.right,val);
        }
        if (val<root.val){
            if (root.left==null)root.left = new TreeNode(val);
            else insertIntoBST(root.left,val);
        }
        return root;
    }
}

剑指 Offer 26. 树的子结构

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
    public boolean isSubStructure(TreeNode A, TreeNode B) {
        if(A==null||B==null)return false;
        if(A.val==B.val && compare(A,B))return true;
        return isSubStructure(A.left,B)|| isSubStructure(A.right,B);
    }
    public boolean compare(TreeNode t1,TreeNode t2){
        if(t1==null&&t2==null)return true;
        if(t1==null&&t2!=null)return false;
        if(t1!=null&&t2==null)return true;
        if(t1.val!=t2.val)return false;
        return compare(t1.left,t2.left) && compare(t1.right,t2.right);
    }
}

二叉树的下一个节点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public class Solution {
    public TreeLinkNode GetNext(TreeLinkNode pNode) {
        //1.空直接返回
        if(pNode==null)return null;
        //2.右子树为空需要分为两种情况
        if(pNode.right==null){
            if(pNode.next==null)return null;
            //1.pNode是父节点的左子树，则返回父节点
            if(pNode.next.left==pNode)return pNode.next;
            //2.pNode是父节点的右子树，则一直往上查找当当前节点是父节点的左子树，返回父节点
            while(pNode.next!=null&&pNode.next.left!=pNode)pNode=pNode.next;
            return pNode.next;
        }
        //3.右子树不为空则查找右子树最左的值
        return dfs(pNode.right);
    }
    public TreeLinkNode dfs(TreeLinkNode pNode) {
        if(pNode.left!=null)return dfs(pNode.left);
        return pNode;
    }
}

1339. 分裂二叉树的最大乘积（mid)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    long sum;
    long best;
    public int maxProduct(TreeNode root) {
        sum(root);
        dfs(root);
        long l = best * (sum - best);
        return (int)(l % 1000000007);
    }
    //分割子树
    private long dfs(TreeNode root) {
        if (root==null)return 0;
        long cur = dfs(root.left)+dfs(root.right)+root.val;
        if(Math.abs(cur*2-sum)<Math.abs(best*2-sum))best=cur;//均值差值越小则乘积越大
        return cur;
    }
    //计算所有节点和
    public void sum(TreeNode root){
        if(root==null)return;
        sum+=root.val;
        sum(root.left);
        sum(root.right);
    }
}

1302. 层数最深叶子节点的和（mid）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    int layer;
    int ret;
    //思路：注意是层数最深的节点，dfs判断层数和累计最深层节点
    public int deepestLeavesSum(TreeNode root) {
        dfs(root,0,0);
        return ret;
    }
    public void dfs(TreeNode root,int lay,int sum){   
        if(lay==layer)ret+=root.val;     
        if(lay>layer){
            layer=lay;
            ret = root.val;
        }
        if(root==null)return;
        if(root.left!=null)dfs(root.left,lay+1,sum+root.val);
        if(root.right!=null)dfs(root.right,lay+1,sum+root.val);
    }
}

589. N 叉树的前序遍历（easy）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
    List<Integer> ret = new ArrayList<>();
    public List<Integer> preorder0(Node root) {
        if(root==null)return ret;
        ret.add(root.val);
        for(Node node:root.children)preorder(node);
        return ret;
    }
    public List<Integer> preorder(Node root) {
        List<Integer> ret = new ArrayList<>();
        if(root==null)return ret;
        Stack<Node> stack = new Stack<>();
        stack.push(root);
        while(!stack.isEmpty()){
            Node node = stack.pop();
            ret.add(node.val);
            for (int i = node.children.size() - 1; i >= 0; --i) {
                stack.push(node.children.get(i));
            }
        }
        return ret;
    }
}

307. 区域和检索 - 数组可修改（mid）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
class NumArray {
    //线段数（叶子节点都是数组的元素）
    //[1,3,5]       [1,3,5,7]        ......
    //      9           16
    //     / \         /  \
    //    4   5       4    12
    //   / \         / \   / \
    //  1   3       1   3 5   7      ......
    // n=3 node=6   n=4 node=7     n=5 node=9  n=6 node=12  node<=2*n
    int[] tree;
    int n;
    public NumArray(int[] nums) {
        n = nums.length;
        tree = new int[2*n];
        buildTree(nums);
    }
    //构建线段树
    public void buildTree(int[] nums){
        //nums=[1,3,5,7] tree = [0,0,0,0,1,3,5,7] 
        //将所有叶子节点放置在[n,2n)数组中
        for (int i = n, j = 0;  i < 2 * n; i++,  j++)tree[i] = nums[j];
        //tree = [0,16,4,12,1,3,5,7] 
        //把父节点放置在[1,n)数组中 , tree[i] = tree[i * 2] + tree[i * 2 + 1]
        for (int i = n - 1; i > 0; --i)tree[i] = tree[i * 2] + tree[i * 2 + 1];
    }
    //更新某个下标同时需要更新其父节点的值
    public void update(int index, int val) {
        index+=n;//下标的位置,n+下标
        tree[index] = val;
        //更新父亲节点,因为tree[i] = tree[i * 2] + tree[i * 2 + 1];所以index如果是奇数则为右子树，index是偶数则为左子树
        while(index>0){
            int left = index;
            int right = index;
            if(index % 2 == 0) right = index+1;
            else left = index - 1;
            //更新父节点值
            tree[index / 2] = tree[left] + tree[right];
            //更新下标
            index /= 2;
        }

    }
    //求和只需要获取其父节点
    public int sumRange(int left, int right) {
        //确认在数组中的下标
        left+=n;
        right+=n;
        int ret = 0;
        //[1,3,5,7]
        while(left<=right){
            //1.如果left是左子树可以直接取根节点,如果是右子树那只取右节点
            if(left % 2 == 1 ){
                ret+=tree[left];
                left++;
            }
            //2.如果right是右子树可以直接取根节点,如果是左子树那只取左节点
            if(right % 2 == 0 ){
                ret+=tree[right];
                right--;
            }
            left/=2;
            right/=2;
        }
        return ret;
    }
}

951. 翻转等价二叉树（mid）

1
2
3
4
5
6
7
8
class Solution {
    //递归交互左右子树判断
    public boolean flipEquiv(TreeNode root1, TreeNode root2) {
        if (root1 == root2)return true;
        if (root1 == null || root2 == null || root1.val != root2.val)return false;
        return (flipEquiv(root1.left, root2.left) && flipEquiv(root1.right, root2.right) || flipEquiv(root1.left, root2.right) && flipEquiv(root1.right, root2.left));
    }
}

538. 把二叉搜索树转换为累加树（mid）

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
    //中序遍历:右-根-左
    int sum;
    public TreeNode convertBST(TreeNode root) {
        if(root==null)return root;
        if(root.right!=null)convertBST(root.right);
        sum+=root.val;
        root.val = sum;
        if(root.left!=null)convertBST(root.left);
        return root;
    }
}

814. 二叉树剪枝（mid）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    //dfs
    public TreeNode pruneTree(TreeNode root) {
        dfs(root);
        return root!=null&&root.left==null&&root.right==null&&root.val==0?null:root;
    }
    public boolean dfs(TreeNode root){
        if(root==null)return true;
        boolean left = true,right = true;
        if(root.left!=null)left = dfs(root.left);
        if(root.right!=null)right = dfs(root.right);
        //左右节点都是0才能移除
        if(left)root.left = null;
        if(right)root.right = null;
        return left && right && root.val==0;
    }
}

669. 修剪二叉搜索树（mid）

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
    //思路：基于二叉搜索树，其左子树都小于根节点，右子树都大于根节点
    public TreeNode trimBST(TreeNode root, int L, int R) {
        if (root == null) return root;
        if (root.val > R) return trimBST(root.left, L, R);//去除右子树
        if (root.val < L) return trimBST(root.right, L, R);//去除左子树
        //如果root.val在区[L,R]区间,则递归判断其左右子树
        root.left = trimBST(root.left, L, R);
        root.right = trimBST(root.right, L, R);
        return root;
    }
}

1325. 删除给定值的叶子节点（mid）

1
2
3
4
5
6
7
8
9
10
11
class Solution {
    //思路：自底向上删除
    public TreeNode removeLeafNodes(TreeNode root, int target) {
        if(root==null)return root;
        if(root.left!=null)removeLeafNodes(root.left,target);
        if(root.right!=null)removeLeafNodes(root.right,target);
        if(root.left!=null&&root.left.val==target&&root.left.left==null&&root.left.right==null)root.left=null;
        if(root.right!=null&&root.right.val==target&&root.right.left==null&&root.right.right==null)root.right=null;
        return root.left==null&&root.right==null&&root.val==target?null:root;
    }
}

1026. 节点与其祖先之间的最大差值（mid）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    int ret;
    public int maxAncestorDiff(TreeNode root) {
        dfs(root,0,100000);
        return ret;
    }
    public void dfs(TreeNode root,int max,int min){
        if(root==null)return;
        max=Math.max(max,root.val);
        min=Math.min(min,root.val);
        ret=Math.max(ret,max-min);
        if(root.left!=null)dfs(root.left,max,min);
        if(root.right!=null)dfs(root.right,max,min);
    }
}

687. 最长同值路径（mid)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    //思路:dfs遍历每次返回左右子树最大的值，ret取的是max(左右子树路径,左右子树路径最大值+根)
    int ret = 0;
    public int longestUnivaluePath(TreeNode root) {
        if(root==null)return 0;
        dfs(root,root.val);
        if(root.left!=null)longestUnivaluePath(root.left);
        if(root.right!=null)longestUnivaluePath(root.right);
        return ret;
    }
    public int dfs(TreeNode root,int target){
        if(root==null||root.val!=target)return 0;
        int l = dfs(root.left,target);
        int r = dfs(root.right,target);
        int c = Math.max(l,r)+1;
        ret=Math.max(Math.max(l+r,c-1),ret);
        return c;
    }
}

979. 在二叉树中分配硬币（mid）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    /**
     * 从后序遍历的第一个叶子节点开始，假设自己有x个金币，剩余x-1个金币都还给父节点，x-1可能为负数、0、正数
     * x-1 < 0说明不够金币，需要从父节点获得，因此子节点有|x-1|个入方向的操作，次数加上|x-1|
     * x-1 == 0说明刚好，无需与父节点有金币的交换，次数加0
     * x-1 > 0 说明有多余的金币，需要交给父节点，因此子节点有x-1个出方向的操作，次数加上|x-1|
     */
    private int ans = 0;// 移动次数
    public int distributeCoins(TreeNode root) {
        lrd(root);
        return ans;
    }
    public int lrd(TreeNode root){
        if(root == null) return 0;
        if(root.left != null){
            root.val += lrd(root.left);
        }
        if(root.right != null){
            root.val += lrd(root.right);
        }
        ans += Math.abs(root.val - 1);
        return root.val - 1;
    }
}

715. Range 模块（hard）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
class RangeModule {
        private TreeMap<Integer,Integer> map;
        public RangeModule() {
            this.map = new TreeMap<>();
        }
        public void addRange(int left, int right) {
            int actualLeft = left,actualRight = right;
            //1.向左边检查是否有可以覆盖的
            Integer leftFloorKey = map.floorKey(left);
            //如果有个区间已经包含当前需要新增的区间则无需改动
            if (leftFloorKey!=null &&leftFloorKey<=left&↦.get(leftFloorKey)>=right)return;
            while (leftFloorKey!= null && map.get(leftFloorKey)>=left){
                actualLeft = leftFloorKey;
                map.remove(leftFloorKey);
                leftFloorKey = map.floorKey(leftFloorKey);
            }
            //2.向右边检查是否有可以覆盖的
            Integer leftCeilKey = map.ceilingKey(left);
            while (leftCeilKey!= null && map.get(leftCeilKey)<=right){
                map.remove(leftCeilKey);
                leftCeilKey = map.ceilingKey(leftCeilKey);
            }
            //3.确定最终right
            if (leftCeilKey!= null && leftCeilKey<=right){
                actualRight = map.get(leftCeilKey);
                map.remove(leftCeilKey);
            }
            //确保[actualLeft,actualRight]没有值
            Integer remove = map.ceilingKey(actualLeft);
            while (remove!=null&↦.get(remove)<actualRight){
                map.remove(remove);
                remove = map.ceilingKey(actualLeft);
            }
            map.put(actualLeft,actualRight);
        }

        public boolean queryRange(int left, int right) {
            Integer floorKey = map.floorKey(left);
            if (floorKey==null&↦.get(left)==null)return false;
            Integer floorValue = map.get(floorKey);
            if (floorValue>=right)return true;
            return false;
        }

        public void removeRange(int left, int right) {
            //左边区间去掉相交部分
            Integer floorKey = map.floorKey(left);
            if (floorKey!=null){
                Integer floorValue = map.get(floorKey);
                if (floorValue>left)map.put(floorKey,left);
                if (floorValue>right)map.put(right,floorValue);
            }
            //中间区间全部去除
            Integer leftCeilKey = map.ceilingKey(left);
            while (leftCeilKey!= null && leftCeilKey<right){
                Integer leftCeilValue = map.get(leftCeilKey);
                if (leftCeilValue>right){
                    map.put(right,leftCeilValue);
                }
                map.remove(leftCeilKey);
                leftCeilKey = map.ceilingKey(leftCeilKey);
            }
        }
    }

834. 树中距离之和（hard）

1

相关资料

基础算法 > 刷题记录
算法笔记-二叉树/线段树/排序树
https://mikeygithub.github.io/2021/12/29/yuque/算法笔记-二叉树!线段树!排序树/
作者
Mikey
发布于
2021年12月29日
许可协议