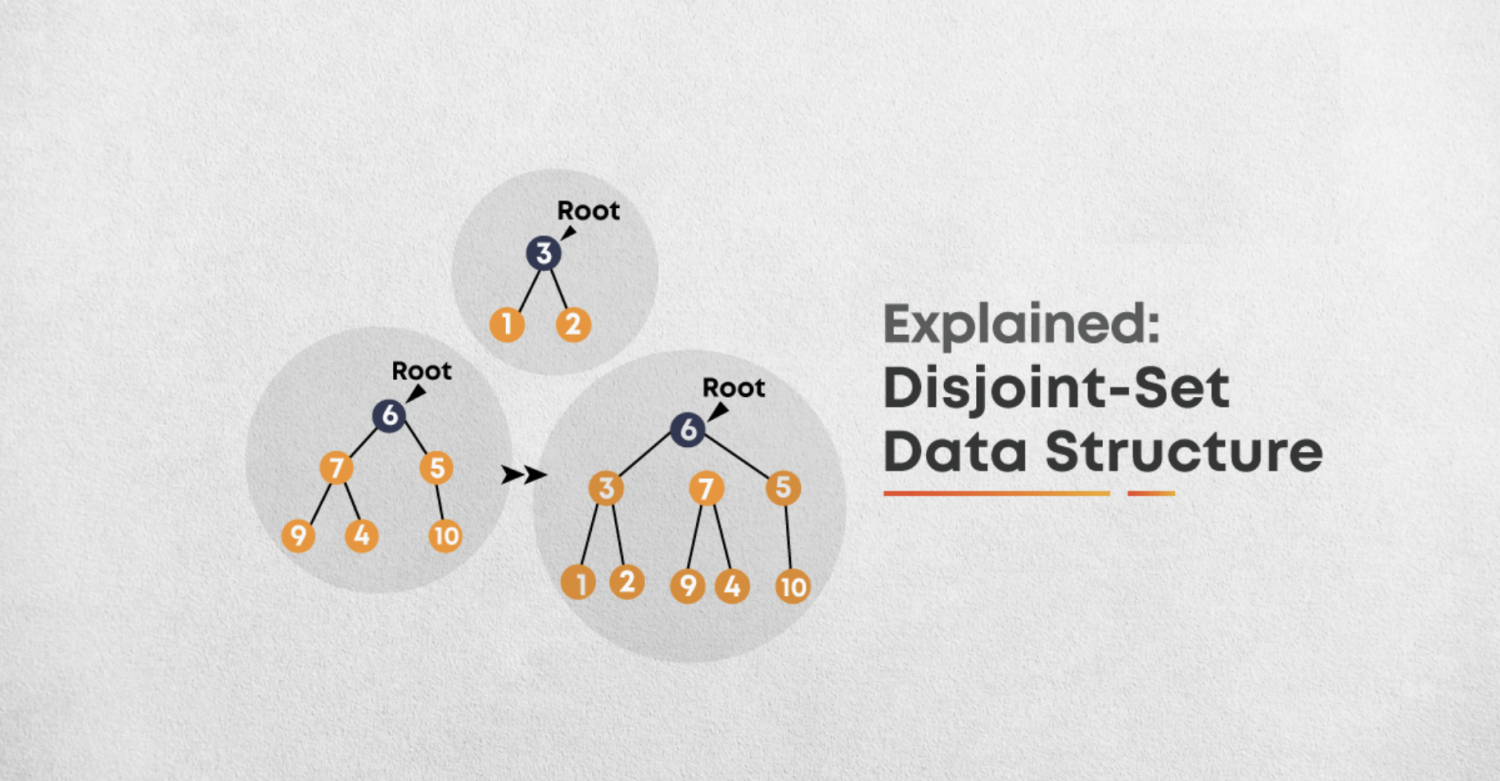
背景
在一些有N个元素的集合应用问题中,我们通常是在开始时让每个元素构成一个单元素的集合,然后按一定顺序将属于同一组的元素所在的集合合并,其间要反复查找一个元素在哪个集合中。这一类问题其特点是看似并不复杂,但数据量极大,若用正常的数据结构来描述的话,往往空间上过大,计算机无法承受;即使在空间上勉强通过,时间复杂度也极高。
简介
并查集(Disjoint Sets )是一种属性结构(通过数组存储),主要用于处理多个集合求交集问题。集就是让每个元素构成一个单元素的集合,也就是按一定顺序将属于同一组的元素所在的集合合并。主要是通过集合数组+元素数组来进行存储。
支持的两种操作
- 查找(Find):确定某个元素处于哪个子集;
- 合并(Union):将两个子集合并成一个集合。
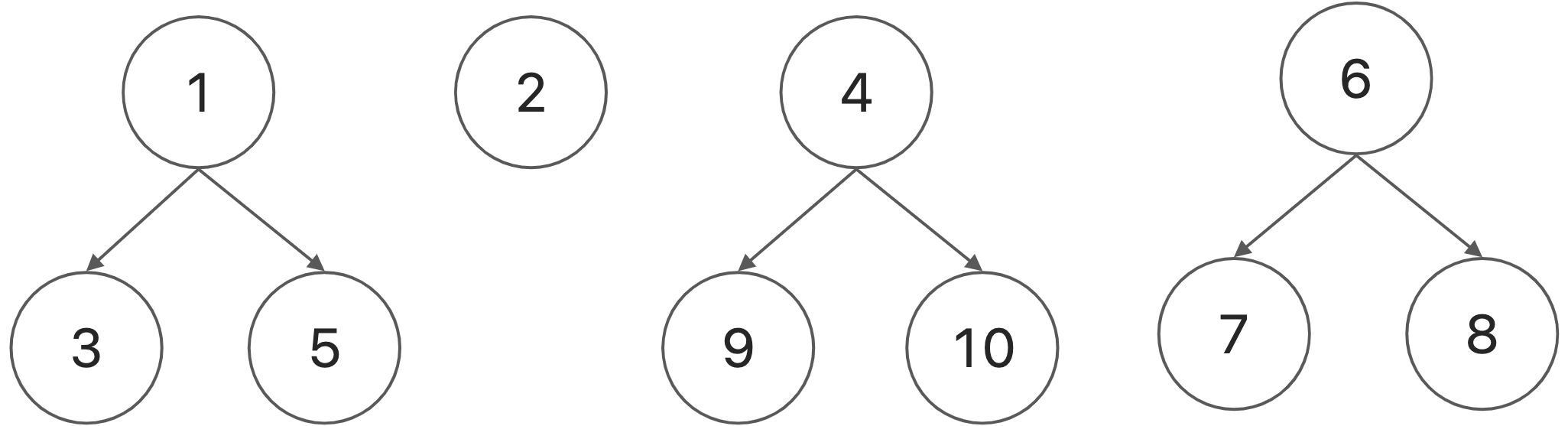
用编号最小的元素标记所在集合;定义一个数组 set[1..n] ,其中set[i] 表示元素i 所在的集合
$ 集合 = {1,3,5},{2},{4,9,10},{6,7,8} $
| rank |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| parent |
1 |
2 |
1 |
4 |
1 |
6 |
6 |
6 |
4 |
4 |
实现
**数组**:一个整数数组,称为parent[]。如果我们处理n个项目,数组的第i个元素代表第i个项目。更准确地说,数组的第i个元素是第i个项的父元素。这些关系创建一个或多个虚拟树。
**树**:这是一个不相交的集合。如果两个元素位于同一棵树中,则它们位于同一集合中。每个树的根节点(或最上面的节点)称为集合的代表。每一组都有一个独特的代表。识别代表的一个简单规则是,如果我是一个集合的代表,那么parent[i]=i。如果我不是他的集合的代表,那么可以沿着树向上移动,直到找到代表。
初始化
建立两个数组分别为rank,parent初始化其长度
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| public class DisjointUnionSets {
int[] rank;
int[] parent;
int n;
public DisjointUnionSets(int n) {
rank = new int[n];
parent = new int[n];
this.n = n;
makeSet();
}
void makeSet() {
for (int i = 0; i < n; i++) {
parent[i] = i;
}
}
}
|
查找
可以通过递归地遍历父数组来实现,直到我们到达一个节点,该节点是其自身的父节点。
1
2
3
4
5
6
7
8
9
| public int find(int i) {
if (parent[i] == i) {
return i;
} else {
return find(parent[i]);
}
}
|
合并
需要两个元素作为输入。并使用find操作查找其集合的代表,最后将其中一棵树(代表集合)放在另一棵树的根节点下,从而有效地合并树和集合。
1
2
3
4
5
6
7
8
9
|
void union(int i, int j) {
int irep = this.Find(i);
int jrep = this.Find(j);
this.Parent[irep] = jrep;
}
|
完整实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
| package io.example.algorithm.disjointset;
public class DisjointUnionSets {
int[] rank;
int[] parent;
int n;
public DisjointUnionSets(int n) {
rank = new int[n];
parent = new int[n];
this.n = n;
makeSet();
}
void makeSet() {
for (int i = 0; i < n; i++) {
parent[i] = i;
}
}
int find(int x) {
if (parent[x] != x) {
parent[x] = find(parent[x]);
}
return parent[x];
}
void union(int x, int y) {
int xRoot = find(x), yRoot = find(y);
if (xRoot == yRoot) return;
if (rank[xRoot] < rank[yRoot])
parent[xRoot] = yRoot;
else if (rank[yRoot] < rank[xRoot])
parent[yRoot] = xRoot;
else
{
parent[yRoot] = xRoot;
rank[xRoot] = rank[xRoot] + 1;
}
}
public static void main(String[] args) {
int n = 5;
DisjointUnionSets dus = new DisjointUnionSets(n);
dus.union(0, 2);
dus.union(4, 2);
dus.union(3, 1);
if (dus.find(4) == dus.find(0)) System.out.println("Yes");
else System.out.println("No");
if (dus.find(1) == dus.find(0)) System.out.println("Yes");
else System.out.println("No");
}
}
|
案例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
| class Solution {
class UnionFind {
int count;
int[] parent;
int[] rank;
public UnionFind(char[][] grid) {
count = 0;
int m = grid.length;
int n = grid[0].length;
parent = new int[m * n];
rank = new int[m * n];
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (grid[i][j] == '1') {
parent[i * n + j] = i * n + j;
++count;
}
rank[i * n + j] = 0;
}
}
}
public int find(int i) {
if (parent[i] != i) parent[i] = find(parent[i]);
return parent[i];
}
public void union(int x, int y) {
int rootx = find(x);
int rooty = find(y);
if (rootx != rooty) {
if (rank[rootx] > rank[rooty]) {
parent[rooty] = rootx;
} else if (rank[rootx] < rank[rooty]) {
parent[rootx] = rooty;
} else {
parent[rooty] = rootx;
rank[rootx] += 1;
}
--count;
}
}
public int getCount() {
return count;
}
}
public int numIslands(char[][] grid) {
if (grid == null || grid.length == 0) {
return 0;
}
int nr = grid.length;
int nc = grid[0].length;
int num_islands = 0;
UnionFind uf = new UnionFind(grid);
for (int r = 0; r < nr; ++r) {
for (int c = 0; c < nc; ++c) {
if (grid[r][c] == '1') {
grid[r][c] = '0';
if (r - 1 >= 0 && grid[r-1][c] == '1') {
uf.union(r * nc + c, (r-1) * nc + c);
}
if (r + 1 < nr && grid[r+1][c] == '1') {
uf.union(r * nc + c, (r+1) * nc + c);
}
if (c - 1 >= 0 && grid[r][c-1] == '1') {
uf.union(r * nc + c, r * nc + c - 1);
}
if (c + 1 < nc && grid[r][c+1] == '1') {
uf.union(r * nc + c, r * nc + c + 1);
}
}
}
}
return uf.getCount();
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
| class Solution {
int[] parent;
public long countPairs(int n, int[][] edges) {
parent = new int[n];
for (int i = 0; i < n; i++) {
parent[i] = i;
}
for(int[] edge:edges){
union(edge[0],edge[1]);
}
Map<Integer,Integer> map = new HashMap<>();
for (int i = 0; i < n; i++) {
int root = find(i);
map.put(root,map.getOrDefault(root,0)+1);
}
long ret = 0;
for(int key:map.keySet()){
int cnt = map.get(key);
ret +=(long)cnt * (n-cnt);
}
return ret >> 1;
}
public int find(int i) {
if (parent[i] == i) {
return i;
} else {
return find(parent[i]);
}
}
public void union(int i, int j) {
int irep = this.find(i);
int jrep = this.find(j);
this.parent[jrep] = irep;
}
}
|
资料
https://www.geeksforgeeks.org/disjoint-set-data-structures/?ref=gcse


