数据结构篇-B树B+树B*树

BST
二叉搜索树,左节点小于根节点、右节点大于根节点,其子节点也遵循这个规则
B-Tree
B树又称为多路平衡查找树,是一种组织和维护外存文件系统非常有效的数据结构。
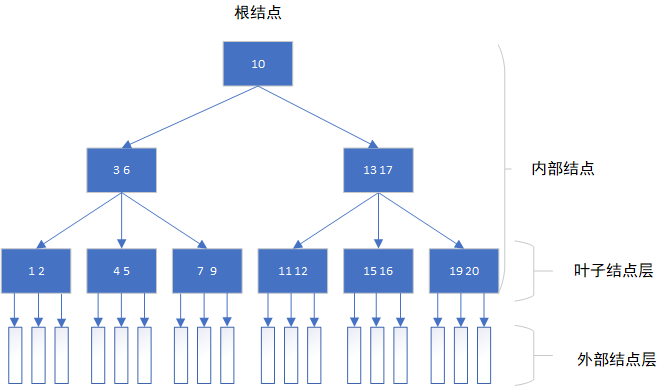
一棵m阶B树或者是一棵空树,或者是满足要求的m叉树:
1.树中每个结点至多有m个孩子结点(即至多有m-1个关键字);
最多关键字个数Max=m-1
2.除根结点外,其他非叶子节子点至少有[m/2]个孩子结点(即至少有[m/2]-1=[(m-1)/2]个关键字)
最少关键字个数Min=[m/2]-1
3.若根结点不是叶子结点,则根结点至少有两个孩子结点;
4.每个结点的结构如下,结点中按关键字大小顺序排列:n p0 k1 p1 k2 p2 … kn pn
5.所有外部结点都在同一层上。B树是所有结点的平衡因子均等于0的多路查找树。在计算B树的高度时,需要计入最底层的外部结点
6.外部结点就是失败结点,指向它的指针为空,不含有任何信息,是虚设的。一棵B树中总有n个关键字,则外部结点个数为n+1。
代码结构
1 | |
查找
将k与根结点中的key[i]进行比较:
1.若k=key[i],则查找成功;
2.若k<key[1],则沿着指针ptr[0]所指的子树继续查找;
3.若key[i]<k<key[i+1],则沿着指针ptr[i]所指的子树继续查找;
4.若k>key[n],则沿着指针ptr[n]所指的子树继续查找。
说明:当查找到某个叶结点时,若相应的指针为空,落入一个外部结点,表示查找失败。
插入
插入流程
1.查找该关键字的插入结点(注意B树的插入结点一定是叶子结点层的结点)。
2.插入关键字。
1.插入结点有空位置,即关键字个数n<m-1:直接把关键字k有序插入到该结点的合适位置上。
2.插入结点没有空位置,即原关键字个数n=m-1 -> 分裂。
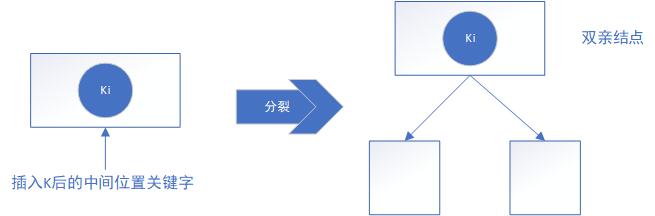
如果没有双亲结点,新建一个双亲结点,树的高度增加一层。
如果有双亲结点,将ki插入到双亲结点中。
例子 关键字序列为:(1,2,6,7,11,4,8,13,10,5,17,9,16,20,3,12,14,18,19,15)。创建一棵5阶B树。
注意:最多的关键字个数 Max = m-1 = 4

删除
删除过程
(1)查找关键字k所在的结点。
(2)删除关键字k。
删除关键字k分两种情况:
- 在叶子结点层上删除关键字k。
- 在非叶子结点层上删除关键字k。
注意:非根、非叶子结点的关键字最少个数Min=m/2-1
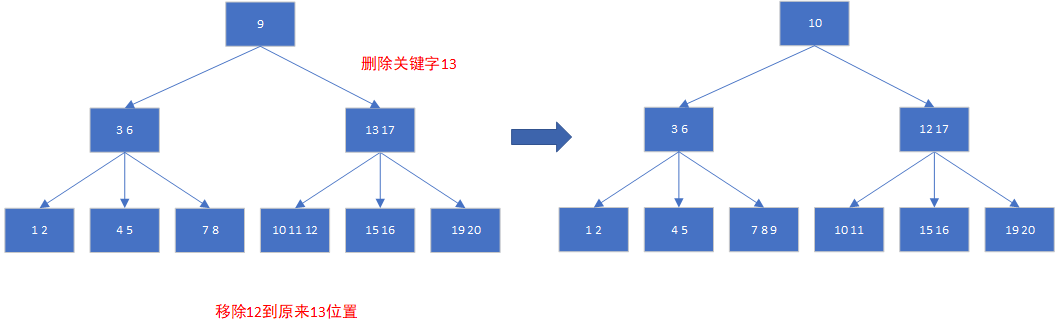
在B树的叶子结点b上删除关键字共有以下3种情况:
- 假如b结点的关键字个数大于Min,说明删去该关键字后该结点仍满足B树的定义,则可直接删去该关键字。

- 假如b结点的关键字个数等于Min,说明删去关键字后该结点将不满足B树的定义。若可以从兄弟结点借。

- 假如b结点的关键字个数等于Min,说明删去关键字后该结点将不满足B树的定义。若不能从兄弟结点借。
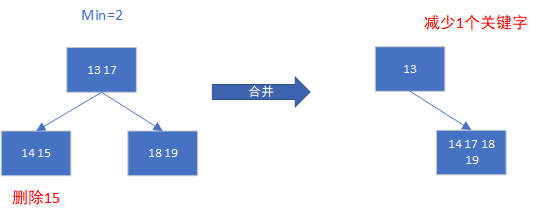
对于前例生成的B树,给出删除8,16,15,4等4个关键字的过程。

B+Tree
B+树是B树的一些变形。一棵4阶的B+树示例:
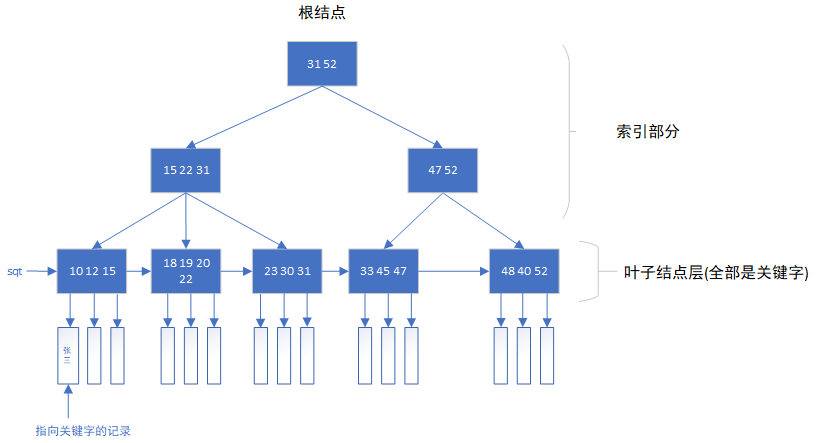
B+树的定义 一棵m阶B+树满足下列要求:
每个分支结点至多有m棵子树(这里m=4)。
根结点或者没有子树,或者至少有两棵子树。
除根结点外,其他每个分支结点至少有 m/2 棵子树。
有n棵子树的结点恰好有n个关键字
所有叶子结点包含全部关键字及指向相应记录的指针,而且叶子结点按关键字大小顺序链接。并将所有叶子结点链接起来。
所有分支结点(可看成是索引的索引)中仅包含它的各个子结点(即下级索引的索引块)中最大关键字及指向子结点的指针。
m阶的B+树和m阶的B树的主要的差异 :
- (1)有n棵子树的结点中含有n个关键码;
- (2)所有的叶子结点中包含了全部关键码的信息,及指向含有这些关键码记录的指针,且叶子结点本身依关键码的大小自小而大的顺序链接;
- (3)所有的非终端结点可以看成是索引部分,结点中仅含有其子树根结点中最大(或最小)关键码。
注意:MySQL中的索引部分是B+Tree的,但是和上面的还是有一定的区别,其索引在Tree的同级还有指向前后节点的指针,且叶子节点之间是双向链表。
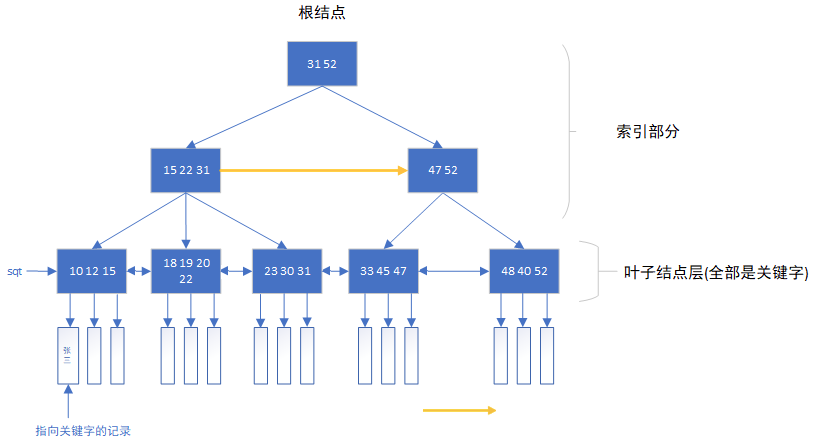
1 | |
B*Tree
B*Tree同样是BTree的变体
m阶B*-树是一个搜索树,它要么为空,要么满足三个属性:
- 根节点具有最小两层和最大两层((2m-2)/3)+1个子节点
- 其他内部节点具有最小层((2m-1)/3)和最大m个子节点
- 所有外部节点位于同一级别。
