刷题笔记-位运算/进制转换

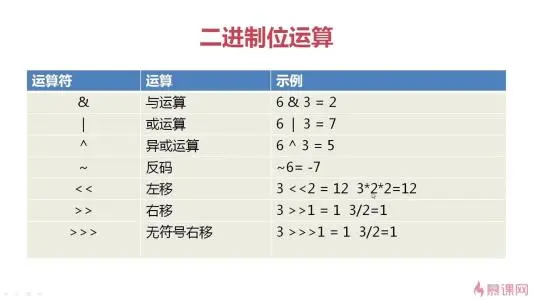
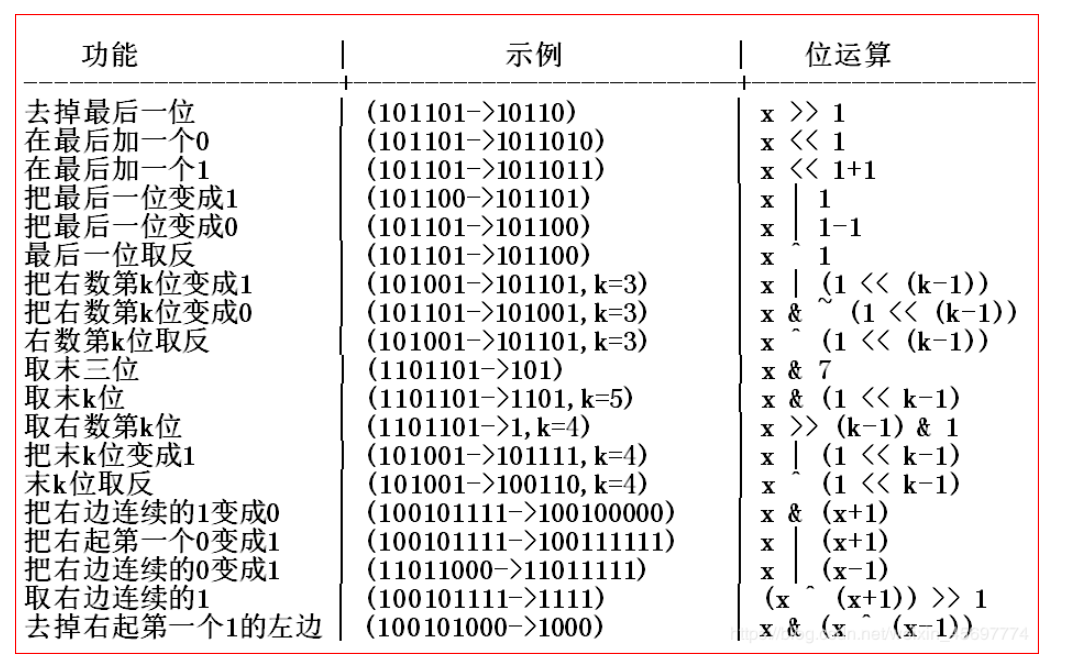
位移运算

功能 示例 位运算
判断n是否为2的幂次方 1101 0101 & 1101 0100 = n > 0 && (n & (n - 1)) == 0;
n > 0 && (n & -n) == n;

进制转换

十进制转 x 进制

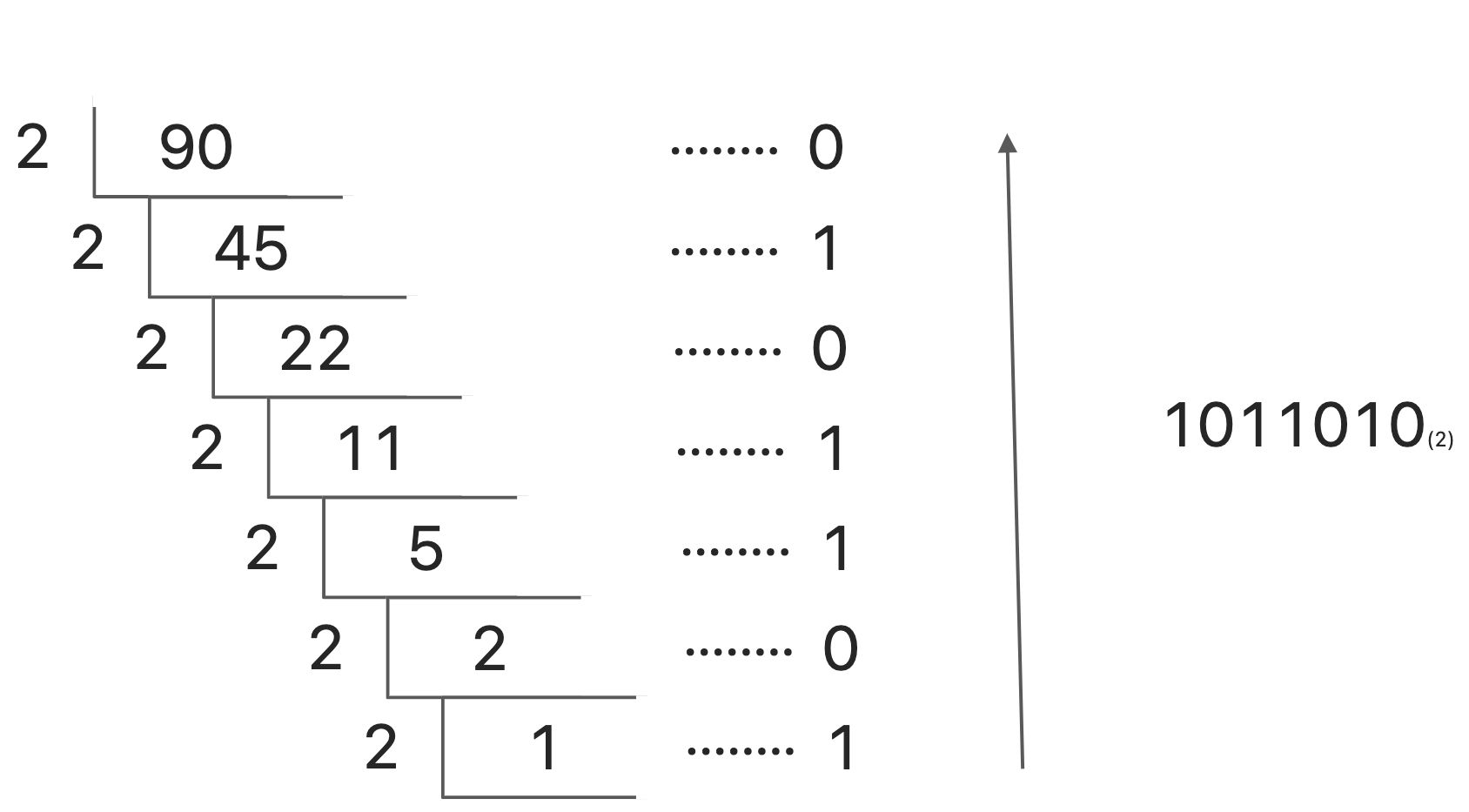
  • 短除法：用十进制的数除以 x 取余，最后从下往上去余数

画板

1

x进制转十进制

  • 要从右到左用二进制的每个数去乘以 x 的相应次方

$ x进制转为十进制公式=abcd.efg_{(x)}=d20+c21+b22+a23+e2-1+f2-2+g*2-3_{（10）} $

  • 案例

$ Bin = 1011010_{(2)} =
Dec = 2^0 *0 + 2^1 * 1+ 2^2 * 0 + 2^3 * 1+ 2^4 * 1 + 2^5 * 0 + 2^6 * 1 = 0 + 2 +0+ 8 + 16+0+64=90_{(10)} $

1

3.十进制转为负 x 进制

  • 遇到了负进制数，我们取余的时候余数会出现负的情况，我们就要处理这个负数的情况。我们可以经过以下的变换：

$ N/R=B…..X: N是被除数，R是除数（R为负数），B是商，X是余数。\
BR+X=N \
BR+X-R+R=N\
（B+1）* R + X-R=N\
（B+1）* R +（X-R）=N\
（B+1）是商 ，（X-R）是余 $

经过这样的变换之后那么X-R就是正数了。那么我们也可以得到一个结论：**当余数为负数时，余数=余数-除数（除数为负数），商=商+1**。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    //十进制转负二进制
    //A/B=C余D
    //C*B+D=A
    //C*B+D+B-B=A
    //C*B+D+B-B=A
    //C*B-B+D+B=A
    //(C+1)*B+(D-B)=A (B为负数,当D为负数,所以D-B必定为正数)
    public String baseNeg2(int n) {
        StringBuilder sb = new StringBuilder();
        if(n==0)return "0";
        while(n!=0){
            int mod = n % -2;
            n = n / -2;
            if(mod<0){
                mod = mod + 2;
                n++;
            }
            sb.append(mod);
        }
        sb.reverse();
        return sb.toString();
    }
}

小数点转二进制

案例：192.324（十进制）转为二进制

  1. 整数部分192（十进制）= 11000000（二进制）
  2. 小数部分0.324（十进制）= 0.324 * 2 = 0.648 = 整数部分 = 0

= 0.648 * 2 = 1.296 = 整数部分 = 1

= 0.296 * 2 = 0.592 = 整数部分 = 0

= 0.592 * 2 = 1.184 = 整数部分 = 1

= 0.184 * 2 = 0.368 = 整数部分 = 0

= 0.184 * 2 = 0.368 = 整数部分 = 0

………直到*2=不带小数，从上到下取二进制即为小数部分

= 0101001011110001

不断取乘以2后的整数部分

二进制转小数

11000000.0101001011110001

  1. 整数部分 11000000（二进制）= 12^7 + 12^6 + …… + 1*2^0 = 64 + 128 = 192（十进制）

小数部分 0101001011110001（二进制）= 02^(-1) + 12^(-2) + 02^(-3) + 12^(-4) + 02^(-5) + 02^(-6) + …… + 1 * 2^(-16) = 192.32373046875

从左到右除以2^(n) n=[1,长度]

相关题目

位1的个数(简单)

位移

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution{
    //00000000000000000000000000001011
    //11111111111111111111111111111111
    //&
    //00000000000000000000000000001011
    public int hammingWeight0(int n) {
        int ret = 0;
        int mask = 1;
        for(int i=0;i<32;i++){
            if((n&mask)!=0)ret++;//不等于0就是存在1
            mask<<=1;//左移mask最后一位变为0,所以计算前面一位
        }
        return ret;
    }
    //优化
    //不断把数字最后一个 1 反转，并把答案加一
    //在二进制表示中，数字 n 中最低位的 11 总是对应 n - 1 中的 0。
    //因此，将 n 和 n - 1 与运算总是能把 n 中最低位的 1 变成 0 ，并保持其他位不变。
    //例如：
    //00000000000000000000000000001011 
    //&
    //00000000000000000000000000001010
    //=
    //00000000000000000000000000001010
    public int hammingWeight(int n) {
        int sum = 0;
        while (n != 0) {
            n &= (n - 1);
            sum++;
        }
        return sum;
    }
}

2的幂(简单)

(x & (-x)) == x
(x & (x - 1)) == 0

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
  //位运算：获取二进制中最右边的 1
  //若 x 为 2 的幂，则它的二进制表示中只包含一个 1，则有 x & (-x) = x
  public boolean isPowerOfTwo(int n) {
    if (n == 0) return false;
    long x = (long) n;
    return (x & (-x)) == x;
  }
  //位运算：去除二进制中最右边的 1
  //(x - 1) 代表了将 x 最右边的 1 设置为 0，并且将较低位设置为 1。
  //2 的幂二进制表示只含有一个 1。
  // x & (x - 1) 操作会将 2 的幂设置为 0，因此判断是否为 2 的幂是：判断 x & (x - 1) == 0
  public boolean isPowerOfTwo(int n) {
    if (n == 0) return false;
    long x = (long) n;
    return (x & (x - 1)) == 0;
  }
}

颠倒二进制位(简单)

1011 & 0001 = 0001 获取末尾二进制值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public class Solution {
    public int reverseBits(int n) {
        int result = 0;
        for (int i = 0; i < 32; i++) {
            result <<= 1;
            result += 1 & n;
            n >>= 1;
        }
        return result;
    }
    //优化
    //由于1 & n的值为 0 或者 1，所以返回结果 result 直接加上（1 & n）以更新最后一位数值。
    //这里也可以使用或运算。参与或运算的两个元素，只要有一个为1，那么结果就为1，否则为0。
    public int reverseBits(int n) {
        int result = 0;
        for (int i = 0; i < 32; i++) {
            result <<= 1;//左移一位进行进位
            result |= n & 1;//
            n >>= 1;//n右移一位
        }
        return result;
    }
}

比特位计数(中等)

给定一个非负整数 num。对于 0 ≤ i ≤ num 范围中的每个数字 i ，计算其二进制数中的 1 的数目并将它们作为数组返回。

x>>1右移1位(除以2)，x&1取末位

P(x)=P(x&(x−1))+1;

1
2
3
4
5
6
7
8
public class Solution {
  public int[] countBits(int num) {
      int[] ans = new int[num + 1];
      for (int i = 1; i <= num; ++i)
        ans[i] = ans[i >> 1] + (i & 1); // x / 2 is x >> 1 and x % 2 is x & 1
      return ans;
  }
}

只出现一次的数字(简单)

解题思路

数组列表进行异或即可得出只出现一次的数字

a b a⊕b
0 0 0
0 1 1
1 0 1
1 1 0 
1
2
3
4
5
6
7
8
9
10
class Solution {
    public int singleNumber(int[] nums) {
        int ans = 0;
        for(int i=0;i<nums.length;i++){
            ans = ans^nums[i];
            System.out.println(ans);
        }
        return ans;
    }
}

只出现一次的数字 II(中等)

解题思路

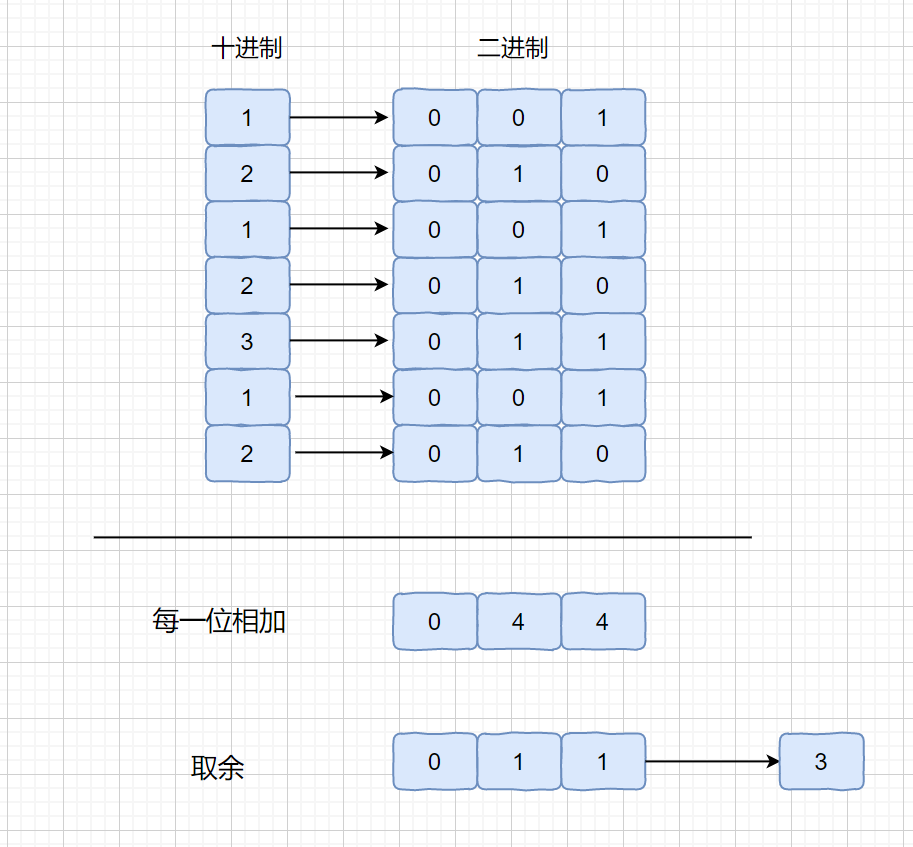
将我们的数的二进制位每一位相加，然后对其每一位的和取余

如果输入是：nums = [2,2,3,2]，那么它的各个元素对应的32位二进制数就是

1
2
3
4
5
6
[
    0000 0000 0000 0000 0000 0000 0000 0010, 
    0000 0000 0000 0000 0000 0000 0000 0010, 
    0000 0000 0000 0000 0000 0000 0000 0011, 
    0000 0000 0000 0000 0000 0000 0000 0010
]

接着，对这些二进制数的对应位进行求和，得到： [00000000000000000000000000000041]；
对这个求和结果的每一位进行3的取模运算，得到：[00000000000000000000000000000011]；
把上面的结果从二进制转换为十进制，就是：3。这就是我们的答案。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public int singleNumber(int[] nums) {
      int res = 0;
      //当前数组为整数32位
      for(int i = 0; i < 32; i++){
          int count = 0;
          for (int j = 0; j < nums.length; j++) {
              //先将数右移，并求出最后一位为 1 的个数
              // 提取从右往左数第i位的数值，将所有nums[i]二进制下的第i位数值进行求和
              if ((nums[j] >> i & 1) == 1) {
                  count++;
              }             
          }
          //找到某一位取余为 1 的数，并左移，为了将这一位循环结束后移至原位
          if (count % 3 != 0) {// 如果没办法被3整除，那么说明落单的那个数的第i位是1不是0
              res = res | 1 << i;
          }
      }
      return res;       
    }
}

只出现一次的数字 III（mid)

解题思路

有两个数只出现了一次记为 num1、num2 初始化为 0, 其余的数出现了两次,我们可以对所有的数进行一次异或操作, 易知这个结果就等于 num1 和 num2 的异或结果(相同的数异或结果都为 0, 0和任意数异或结果都为那个数).

那么我们可以考虑**异或结果的某个非 0 位如最后一个非 0 位, 因为我们知道只有当 num1、num2 在该位不一样的时候才会出现异或结果为 1**. 所以我们以该位是否为 1 对数组进行划分, 只要该位为 1 就和 num1 异或, 只要该位为 0就和 num2 异或, 这样最终得到就是只出现过一次的两个数(其他在该位为 1 或 0 的数必然出现 0/2 次对异或结果无影响)

例： **a,b,a,b,c,d,e,f,e,f ** 分组后
A组：a, a , b, b, c 异或得到 c
B组：e, e, f, f, d 异或得到 d

那么我们应该怎么借助分组位进行分组呢？

我们处理 c , d 的异或值，可以仅保留异或值的分组位，其余位变为 0 ，例如 101 变成 001或 100
为什么要这么做呢？

在第二题提到，我们可以根据 a & 1 来判断 a 的最后一位为 0 还是为 1，所以我们将 101 变成 001 之后，然后数组内的元素 x & 001 即可对 x 进行分组 。同样也可以 x & 100 进行分组.
那么我们如何才能仅保留分组位，其余位变为 0 呢？例 101 变为 001 ，我们可以利用 x & (-x) 来保留最右边的 1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
    public int[] singleNumber(int[] nums) {
        int xorsum = 0;
        //结果就只剩下x1和x2的异或
        for (int num : nums) {
            xorsum ^= num;
        }
        //xorsum & (-xorsum)得出x1,x2最低位非0的数字(最右边为一的位置)
        //防止溢出
        int lsb = (xorsum == Integer.MIN_VALUE ? xorsum : xorsum & (-xorsum));
        int type1 = 0, type2 = 0;
        //将两个不同的数分别放在两个组，这样子各自组进行异或即可得出这两个数
        for (int num : nums) {
            //分为两组
            if ((num & lsb) != 0) {//如果最右边位
                type1 ^= num;
            } else {
                type2 ^= num;
            }
        }
        return new int[]{type1, type2};
    }
}

丢失的数字（easy）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    //思路：排序
    //[9,6,4,2,3,5,7,0,1]
    //[0,1,2,3,4,5,6,7,9]
    public int missingNumberBySort(int[] nums) {
        Arrays.sort(nums);
        for(int i=0;i<nums.length;i++){
            if(i!=nums[i])return i;
        }
        return nums.length;
    }
    //异或
    public int missingNumber(int[] nums) {
        int ret = nums.length;
        for(int i=0;i<nums.length;i++){
            ret^=(i^nums[i]);
        }
        return ret;
    }
}

IP地址与int整数的转换

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66

import java.util.Scanner;
public class Main{
    public long ipAddress2int(String ipAddress) {
        String[] strings = ipAddress.split("\\.");
        StringBuilder sb = new StringBuilder();
        for (String s : strings) {
            Integer of = Integer.valueOf(s);//短除法
            StringBuilder sba = new StringBuilder();
            while (of > 0) {
                int binary = of % 2;
                of = of >> 1;
                sba.append(binary);
            }
            while (sba.length() < 8) sba.append(0);//不满8位前面补0
            sba.reverse();
            sb.append(sba);
        }
        long ret = 0;
        for (int i = sb.length() - 1; i >= 0; i--) {
            int num = sb.charAt(i) - '0';
            ret += (num * Math.pow(2, 31 - i));
        }
        return ret;
    }

    /**
     * 整数转ip
     * @param num
     * @return
     */
    public String int2IpAddress(Long num) {
        StringBuilder sba = new StringBuilder();
        while (num > 0) {
            long binary = num % 2;
            num = num >> 1;
            sba.append(binary);
        }
        while (sba.length() < 32) sba.append(0);//不满8位前面补0
        sba.reverse();

        StringBuilder sb = new StringBuilder();
        //四个八位
        for (int i = 1; i <= 4; i++) {
            int ret = 0;
            for (int j = i * 8 - 1; j >= (i-1)*8; j--) {
                int n = sba.charAt(j) - '0';
                ret += (n * Math.pow(2, (i * 8 - 1) - j));
            }
            sb.append(ret);
            if(i!=4)sb.append(".");
        }
        return sb.toString();
    }

    public static void main(String[] args) {
        try (Scanner scanner = new Scanner(System.in)) {
            while (scanner.hasNext()) {
                String ipAddress = scanner.nextLine();
                Long number = Long.valueOf(scanner.nextLine());
                System.out.println(new Main().ipAddress2int(ipAddress));
                System.out.println(new Main().int2IpAddress(number));
            }
        }
    }
}

762. 二进制表示中质数个计算置位（easy）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
    public int countPrimeSetBits(int left, int right) {
        int ret = 0;
        while(left<=right){
            //1.获取left二进制中1的个数
            int num = left;
            int sit = 0;
            while(num>0){
                sit+=num&1;
                num>>=1;
            }
            //2.判断是否是质数
            if(isPrimeNumber(sit))ret++;
            left++;
        }
        return ret;
    }
    public boolean isPrimeNumber(int num){
        if(num==2)return true;
        if(num<2||num%2==0)return false;
        for(int i=3;i<=Math.sqrt(num);i+=2){
            if(num%i==0)return false;
        }
        return true;
    }
}

6186. 按位或最大的最小子数组长度（mid）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
    //1,1,0,2,1,3
    //对应的二进制(纵向)
    //0 0 0 1 0 1
    //1 1 0 0 1 1
    //分析：从后向前遍历,因为是或只要有一位是1即会更大,且只需要考虑里当前位置最近的'1'位,
    //案例：当后向前遍历到倒数第二个1(01)时,其后面所有的按位或为3(11),此时我们发现其实我们只要和2进行或就可以了,1|0|2 = 3(11)
    //结论：我们只需要取里当前位最近的那个1
    //实现：使用一个长度为32数组来记录每一位最近的那个1位置,如果当前数的位是1则更新,最后作差获取距离
    public int[] smallestSubarrays(int[] nums) {
        int n = nums.length;
        int[] dp = new int[32];//记录每一位最近的那个1
        int[] ret = new int[n];
        for(int i = n - 1;i>=0;i--){
            int dist = 1;
            for(int j=31;j>=0;j--){
                if((nums[i]&1)==1){//如果当前位是1则更新最近的1
                    dp[j] = i;
                } else if(dp[j]>0){
                    dist = Math.max(dp[j] - i + 1,dist);
                }
                nums[i]>>=1;
            }
            ret[i] = dist;
        }
        return ret;
    }
}

相关资料

基础算法 > 刷题记录
刷题笔记-位运算/进制转换
https://mikeygithub.github.io/2020/11/19/yuque/算法笔记-位运算!进制转换/
作者
Mikey
发布于
2020年11月19日
许可协议