刷题笔记-二分搜索

image.png

二分查找

模板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class BinarySearch{
   public int[] binarySearch(int[] nums,int target){ 
       int left = 0,right = ...;
       while (...){
           int mid = left+(right-left)/2;
           if (nums[mid]==target){
               ...
           }else if (nums[mid]<target){
               left = ...;
           }else if (nums[mid]>target){
               right = ...;
           }
       }
       return ...;
   }
}

细节

1.退出循环的条件left<right和left<=right有什么区别？

1
2
3
4
5
6
7
8
9
可知:
left<right的结束条件是left==right跳出循环,搜索区间为[left,right)
left<=right结束条件是left=right+1跳出循环,搜索区间为[left,right]

解释:                           
因为当left==right已经结束循环了，显而易见当我们取left<right是无法搜索到right这个位置。
                                      
结论:
当right取arr.length时取left<right。当right取arr.length-1时取left<=right。

2.区间缩进left=mid+1和left=mid或（right=mid和right=mid-1）有什么区别？

1
2
3
4
5
6
7
8
可知:
left=mid+1或right=mid-1表示下一轮搜索中搜索区间不包含mid，而left=mid或right=mid是包含mid的。

解释:
这两种方式应用的场景(功能)不一样，left=mid+1或right=mid-1是正常的二分查找使用到，而left=mid或right=mid则是在一些二分搜索的变体中使用

结论:
正常情况下如果我们只有查询数组中是否存在target时只需要left=mid+1或right=mid-1即可。

二分搜索target最左最右索引

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
//查找target最左边的值
public int findLeftBinarySearch(int[] arr,int target){
    int left = 0,right = arr.length;
    while (left<right){
        int mid = left+(right-left)/2;
        if (arr[mid]>=target)right = mid;//找到值依旧往左区间找,right = mid 所以 mid 向左移动
        else if (arr[mid]<target) left = mid+1;//右区间
    }
    return left;//跳出循环时此时left==right,而right正好是target
}
//查找target最右边的值
public int findRightBinarySearch(int[] arr,int target){
    int left = 0,right = arr.length;
    while (left<right){
        int mid = left+(right-left)/2;
        if (arr[mid]>target)right = mid;//左区间
        else if (arr[mid]<=target) left = mid+1;//找到值依旧往右区间找
    }
    return left-1;//跳出循环时此时left==right,我们使用left记录target的,所以此时需要-1
}

3.取下标的mid=(left+right)/2和mid=left+(right-left)/2有什么区别？

1
这两种写法本质上没有什么区别，结果都一样，但是后者能防止整数溢出

相关题目

x 的平方根(简单)

二分查找

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    public int mySqrt(int x) {
        int l = 0, r = x, ans = -1;
        while (l <= r) {
            int mid = l + (r - l) / 2;
            if ((long) mid * mid <= x) {
                ans = mid;
                l = mid + 1;
            } else {
                r = mid - 1;
            }
        }
        return ans;
    }
}

牛顿迭代法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public int mySqrt(int x) {
        if (x == 0) {
            return 0;
        }

        double C = x, x0 = x;
        while (true) {
            double xi = 0.5 * (x0 + C / x0);
            if (Math.abs(x0 - xi) < 1e-7) {
                break;
            }
            x0 = xi;
        }
        return (int) x0;
    }
}

有效的完全平方数(简单)

二分查找

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public boolean isPerfectSquare(int num) {
    int l = 0, r = num, ans = -1;
        while (l <= r) {
            int mid = l + (r - l) / 2;
            if ((long) mid * mid == num) {
                return true;
            }else if ((long) mid * mid <= num) {
                ans = mid;
                l = mid + 1;
            } else {
                r = mid - 1;
            }
        }
        return false;
    }
}

搜索旋转排序数组(中等)

将数组一分为二，其中一定有一个是有序的，另一个可能是有序，也能是部分有序。 此时有序部分用二分法查找。无序部分再一分为二，其中一个一定有序，另一个可能有序，可能无序。就这样循环. 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    //思路：将数组一分为二，其中一定有一个是有序的，另一个可能是有序，也能是部分有序。此时有序部分用二分法查找。
    //无序部分再一分为二，其中一个一定有序，另一个可能有序，可能无序。就这样循环.
    public int search(int[] nums, int target) {
        if(nums.length==0)return -1;
        if(nums.length==1)return nums[0]==target?0:-1;
        int left = 0,right = nums.length-1;
        while(left<=right){
            int mid = (left+right)/2;
            if(nums[mid]==target)return mid;
            if(nums[0]<=nums[mid]){//左区间有序
                if(nums[0]<=target&⌖<nums[mid])right=mid-1;//target在左区间
                else left=mid+1;
            }else{//右区间有序
                if(nums[nums.length-1]>=target&⌖>nums[mid])left=mid+1;//target在右区间
                else right=mid-1;
            }
        }
        return -1;
    }
}

搜索二维矩阵(中等)

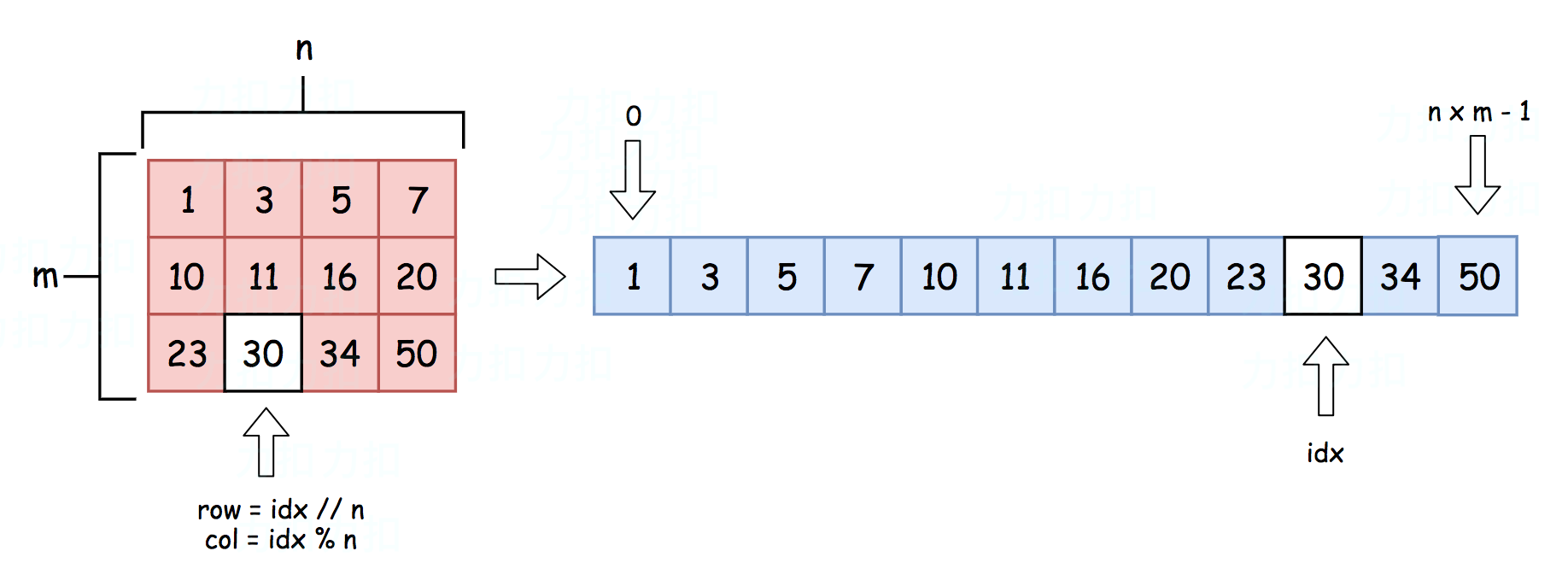
二分查找，将其看做一个有序一维数组,row = idx / n ， col = idx % n

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
  public boolean searchMatrix(int[][] matrix, int target) {
    int m = matrix.length;
    if (m == 0) return false;
    int n = matrix[0].length;

    // 二分查找
    int left = 0, right = m * n - 1;
    int pivotIdx, pivotElement;
    while (left <= right) {
      pivotIdx = (left + right) / 2;
      pivotElement = matrix[pivotIdx / n][pivotIdx % n];
      if (target == pivotElement) return true;
      else {
        if (target < pivotElement) right = pivotIdx - 1;
        else left = pivotIdx + 1;
      }
    }
    return false;
  }
}

搜索二维矩阵(中等)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
    /**
     *左下角的元素是这一行中最小的元素，同时又是这一列中最大的元素。比较左下角元素和目标：
若左下角元素等于目标，则找到
若左下角元素大于目标，则目标不可能存在于当前矩阵的最后一行，问题规模可以减小为在去掉最后一行的子矩阵中寻找目标
若左下角元素小于目标，则目标不可能存在于当前矩阵的第一列，问题规模可以减小为在去掉第一列的子矩阵中寻找目标
若最后矩阵减小为空，则说明不存在 
     */
    public boolean searchMatrix(int[][] matrix, int target) { 
        int x=matrix.length-1,y=0;
        while(x>=0&&y<matrix[0].length){
            if(matrix[x][y]==target){
                return true;
            }
            if(matrix[x][y]>target){
                x--;
            }else{
                y++;
            }
        }
        return false;
    }
}

寻找旋转排序数组中的最小值(中等)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
    public int search(int[] nums, int target) {
        int n = nums.length;
        if (n == 0) {
            return -1;
        }
        if (n == 1) {
            return nums[0] == target ? 0 : -1;
        }
        //二分查找
        int l = 0, r = n - 1;
        while (l <= r) {
            int mid = (l + r) / 2;
            if (nums[mid] == target) {//是目标值直接返回
                return mid;
            }
            if (nums[0] <= nums[mid]) {//当前是单调递增区间
                if (nums[0] <= target && target < nums[mid]) {//0-mid区间
                    r = mid - 1;
                } else {//mid-r区间
                    l = mid + 1;
                }
            } else {//当前不是单调递增区间
                if (nums[mid] < target && target <= nums[n - 1]) {//(mid)-(n-1)区间
                    l = mid + 1;
                } else {//l-mid区间
                    r = mid - 1;
                }
            }
        }
        return -1;
    }
}

递增的三元子序列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
class Solution {
    //双向遍历
    public boolean increasingTriplet(int[] nums) {
        int n = nums.length;
        if (n < 3) {
            return false;
        }
        int[] leftMin = new int[n];
        leftMin[0] = nums[0];
        for (int i = 1; i < n; i++) {
            leftMin[i] = Math.min(leftMin[i - 1], nums[i]);
        }
        int[] rightMax = new int[n];
        rightMax[n - 1] = nums[n - 1];
        for (int i = n - 2; i >= 0; i--) {
            rightMax[i] = Math.max(rightMax[i + 1], nums[i]);
        }
        for (int i = 1; i < n - 1; i++) {
            if (nums[i] > leftMin[i - 1] && nums[i] < rightMax[i + 1]) {
                return true;
            }
        }
        return false;
    }
    //贪心
    public boolean increasingTriplet(int[] nums) {
        int n = nums.length;
        if (n < 3) return false;
        int first = nums[0], second = Integer.MAX_VALUE;
        for (int i = 1; i < n; i++) {
            int num = nums[i];
            if (num > second) {//遇到比第二个数大的直接返回结果
                return true;
            } else if (num > first) {//否则first<num<=second更新second
                second = num;
            } else {//否则num<=first更新first
                first = num;
            }
        }
        return false;
    }
}

寻找两个正序数组的中位数（hard)

一般只要是要求时间复杂度是O(log(m+n))的都是使用二分查找来实现。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
/**
     * 分割线的特点：
     * 1.m+n未偶数则取分割线左右两边的最近一个数求和/2得出中位数。
     * 2.m+n为奇数则分割线左边的那是数就是中位数。
     * 3.num1,num2的分割线左边总个数大致等于右边总个数(m+n等于奇数时多一，偶数相等)
     * 4.num1的分割线左边最大值(靠近分割线那个值)满足小于num2的分割线右边最小值(靠近分割线那个值)。
     *   同样的num2的分割线左边最大值(靠近分割线那个值)满足小于num1的分割线右边最小值(靠近分割线那个值)
     *   即：nums1[i-1] <= nums2[j] && nums2[j-1] <= nums1[i]
     *
     * 怎么找这两个数组的分割线：
     * 1.通过使用二分查找，确定num1的分割线i，num2分割线j。如果nums1[i-1] > nums2[j] 则说明分割线在 i-1左边，否则在右边
     *
     * @param nums1
     * @param nums2
     * @return
     */
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        // 始终保证nums1为较短的数组，nums1过长可能导致j为负数而越界
        if (nums1.length > nums2.length) {
            int[] temp = nums1;
            nums1 = nums2;
            nums2 = temp;
        }

        int m = nums1.length;
        int n = nums2.length;

        // m+n 为奇数，分割线要求左侧有 (m+n)/2 + 1 个元素
        // m+n 为偶数，分割线要求左侧有 (m+n)/2     个元素
        // 两种情况其实可以统一写作 (m+n+1)/2，表示对(m+n)/2向上取整
        // 对整数来说，向上取整等于：(被除数 + (除数 - 1)) / 除数
        // 也可以使用Math类中提供的库函数
        int leftTotal = (m + n + 1) / 2;
        int left = 0, right = m;
        while (left < right) {
            // +1 向上取整避免 left + 1 = right 时可能无法继续缩小区间而陷入死循环
            int i = left + (right - left + 1) / 2;
            int j = leftTotal - i;

            //要找最大i，使得nums1[i-1] <= nums2[j]
            //使用对立面缩小区间
            if (nums1[i - 1] > nums2[j]) {
                // [i+1, m]均不满足
                right = i - 1;
            } else {
                // i满足说明[0, i-1]均不为满足条件的最大i，舍去以缩小区间
                left = i;
            }
        }
        //退出循环时left=right，表示最终nums1中分割线的位置
        int i = left;
        //nums2中分割线的位置
        int j = leftTotal - left;//因为相对而言合并两个数组后的分割线左边元素个数为(m + n + 1) / 2

        //判断极端情况
        int nums1LeftMax = (i == 0) ? Integer.MIN_VALUE : nums1[i - 1];  //nums1分割线左边没有元素
        int nums2LeftMax = (j == 0) ? Integer.MIN_VALUE : nums2[j - 1];  //nums2分割线左边没有元素
        int nums1RightMin = (i == m) ? Integer.MAX_VALUE : nums1[i];     //nums1分割线右边没有元素
        int nums2RightMin = (j == n) ? Integer.MAX_VALUE : nums2[j];     //nums2分割线右边没有元素

        if (((m + n) % 2) == 1) return Math.max(nums1LeftMax, nums2LeftMax);
        else return (double) ((Math.max(nums1LeftMax, nums2LeftMax) + Math.min(nums1RightMin, nums2RightMin))) / 2;
    }

see：https://leetcode-cn.com/problems/median-of-two-sorted-arrays/solution/he-bing-yi-hou-zhao-gui-bing-guo-cheng-zhong-zhao-/

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
class Solution {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        int leftLength = nums1.length;
        int rightLength = nums2.length;
        // 为了保证第一个数组比第二个数组小(或者相等)
        if (leftLength > rightLength) {
            return findMedianSortedArrays(nums2, nums1);
        }
        // 分割线左边的所有元素需要满足的个数 m + (n - m + 1) / 2;
        // 两个数组长度之和为偶数时，当在长度之和上+1时，由于整除是向下取整，所以不会改变结果
        // 两个数组长度之和为奇数时，按照分割线的左边比右边多一个元素的要求，此时在长度之和上+1，就会被2整除，会在原来的数
        //的基础上+1，于是多出来的那个1就是左边比右边多出来的一个元素
        int totalLeft = (leftLength + rightLength + 1) / 2;
        // 在 nums1 的区间 [0, leftLength] 里查找恰当的分割线，
        // 使得 nums1[i - 1] <= nums2[j] && nums2[j - 1] <= nums1[i]
        int left = 0;
        int right = leftLength;
        // nums1[i - 1] <= nums2[j]
        //  此处要求第一个数组中分割线的左边的值 不大于(小于等于) 第二个数组中分割线的右边的值
        // nums2[j - 1] <= nums1[i]
        //  此处要求第二个数组中分割线的左边的值 不大于(小于等于) 第一个数组中分割线的右边的值
        // 循环条件结束的条件为指针重合，即分割线已找到
        while (left < right) {
            // 二分查找，此处为取第一个数组中左右指针下标的中位数，决定起始位置
            // 此处+1首先是为了不出现死循环，即left永远小于right的情况
            // left和right最小差距是1，此时下面的计算结果如果不加1会出现i一直=left的情况，而+1之后i才会=right
            // 于是在left=i的时候可以破坏循环条件，其次下标+1还会保证下标不会越界，因为+1之后向上取整，保证了
            // i不会取到0值，即i-1不会小于0
            // 此时i也代表着在一个数组中左边的元素的个数
            int i = left + (right - left + 1) / 2;
            // 第一个数组中左边的元素个数确定后，用左边元素的总和-第一个数组中元素的总和=第二个元素中左边的元素的总和
            // 此时j就是第二个元素中左边的元素的个数
            int j = totalLeft - i;
            // 此处用了nums1[i - 1] <= nums2[j]的取反，当第一个数组中分割线的左边的值大于第二个数组中分割线的右边的值
            // 说明又指针应该左移，即-1
            if (nums1[i - 1] > nums2[j]) {
                // 下一轮搜索的区间 [left, i - 1]
                right = i - 1;
                // 此时说明条件满足，应当将左指针右移到i的位置，至于为什么是右移，请看i的定义
            } else {
                // 下一轮搜索的区间 [i, right]
                left = i;
            }
        }
        // 退出循环时left一定等于right，所以此时等于left和right都可以
        // 为什么left一定不会大于right?因为left=i。
        // 此时i代表分割线在第一个数组中所在的位置
        // nums1[i]为第一个数组中分割线右边的第一个值
        // nums[i-1]即第一个数组中分割线左边的第一个值
        int i = left;
        // 此时j代表分割线在第二个数组中的位置
        // nums2[j]为第一个数组中分割线右边的第一个值
        // nums2[j-1]即第一个数组中分割线左边的第一个值
        int j = totalLeft - i;
        // 当i=0时，说明第一个数组分割线左边没有值，为了不影响
        // nums1[i - 1] <= nums2[j] 和 Math.max(nums1LeftMax, nums2LeftMax)
        // 的判断，所以将它设置为int的最小值
        int nums1LeftMax = i == 0 ? Integer.MIN_VALUE : nums1[i - 1];
        // 等i=第一个数组的长度时，说明第一个数组分割线右边没有值，为了不影响
        // nums2[j - 1] <= nums1[i] 和 Math.min(nums1RightMin, nums2RightMin)
        // 的判断，所以将它设置为int的最大值
        int nums1RightMin = i == leftLength ? Integer.MAX_VALUE : nums1[i];
        // 当j=0时，说明第二个数组分割线左边没有值，为了不影响
        // nums2[j - 1] <= nums1[i] 和 Math.max(nums1LeftMax, nums2LeftMax)
        // 的判断，所以将它设置为int的最小值
        int nums2LeftMax = j == 0 ? Integer.MIN_VALUE : nums2[j - 1];
        // 等j=第二个数组的长度时，说明第二个数组分割线右边没有值，为了不影响
        // nums1[i - 1] <= nums2[j] 和 Math.min(nums1RightMin, nums2RightMin)
        // 的判断，所以将它设置为int的最大值
        int nums2RightMin = j == rightLength ? Integer.MAX_VALUE : nums2[j];
        // 如果两个数组的长度之和为奇数，直接返回两个数组在分割线左边的最大值即可
        if (((leftLength + rightLength) % 2) == 1) {
            return Math.max(nums1LeftMax, nums2LeftMax);
        } else {
            // 如果两个数组的长度之和为偶数，返回的是两个数组在左边的最大值和两个数组在右边的最小值的和的二分之一
            // 此处不能被向下取整，所以要强制转换为double类型
            return (double) ((Math.max(nums1LeftMax, nums2LeftMax) + Math.min(nums1RightMin, nums2RightMin))) / 2;
        }
    }
}

在排序数组中查找元素的第一个和最后一个位置

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    //思路：O(logn)二分查找target左右边界
    //如何查找边界：查找左边界，查找到值继续向左区间搜索，直到退出循环，查找右边届同理
    public int[] searchRange(int[] nums, int target) {
        int left = 0,right = nums.length-1;
        int[] ans = {-1,-1};
        if(nums.length==0)return ans;
        while(left<right){
            int mid = left+(right-left)/2;
            if(nums[mid]>=target)right = mid;
            else left = mid + 1;
        }
        if(nums[left]!=target)return ans;
        ans[0] = left;
        right = nums.length;
        while(left<right){
            int mid = left+(right-left)/2;
            if(nums[mid]<=target)left = mid + 1;
            else right = mid;
        }
        ans[1] = left - 1;
        return ans;
    }
}

寻找旋转排序数组中的最小值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
class Solution {
    //思路：二分变体
    //查找第一个递减的区间
    public int findMin(int[] nums) {
        int left = 0 ,right = nums.length-1;
        if(nums[0]<nums[right]||right==0)return nums[0];
        while(left<=right){
            int mid = left+(right-left)/2;
            if(nums[mid]>nums[mid+1])return nums[mid+1];
            if(nums[mid-1]>nums[mid])return nums[mid];
            if(nums[left]<nums[mid]){
                left=mid+1;
            }else{
                right=mid-1;
            }
        }
        return nums[0];
    }
    //旋转后数组可能是的状态：
    //1.整个数组呈递增状态(旋转了n次n=num.length)
    //2.数组呈现两段(左段、右段)递增，必定是左段的数组都大于右段

    //针对上述两种情况(2其实包含了1),mid可能出现的情况：
    //1.nums[mid]<nums[left],说明mid在右段，且因为右段的所有数必定小于左段，所以min必定在(left,mid]区间，令right = mid
    //2.nums[mid]>=num[left],说明mid在左段，而左段必定大于右段，所以 min必定在(mid,right]区间，令left = mid + 1
    public int findMin(int[] nums) {
        int left = 0, right = nums.length - 1;
        while(left<right){
            int mid = left + (right-left)/2;
            if(nums[mid]<nums[right]){
                right = mid;
            }else{
                left = mid + 1;
            }
        }
        return nums[left];
    }
}

寻找峰值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
    //思路：O(log n) 二分查找
    //条件：nums[-1] = nums[n] = -∞ 
    //证明：如果存在nums[mid] < nums[mid+1] 基于条件可知往右边继续查找必定能找到右峰底
    //会有两种情况
    //1.nums[mid+2]直接小于nums[mid+1],则峰顶就是nums[mid+1]
    //2.nums[mid+1,n-1]都是升序，基于条件，那么是右峰底就是nums[n]，此时nums[n-2],nums[n-1],nums[n]构成山峰
    //结论：
    //1.如果nums[i] > nums[i+1]，则在i之前一定存在峰值元素
    //2.如果nums[i] < nums[i+1]，则在i+1之后一定存在峰值元素
    public int findPeakElement(int[] nums) {
        int left =0 ,right = nums.length-1;
        while(left<right){
            int mid = left+(right-left)/2;
            if (nums[mid] < nums[mid+1]) {
                left = mid + 1;
            } else {
                right = mid;
            }
        }
        return left;
    }
}

最长公共前缀

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
class Solution {
    //横向比较
    public String longestCommonPrefix(String[] strs) {
        StringBuilder sb = new StringBuilder();
        for(int i=0;i<strs[0].length();i++){
            char c = strs[0].charAt(i);
            for(String s:strs){
                if(s.length()<=i||s.charAt(i)!=c)return sb.toString();
            }
            sb.append(c);
        }
        return sb.toString();
    }
    //二分查找
    public String longestCommonPrefix0(String[] strs) {
        if (strs == null || strs.length == 0) return "";
        int minLength = Integer.MAX_VALUE;
        for (String str : strs) minLength = Math.min(minLength, str.length());
        int low = 0, high = minLength;
        while (low < high) {
            int mid = (high - low + 1) / 2 + low;
            if (isCommonPrefix(strs, mid)) {
                low = mid;
            } else {
                high = mid - 1;
            }
        }
        return strs[0].substring(0, low);
    }

    public boolean isCommonPrefix(String[] strs, int length) {
        String str0 = strs[0].substring(0, length);
        int count = strs.length;
        for (int i = 1; i < count; i++) {
            String str = strs[i];
            for (int j = 0; j < length; j++) {
                if (str0.charAt(j) != str.charAt(j)) {
                    return false;
                }
            }
        }
        return true;
    }
}

长度最小的子数组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
class Solution {
    //暴力破解
    public int minSubArrayLen(int s, int[] nums) {
        int n = nums.length;
        if (n == 0) return 0;
        int ans = Integer.MAX_VALUE;
        for (int i = 0; i < n; i++) {
            int sum = 0;
            for (int j = i; j < n; j++) {
                sum += nums[j];
                if (sum >= s) {
                    ans = Math.min(ans, j - i + 1);
                    break;
                }
            }
        }
        return ans == Integer.MAX_VALUE ? 0 : ans;
    }
    //前缀和+二分查找
    public int minSubArrayLen(int s, int[] nums) {
        int n = nums.length;
        if (n == 0) return 0;
        int ans = Integer.MAX_VALUE;
        int[] sums = new int[n + 1];
        // 为了方便计算，令 size = n + 1
        // sums[0] = 0 意味着前 0 个元素的前缀和为 0
        // sums[1] = A[0] 前 1 个元素的前缀和为 A[0]
        // 以此类推
        for (int i = 1; i <= n; i++) sums[i] = sums[i - 1] + nums[i - 1];
        for (int i = 1; i <= n; i++) {
            int target = s + sums[i - 1];
            int bound = Arrays.binarySearch(sums, target);
            if (bound < 0) {
                bound = -bound - 1;
            }
            if (bound <= n) {
                ans = Math.min(ans, bound - (i - 1));
            }
        }
        return ans == Integer.MAX_VALUE ? 0 : ans;
    }
}

有序数组中的单一元素

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
    //思路：二分查找
    //二分每次将分为两个部分，通过mid的奇偶判断在左右区间，如果mid%2==0&&nums[mid]==nums[mid+1]说明在右区间反之
    public int singleNonDuplicate(int[] nums) {
        int n = nums.length;
        int left = 0,right = n - 1;
        while(left<=right){
            int mid = left+(right-left)/2;
            if(mid%2==0){
                if(mid<n-1&&nums[mid]==nums[mid+1]){
                    left = mid + 2;
                }else {
                	right = mid - 2;
                }
            }else{
                if(mid>0&&nums[mid]==nums[mid-1]){
                    left = mid + 1;
                }else {
                	right = mid - 1;
                }
            }
        }
        return nums[left];
    }
}

第 N 位数字

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
class Solution {
    //思路：根据数的位数和数的个数可知
    //1~9 有 1位*9个=9个
    //10~99 有 2位*90个=180个
    //100~999 有 3位*900个=2700个
    //由此可以来确定n具体落在那个数上，通过二分不断确定其所在的位置
    //例如如查找407
    //通过上面的递推可知其区间在(100,999)
    public int findNthDigit(int n) {
        //二分查找所在的范围
        int low = 1,height = 9;
        while (low<height){
            int mid = low + (height-low)/2;
            if(totalDigit(mid)<n){
                low = mid+1;
            }else {
                height = mid;
            }
        }
        //右一个长度拥有的数的数量
        int d = low;
        //前一个长度拥有的数的数量
        int prevDigits = totalDigit(d-1);
        //获取n在数字位数为d的所在下标(单个字符)的位置（100,101,102），-1是为了下标从0开始
        int index = n - prevDigits - 1;
        //左区间,如100,1000
        int start = (int)Math.pow(10,d-1);
        //在第几个数(整数)
        int num = start + index / d;
        //取模得出在一个整数数中的第几位(单个字符)数。如100,d=2则100%2=0,在第0位
        int digitIndex = index % d;
        //得出在第几个数(num)的下标为第几位(digitIndex)即可求出答案 如132的下标为2位,(132/(3-2-1))%10=2
        int digit = (num/(int) (Math.pow(10,d - digitIndex -1))) % 10;//
        return digit;
    }
    //获取长度为length所包含的数的量
    public int totalDigit(int length){
        int digit = 0;
        int curLength = 1,curCount = 9;
        while (curLength<=length){
            digit+=curLength*curCount;
            curLength++;
            curCount*=10;
        }
        return digit;
    }
}

山脉数组中查找目标值（hard）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Solution {
    //思路:二分查找(注意题目中的山脉是单个山脉所以可以通过二分进行查找峰顶，在二分查找左右两边)
    public int findInMountainArray(int target, MountainArray mountainArr) {
        int n = mountainArr.length();
        int left = 0,mid = 0,right = n - 1;
        //1.查找山峰
        while(left<right){
            mid = left+(right-left)/2;
            int midN = mountainArr.get(mid);
            int midL = mountainArr.get(mid-1);
            int midR = mountainArr.get(mid+1);
            if(midL<midN&&midR<midN)break;
            else if(midL<midN&&midR>midN){
                left = mid;
            }else{
                right = mid;
            }
        }
        //2.二分查找上坡
        int l = 0,r = mid;
        while(l<=r){
            int m = l+(r-l)/2;
            int mN = mountainArr.get(m);
            if(mN==target)return m;
            else if(mN>target)r=m-1;
            else if(mN<target)l=m+1;
        }
        //3.上坡未查到查下坡
        int le = mid,ri = n-1;
        while(le<=ri){
            int m = le+(ri-le)/2;
            int mN = mountainArr.get(m);
            if(mN==target)return m;
            else if(mN>target)le=m+1;
            else if(mN<target)ri=m-1;
        }
        return -1;
    }
}

875. 爱吃香蕉的珂珂（mid）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
    //[4,11,20,23,30]
    //每次只能选一堆,设piles长度为n,至少需要吃n次,最多可以吃h次
    //ret取值范围[1,max(piles)],通过二分确定其在这个区间的范围。
    public int minEatingSpeed(int[] piles, int h) {
        int n = piles.length;
        int left = 1;
        int max = 0;
        for(int p:piles)max=Math.max(max,p);
        int right = max;
        while(left<right){
            int mid = (left+right)>>>1;
            int needHourse = 0;
            for(int p:piles)needHourse+=(p-1)/mid+1;
            if(needHourse>h){//需要吃更多
                left = mid + 1;
            } else {//还有时间,可继续减少吃的速度
                right = mid;
            }
        }
        return left;
    }
}

668. 乘法表中第k小的数（hard）

1 2 3 4 5 6
2 4 6 8 10 12
3 6 9 12 15 18
4 8 12 16 20 24
5 10 15 20 25 30
6 12 18 24 30 36

求第几小等价于求有多少数字不超过 x（求x）。我们可以遍历乘法表的每一行，对于乘法表的第 i 行，其数字均为 i 的倍数，因此不超过 x 的数字有 所以整个乘法表不超过 x 的数字个数为由于时上式可化简为由于 x 越大上式越大，x 越小上式越小，因此我们可以二分 x 找到答案，二分的初始边界为乘法表的元素范围，即 [1,mn]。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public int findKthNumber(int m, int n, int k) {
        //设置左右边界
        int left = 1, right = m * n;
        while (left < right) {
            int x = left + (right - left) / 2;
            //获取当前比x小的个数count
            int count = x / n * n;
            for (int i = x / n + 1; i <= m; ++i) {
                count += x / i;
            }
            //如果count大于k说明在左区间
            if (count >= k) {
                right = x;
            } else {//否则在右区间
                left = x + 1;
            }
        }
        return left;
    }
}

719. 找出第 K 小的数对距离（hard）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution {
        // 1 3 4 7 8 11 left=0, right=max-min=11-1=10, mid=5
    // 整数区间 [3, 4, 6, 9]，最小数 3 和最大数 9 的差为 6。这个整数区间里的 所有 数对的差值都小于等于 6。
    // 基于这一点，我们就可以一下子计算出小于等于 6 的数对的个数，C^2_4 = (4*3)/(2*1) = 6 ,即 4 个元素任意取 2 个的组合数为 6 个。
    public int smallestDistancePair(int[] nums, int k) {
        int n = nums.length;
        Arrays.sort(nums);//nlog(n)
        int left = 0,right = nums[n-1]-nums[0];
        while (left<right){
            int mid = left+(right-left)/2;
            int count = countLessEquals(nums,mid);
            if (count<k){//如果count（小于等于mid的个数）小于k则说明mid小了
                left = mid + 1;
            }else {//否则向左逼近
                right = mid;
            }
        }
        return left;
    }
    //滑动窗口
    //统计距离（数值之差的绝对值）小于等于 threshold 的个数
    public int countLessEquals(int[] nums,int threshold){
        int count = 0; 
        int length = nums.length; 
        for (int left = 0, right = 0; right < length; right++) { 
            while (nums[right] - nums[left] > threshold) { 
                left++; 
            } 
            // 此时满足 nums[right] - nums[left] <= threshold 
            // right 与 [left..right - 1] 里的每一个元素的「距离」都小于等于 threshold 
            // [left..right - 1] 里元素的个数为 right - left 
            count += right - left; 
        } 
        return count;
    }
}

相关资料

基础算法 > 刷题记录
刷题笔记-二分搜索
https://mikeygithub.github.io/2020/09/01/yuque/算法笔记-二分搜索/
作者
Mikey
发布于
2020年9月1日
许可协议