算法笔记-图论类型

image.png

理论知识

  • 有向图/无向图

    在图中，若节点的边用箭头标明了边是有方向性的，则称这样的图为有向图，否则称为无向图。

  • 出入度

    在有向图中边的箭头指入的节点数量则为该节点的入度，从该节点指出的边则称为出度。

  • 权重

    图中边所标记的数

图的遍历

和多叉树的遍历很相似

  • bfs/dfs
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    56
    57
    58
    59
    60
    61
    class Graph{
        int v;
        private List<Integer> adj[];
        public Graph(int num){
            v = num;
            adj = new LinkedList[v];
            for (int i = 0; i < num; i++) adj[i] = new LinkedList<>();
        }
        public void addEdge(int v,int w){
            adj[v].add(w);
        }
        //借助队列:每轮将当前轮遍历，将自节点入队列
        void bfs(int s){
            boolean[] visited = new boolean[v];
            LinkedList<Integer> queue = new LinkedList<>();
            visited[s]=true;
            queue.add(s);
            while (!queue.isEmpty()){
                Integer poll = queue.poll();
                System.out.println(poll);//输出遍历的节点
                List<Integer> edges = adj[poll];
                for (Integer edge : edges) {
                    if (!visited[edge]){
                        visited[edge]=true;
                        queue.offer(edge);
                    }
                }
            }
        }
        //借助栈:一直压栈直到，弹栈后遇到没遍历过的再次压栈，如此反复
        void dfs(int s){
            boolean[] visited = new boolean[v];
            Stack<Integer> stack = new Stack<>();
            visited[s]=true;
            stack.push(s);
            while (!stack.isEmpty()){
                Integer poll = stack.pop();
                System.out.println(poll);
                List<Integer> edges = adj[poll];
                for (Integer edge : edges) {
                    if (!visited[edge]){
                        visited[edge]=true;
                        stack.push(edge);
                    }
                }
            }
        }
    }

    public static void main(String[] args) {
        Graph g = new Graph(4);
        g.addEdge(0, 1);
        g.addEdge(0, 2);
        g.addEdge(1, 2);
        g.addEdge(2, 0);
        g.addEdge(2, 3);
        g.addEdge(3, 3);
        System.out.println("Following is Breadth First Traversal (starting from vertex 2)");
        g.bfs(2);
        g.dfs(2);
    }

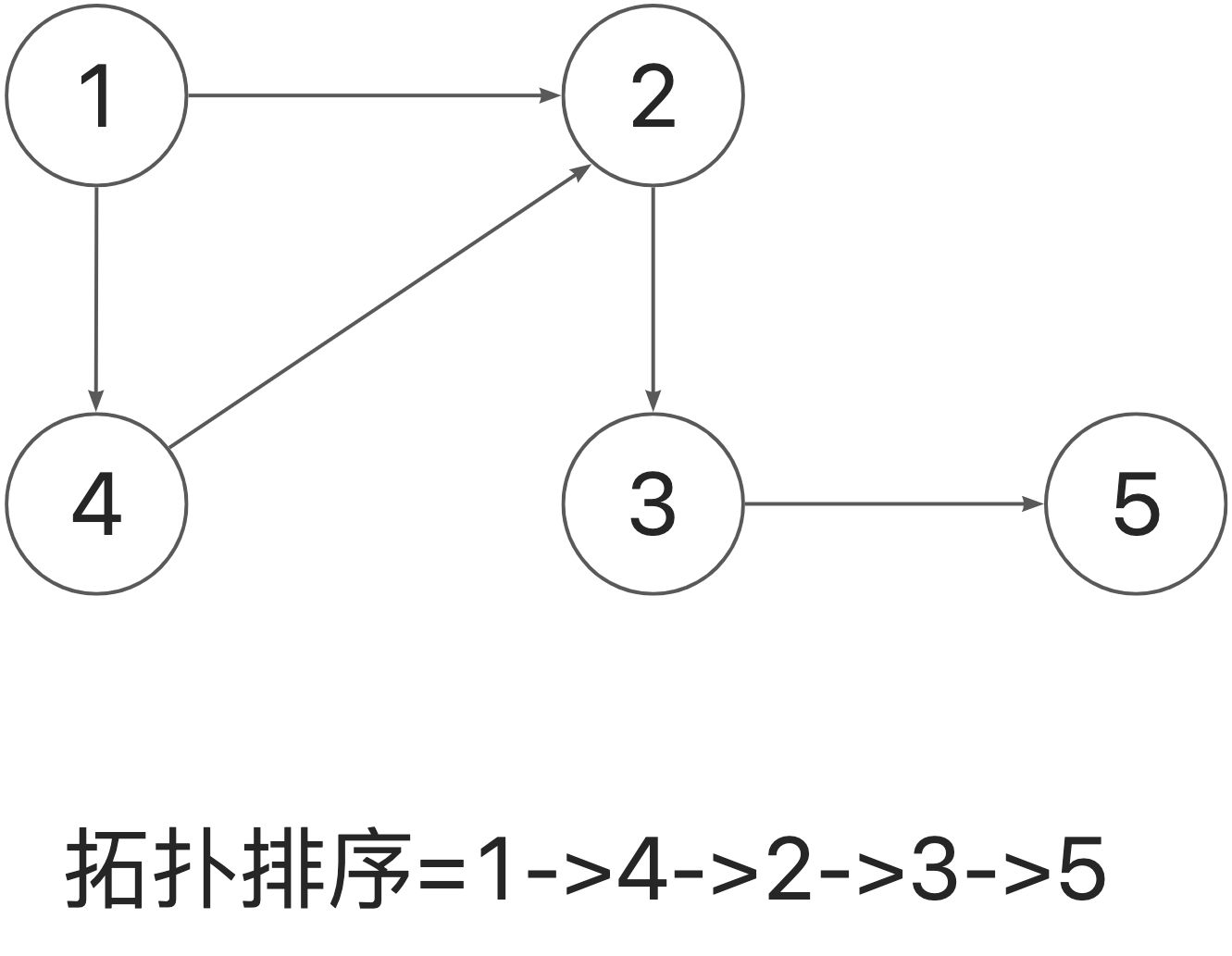
拓扑排序

对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序，是将G中所有顶点排成一个线性序列，使得图中任意一对顶点u和v，若边<u,v>∈E(G)，则u在线性序列中出现在v之前。通常，这样的线性序列称为满足拓扑次序(Topological Order)的序列，简称拓扑序列。简单的说，由某个集合上的一个偏序得到该集合上的一个全序，这个操作称之为拓扑排序。

实现拓扑的步骤

  • 选择一个无前驱的节点开始（入度为0的节点）
  • 从图中删除此顶点及所有出边。

重复上述两个步骤

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
public class Graph {
    private int V;
    private ArrayList<ArrayList<Integer>> adj;
    
    Graph(int v) {
        V = v;
        adj = new ArrayList<>(v);
        for (int i = 0; i < v; ++i) adj.add(new ArrayList<>());//边,下标->目标节点List[]
    }
    /**
     *  添加边
     * @param v 源节点
     * @param w 目标节点
     */
    void addEdge(int v, int w) {
        adj.get(v).add(w);
    }
    
    void topologicalSort(int v, boolean visited[], Stack<Integer> stack) {
        // 标记为已访问
        visited[v] = true;
        Integer i;
        //获取当前节点的所有后继节点
        Iterator<Integer> it = adj.get(v).iterator();
        while (it.hasNext()) {
            i = it.next();
            //未访问过可继续访问
            if (!visited[i]) topologicalSort(i, visited, stack);
        }
        //添加
        stack.push(new Integer(v));
    }
    //拓扑排序
    void topologicalSort() {
        Stack<Integer> stack = new Stack<>();
        // 已访问标记
        boolean visited[] = new boolean[V];
        for (int i = 0; i < V; i++) {
            if (visited[i] == false) {//未访问过的才需要访问
                topologicalSort(i, visited, stack);
            }
        }
        //打印结果
        while (stack.empty() == false) System.out.print(stack.pop() + " ");
    }

    public static void main(String args[]) {
        //创建一个6个节点的图
        Graph g = new Graph(6);
        //添加边
        g.addEdge(5, 2);
        g.addEdge(5, 0);
        g.addEdge(4, 0);
        g.addEdge(4, 1);
        g.addEdge(2, 3);
        g.addEdge(3, 1);
        g.topologicalSort();
    }
}

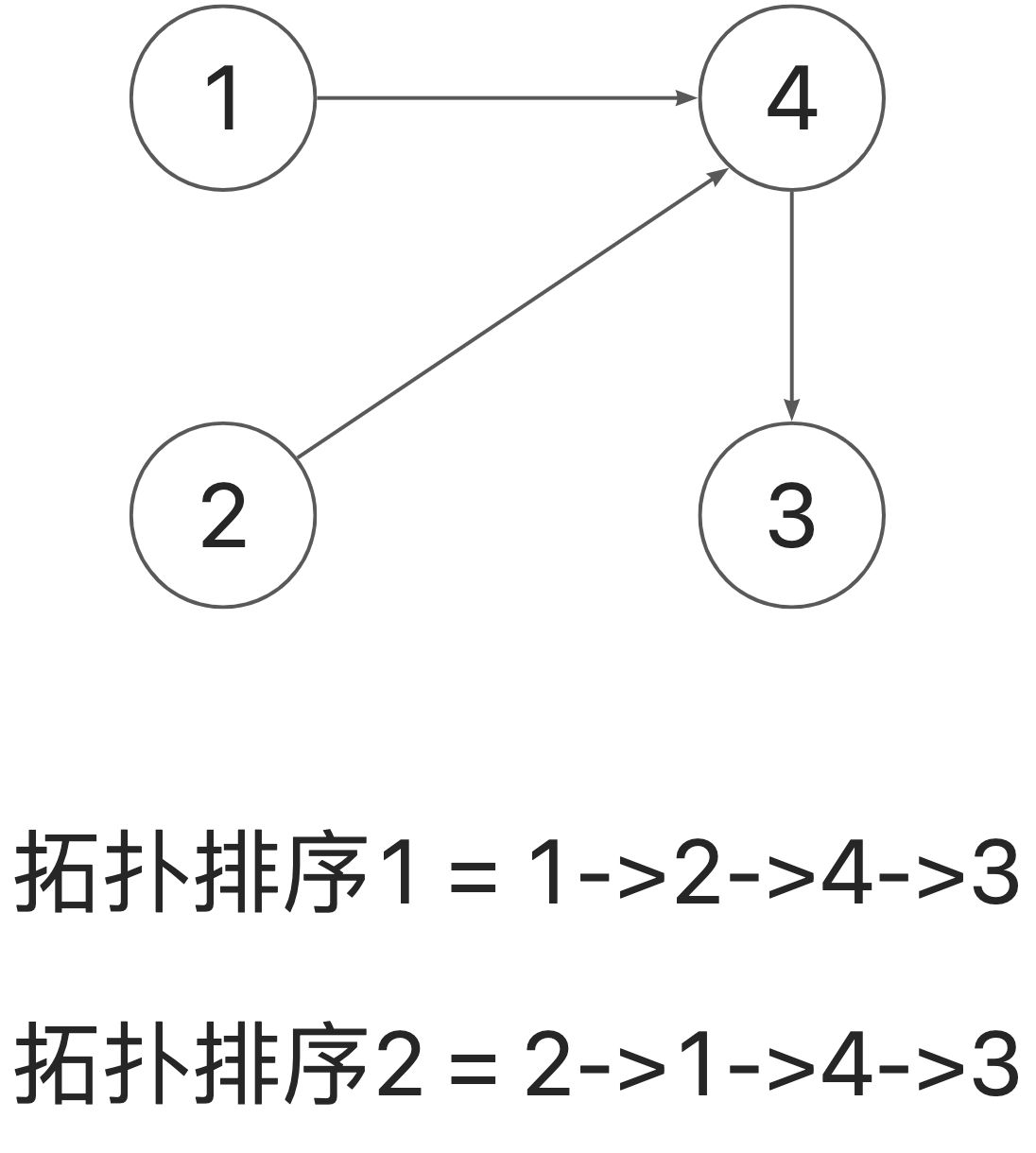
如何维护字典序最小的拓扑序?什么是最小子典序？

简单的理解方法是，把两种解看作两个数字1243 和 2143，小的那个数对应的排列就是字典序偏小的。

相关算法

Dijkstra 算法

最短路径算法

Prim 算法

Kruskal 算法

Bellman-Ford 算法

基于「队列」优化的 Bellman-Ford 算法 — SPFA 算法

拓扑排序之 Kahn 算法

相关题目

到达目的地的第二短时间（hard)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
class Solution {
    public int secondMinimum(int n, int[][] edges, int time, int change) {
        List<Integer>[] graph = new List[n + 1];
        for (int i = 0; i <= n; i++) {
            graph[i] = new ArrayList<Integer>();
        }
        for (int[] edge : edges) {
            graph[edge[0]].add(edge[1]);
            graph[edge[1]].add(edge[0]);
        }

        // path[i][0] 表示从 1 到 i 的最短路长度，path[i][1] 表示从 1 到 i 的严格次短路长度
        int[][] path = new int[n + 1][2];
        for (int i = 0; i <= n; i++) {
            Arrays.fill(path[i], Integer.MAX_VALUE);
        }
        path[1][0] = 0;
        Queue<int[]> queue = new ArrayDeque<int[]>();
        queue.offer(new int[]{1, 0});
        while (path[n][1] == Integer.MAX_VALUE) {
            int[] arr = queue.poll();
            int cur = arr[0], len = arr[1];
            for (int next : graph[cur]) {
                if (len + 1 < path[next][0]) {
                    path[next][0] = len + 1;
                    queue.offer(new int[]{next, len + 1});
                } else if (len + 1 > path[next][0] && len + 1 < path[next][1]) {
                    path[next][1] = len + 1;
                    queue.offer(new int[]{next, len + 1});
                }
            }
        }

        int ret = 0;
        for (int i = 0; i < path[n][1]; i++) {
            if (ret % (2 * change) >= change) {
                ret = ret + (2 * change - ret % (2 * change));
            }
            ret = ret + time;
        }
        return ret;
    }
}

克隆图（medium）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
class Solution {
    //bfs
    //记录节点是否已经克隆:key=旧节点，value=新clone的节点
    private HashMap <Node, Node> visited = new HashMap <> ();
    public Node cloneGraphDFS(Node node) {
        if (node == null) return node;
        // 如果该节点已经被访问过了，则直接从哈希表中取出对应的克隆节点返回
        if (visited.containsKey(node)) return visited.get(node);
        // 克隆节点，注意到为了深拷贝我们不会克隆它的邻居的列表
        Node cloneNode = new Node(node.val, new ArrayList());
        // 哈希表存储
        visited.put(node, cloneNode);
        // 遍历该节点的邻居并更新克隆节点的邻居列表
        for (Node neighbor: node.neighbors) {
            cloneNode.neighbors.add(cloneGraph(neighbor));
        }
        return cloneNode;
    }
    //
    public Node cloneGraphBFS(Node node) {
        if (node == null)  return node;
        HashMap<Node, Node> visited = new HashMap();
        // 将题目给定的节点添加到队列
        LinkedList<Node> queue = new LinkedList<Node> ();
        queue.add(node);
        // 克隆第一个节点并存储到哈希表中
        visited.put(node, new Node(node.val, new ArrayList()));
        // 广度优先搜索
        while (!queue.isEmpty()) {
            // 取出队列的头节点
            Node n = queue.remove();
            // 遍历该节点的邻居
            for (Node neighbor: n.neighbors) {
                if (!visited.containsKey(neighbor)) {
                    // 如果没有被访问过，就克隆并存储在哈希表中
                    visited.put(neighbor, new Node(neighbor.val, new ArrayList()));
                    // 将邻居节点加入队列中
                    queue.add(neighbor);
                }
                // 更新当前节点的邻居列表
                visited.get(n).neighbors.add(visited.get(neighbor));
            }
        }
        return visited.get(node);
    }
}

课程表（mid)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
    //思路:有向图
    List<List<Integer>> edges;
    int[] visited;
    boolean valid = true;
    public boolean canFinish(int numCourses, int[][] prerequisites) {
        edges = new ArrayList<>();
        visited = new int[numCourses];
        for(int i=0;i<numCourses;i++)edges.add(new ArrayList<>());
        for(int[] pre:prerequisites)edges.get(pre[1]).add(pre[0]);
        for(int i=0;i<numCourses&&valid;i++)if(visited[i]==0)dfs(i);
        return valid;
    }
    public void dfs(int index){
        visited[index] = 1;//搜索中
        for(int i:edges.get(index)){
            if(visited[i]==0){
                dfs(i);
                if(!valid)return;
            }else if(visited[i]==1){
                valid = false;
                return;
            }
        }
        visited[index] = 2;//搜索完成
    }
}

课程表 II（mid）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
class Solution {
    // 存储有向图
    List<List<Integer>> edges;
    // 标记每个节点的状态：0=未搜索，1=搜索中，2=已完成
    int[] visited;
    // 用数组来模拟栈，下标 n-1 为栈底，0 为栈顶
    int[] result;
    // 判断有向图中是否有环
    boolean valid = true;
    // 栈下标
    int index;

    public int[] findOrder(int numCourses, int[][] prerequisites) {
        edges = new ArrayList<List<Integer>>();
        for (int i = 0; i < numCourses; ++i) {
            edges.add(new ArrayList<Integer>());
        }
        visited = new int[numCourses];
        result = new int[numCourses];
        index = numCourses - 1;
        for (int[] info : prerequisites) {
            edges.get(info[1]).add(info[0]);
        }
        // 每次挑选一个「未搜索」的节点，开始进行深度优先搜索
        for (int i = 0; i < numCourses && valid; ++i) {
            if (visited[i] == 0) {
                dfs(i);
            }
        }
        if (!valid) {
            return new int[0];
        }
        // 如果没有环，那么就有拓扑排序
        return result;
    }

    public void dfs(int u) {
        // 将节点标记为「搜索中」
        visited[u] = 1;
        // 搜索其相邻节点
        // 只要发现有环，立刻停止搜索
        for (int v: edges.get(u)) {
            // 如果「未搜索」那么搜索相邻节点
            if (visited[v] == 0) {
                dfs(v);
                if (!valid) {
                    return;
                }
            }
            // 如果「搜索中」说明找到了环
            else if (visited[v] == 1) {
                valid = false;
                return;
            }
        }
        // 将节点标记为「已完成」
        visited[u] = 2;
        // 将节点入栈
        result[index--] = u;
    }
}

课程表 III（hard）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    //优先队列排序lastDayi
    public int scheduleCourse(int[][] courses) {
        Arrays.sort(courses, (a, b) -> a[1] - b[1]);
        PriorityQueue<Integer> q = new PriorityQueue<Integer>((a, b) -> b - a);
        // 优先队列中所有课程的总时间
        int total = 0;
        for (int[] course : courses) {
            int ti = course[0], di = course[1];
            if (total + ti <= di) {
                total += ti;
                q.offer(ti);
            } else if (!q.isEmpty() && q.peek() > ti) {
                total -= q.poll() - ti;
                q.offer(ti);
            }
        }
        return q.size();
    }
}

相关资料

https://leetcode-cn.com/leetbook/detail/graph/
https://www.geeksforgeeks.org/breadth-first-search-or-bfs-for-a-graph/

基础算法 > 刷题记录
算法笔记-图论类型
https://mikeygithub.github.io/2020/08/20/yuque/算法笔记-图论类型/
作者
Mikey
发布于
2020年8月20日
许可协议