算法笔记-数组类型

array.png

数组类型

数组类型题目一般可以考虑排序来帮助

相关题目

两数之和

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
    //哈希表
    public int[] twoSum(int[] nums, int target) {
        Map<Integer,Integer> map = new HashMap<>();
        for(int i=0;i<nums.length;i++){
            Integer has = map.get(target-nums[i]);
            if(has!=null) return new int[]{has,i};
            map.put(nums[i],i);
        }
        return new int[0];
    }
}

三数之和

解题思路

排序+指针移动


代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
class Solution {
    public List<List<Integer>> threeSum(int[] nums) {
        int n = nums.length;
        Arrays.sort(nums);
        List<List<Integer>> ans = new ArrayList<List<Integer>>();
        // 枚举 a
        for (int first = 0; first < n; ++first) {
            // 需要和上一次枚举的数不相同
            if (first > 0 && nums[first] == nums[first - 1]) {
                continue;
            }
            // c 对应的指针初始指向数组的最右端
            int third = n - 1;
            int target = -nums[first];
            // 枚举 b
            for (int second = first + 1; second < n; ++second) {
                // 需要和上一次枚举的数不相同
                if (second > first + 1 && nums[second] == nums[second - 1]) {
                    continue;
                }
                // 需要保证 b 的指针在 c 的指针的左侧
                while (second < third && nums[second] + nums[third] > target) {
                    --third;
                }
                // 如果指针重合，随着 b 后续的增加
                // 就不会有满足 a+b+c=0 并且 b<c 的 c 了，可以退出循环
                if (second == third) {
                    break;
                }
                if (nums[second] + nums[third] == target) {
                    List<Integer> list = new ArrayList<Integer>();
                    list.add(nums[first]);
                    list.add(nums[second]);
                    list.add(nums[third]);
                    ans.add(list);
                }
            }
        }
        return ans;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
// 数组遍历首先对数组进行排序，排序后固定一个数 nums[i]，再使用左右指针指向 nums[i]后面的两端，
// 数字分别为 nums[L] 和 nums[R]，计算三个数的和 sum 判断是否满足为 0，满足则添加进结果集
// 如果 nums[i]大于 0，则三数之和必然无法等于 0，结束循环
// 如果 nums[i] == nums[i-1]，则说明该数字重复，会导致结果重复，所以应该跳过
// 当 sum == 0 时，nums[L] == nums[L+1] 则会导致结果重复，应该跳过，L++
// 当 sum == 0 时，nums[R] == nums[R-1] 则会导致结果重复，应该跳过，R--
// 时间复杂度：O(n^2)，n 为数组长度
class Solution {
    public static List<List<Integer>> threeSum(int[] nums) {
        List<List<Integer>> ans = new ArrayList();
        int len = nums.length;
        if(nums == null || len < 3) return ans;
        Arrays.sort(nums); // 排序
        for (int i = 0; i < len ; i++) {
            if(nums[i] > 0) break; // 如果当前数字大于0，则三数之和一定大于0，所以结束循环
            if(i > 0 && nums[i] == nums[i-1]) continue; // 去重
            int L = i+1;
            int R = len-1;
            while(L < R){
                int sum = nums[i] + nums[L] + nums[R];
                if(sum == 0){
                    ans.add(Arrays.asList(nums[i],nums[L],nums[R]));
                    while (L<R && nums[L] == nums[L+1]) L++; // 去重
                    while (L<R && nums[R] == nums[R-1]) R--; // 去重
                    L++;
                    R--;
                }
                else if (sum < 0) L++;
                else if (sum > 0) R--;
            }
        }        
        return ans;
    }
}

四数之和

字符串相加（easy）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
        public String addStrings(String num1, String num2) {
        int length = Math.max(num1.length(),num2.length())+1;
        int[] arr1 = new int[length];
        int[] arr2 = new int[length];
        for (int i = 0,j = num1.length()-1; j >= 0; i++,j--) arr1[i] = num1.charAt(j)-48;
        for (int i = 0,j = num2.length()-1; j >= 0; i++,j--) arr2[i] = num2.charAt(j)-48;
        StringBuilder sb = new StringBuilder();
        int verb = 0;
        for (int i = 0; i < length; i++) {
            int sum = arr1[i] + arr2[i] + verb;
            if (sum>9){
                verb=1;
                sum-=10;
            }else verb=0;
            sb.append(sum);
        }
        sb.reverse();
        if (sb.charAt(0)=='0')sb.deleteCharAt(0);
        return sb.toString();
    }
}

大整数相加（easy）

解题思路： 使用数组存储
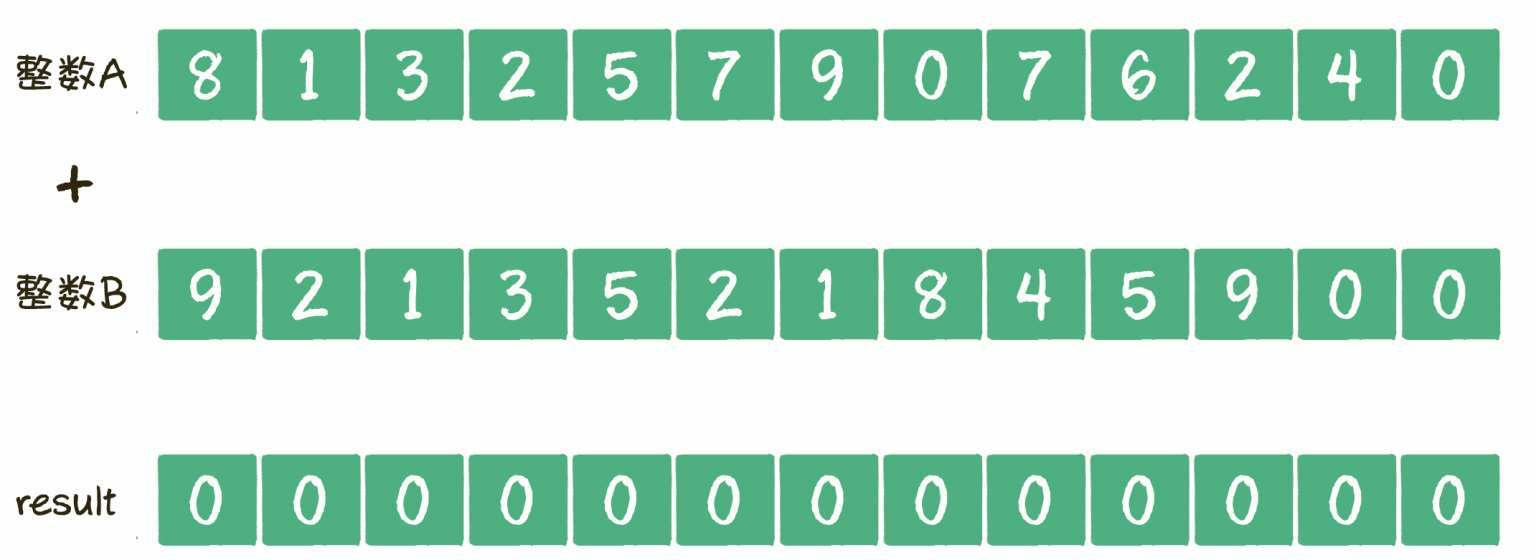
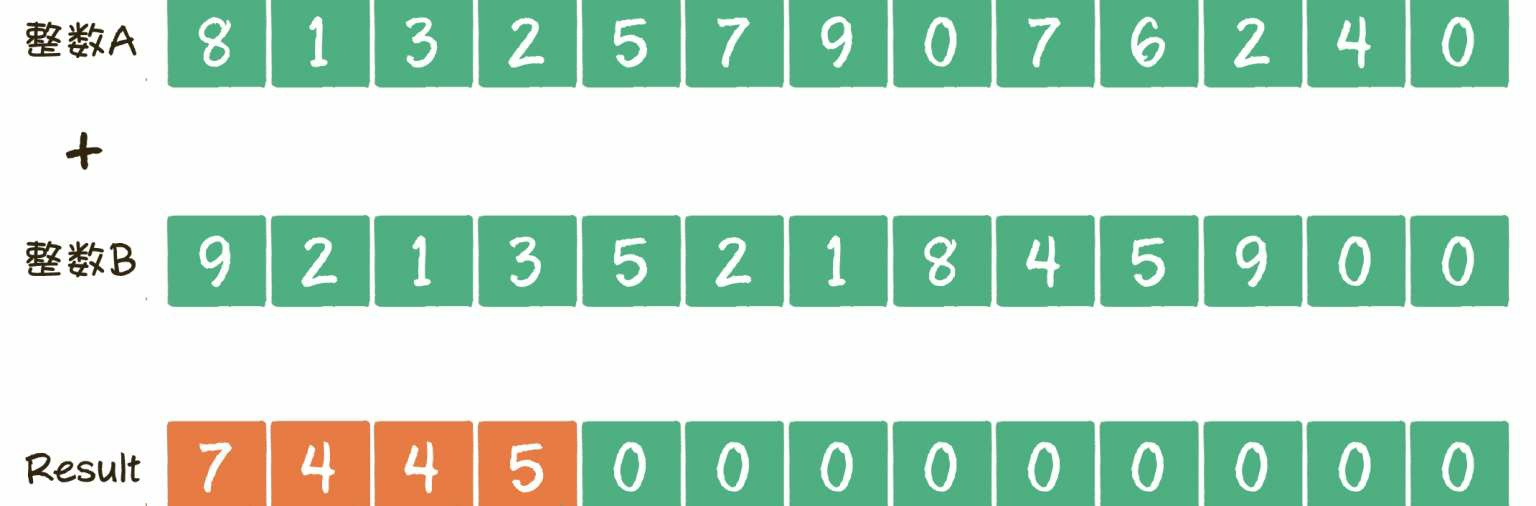
我们以 426 709 752 31 8 + 95481 253 129 为例,来看看大整数相加的详细步骤。
第1步, 创建两个整型数组,数组长度是较大整数的位数+1。把每一个整数倒序存储到数组中,整数的个位存于数组下标为0的位置,最高位存于数组的尾部。之所以倒序存储,是因为这样更符合从左到右访问数组的习惯。

第2步, 创建结果数组,结果数组的长度同样是较大整数的位数+1,+1的目的很明显,是给最高位进位预留的。

第3步, 遍历两个数组,从左到右按照对应下标把元素两两相加,就像小学生计算竖式一样。
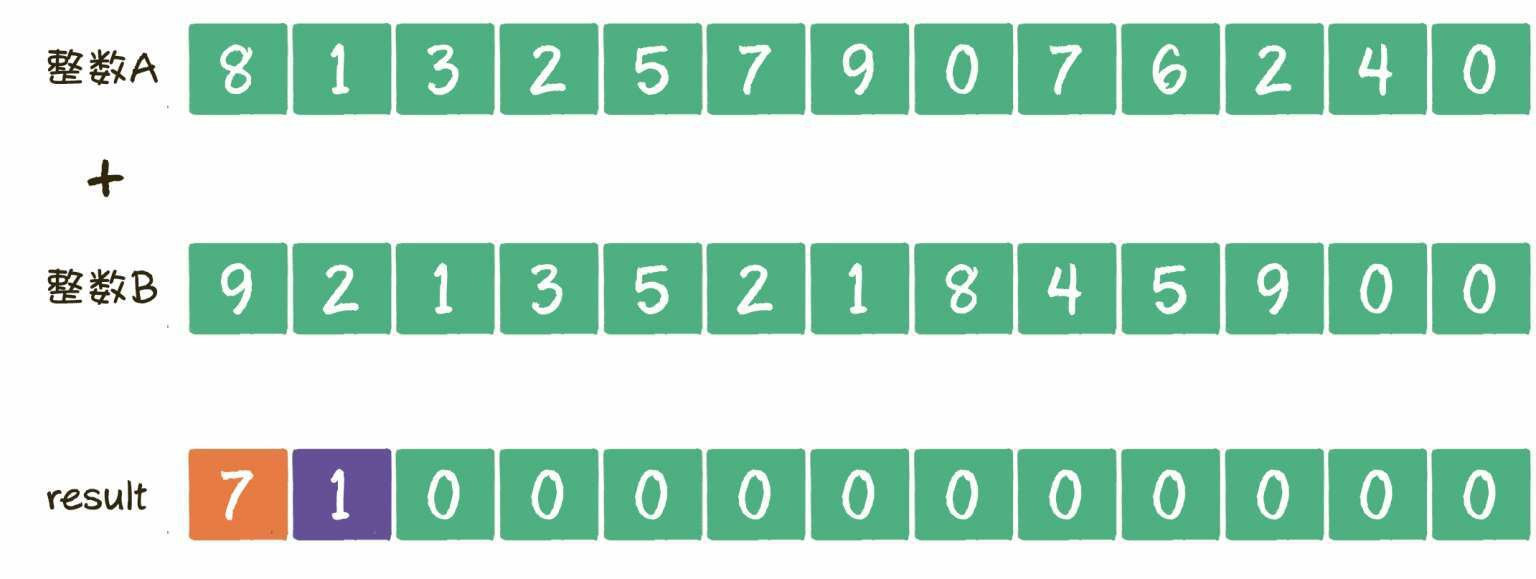
在本示例中,最先相加的是数组A的第1个元素8和数组B的第1个元素9,结果是7,进位1。把7填充到result数组的对应下标位置,进位的1填充到下一个位置。

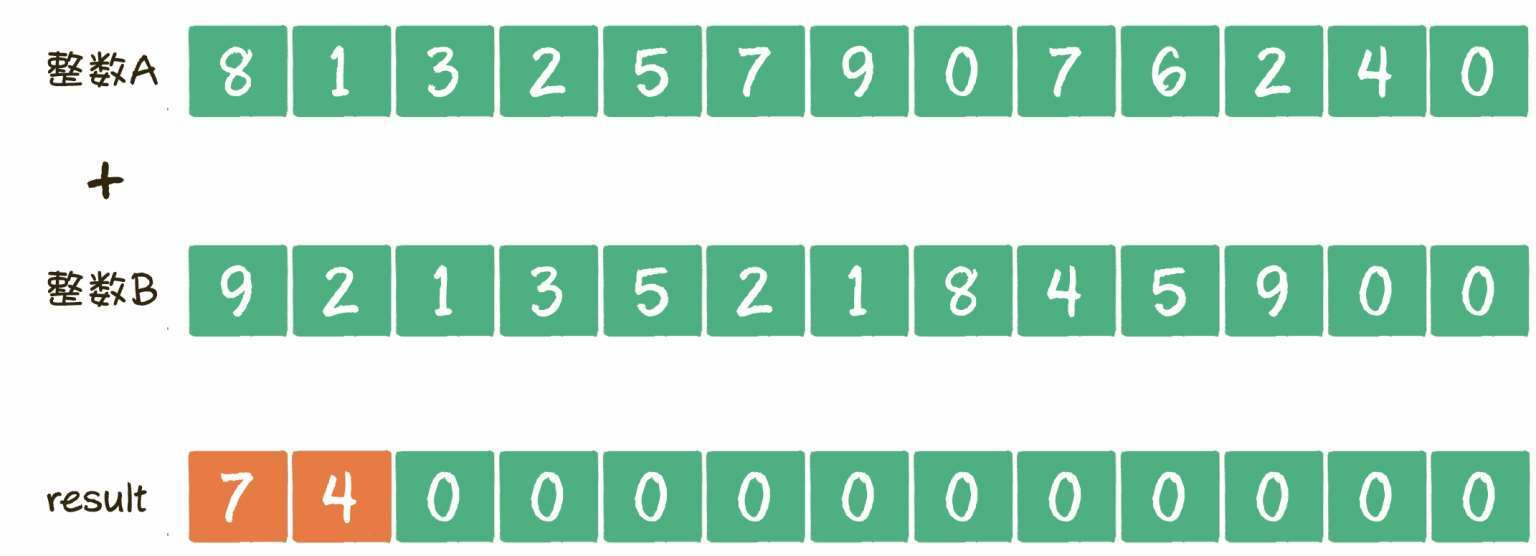
第2组相加的是数组A的第2个元素1和数组B的第2个元素2,结果是3, 再加上刚才的进位1,把4填充到result数组的对应下标位置。

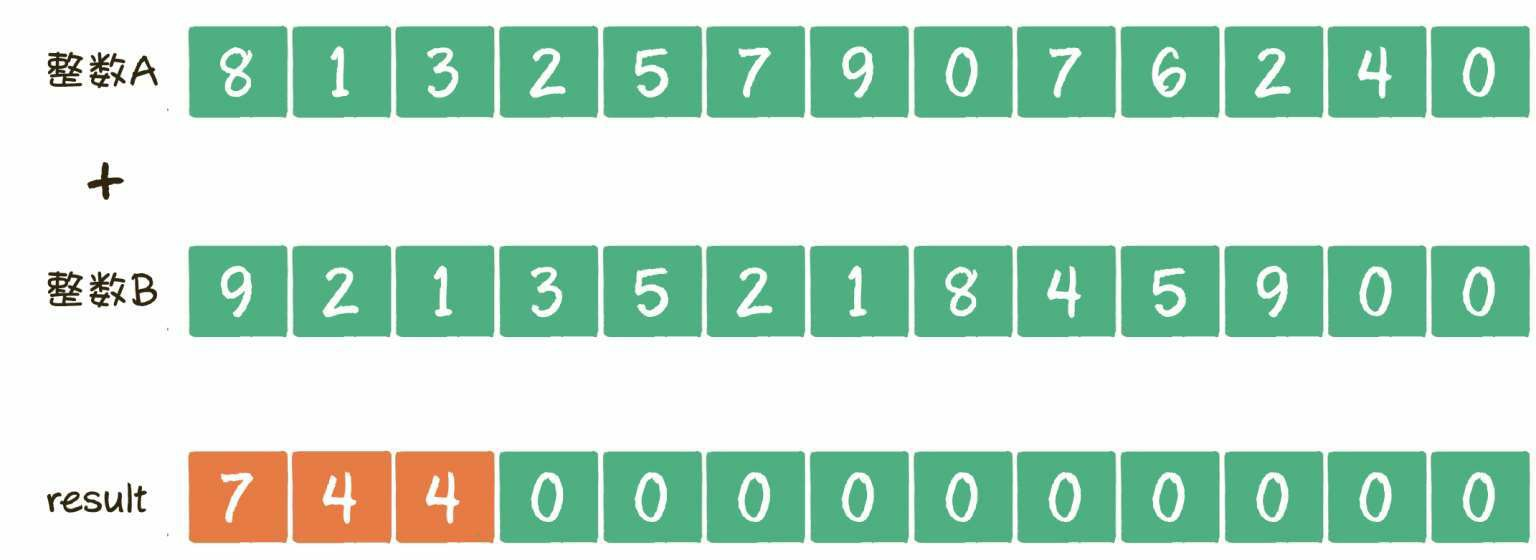
第3组相加的是数组A的第3个元素3和数组B的第3个元素1,结果是4,把4填充到result数组的对应下标位置。

第4组相加的是数组A的第4个元素2和数组B的第4个元素3,结果是5,把5填充到result数组的对应下标位置。

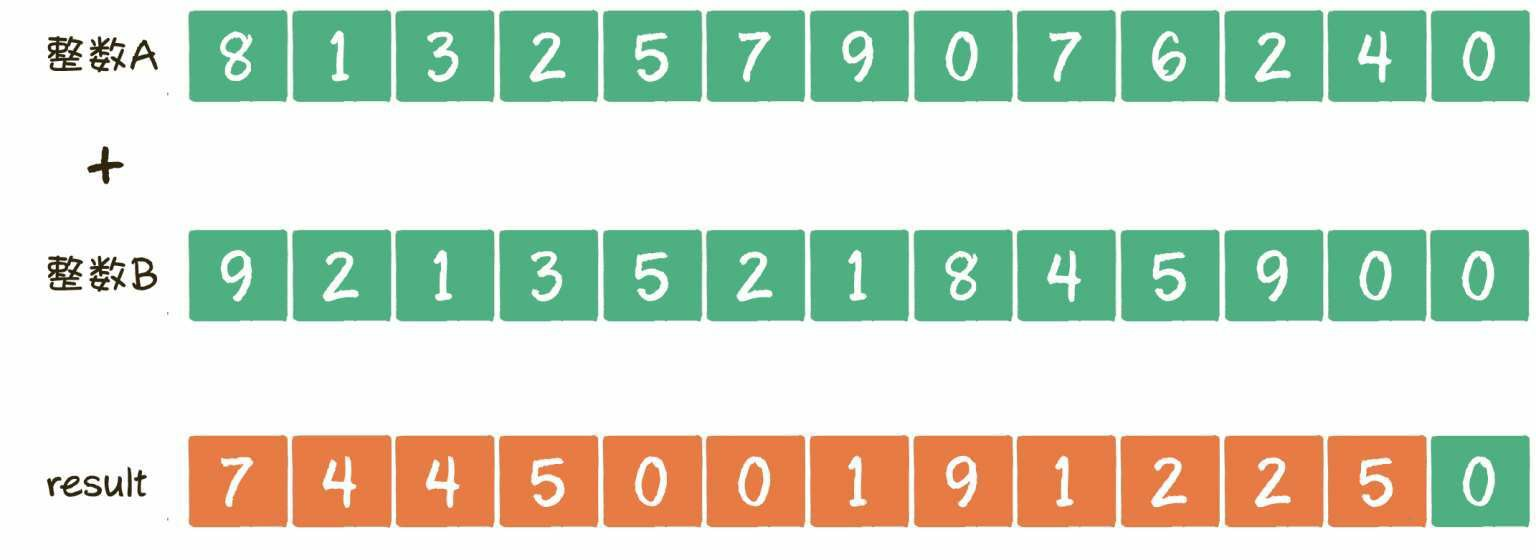
以此类推……一直把数组的所有元素都相加完毕。

第4步, 把result数组的全部元素再次逆序,去掉首位的0,就是最终结果。

需要说明的是,为两个大整数建立临时数组,是一种直观的解决方案。若想节省内存空间,也可以不创建这两个临时数组。
代码实现 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
class Solution {
    public static String bigNumberSum(String bigNumberA, String bigNumberB) {
        //1.把两个大整数用数组逆序存储，数组长度等于较大整数位数+1
        int maxLength = bigNumberA.length() > bigNumberB.length() ? bigNumberA.length() : bigNumberB.length();
        int[] arrayA = new int[maxLength + 1];//+1是为了考虑到进位的问题
        //逆序存储
        for (int i = 0; i < bigNumberA.length(); i++) {
            arrayA[i] = bigNumberA.charAt(bigNumberA.length() - 1 - i) - '0';
        }
        int[] arrayB = new int[maxLength + 1];//+1是为了考虑到进位的问题
        for (int i = 0; i < bigNumberB.length(); i++) {
            arrayB[i] = bigNumberA.charAt(bigNumberB.length() - 1 - i) - '0';
        }
        //2.构建result数组，数组长度等于较大整数位置+1
        int[] result = new int[maxLength + 1];
        //3.遍历数组按位相加
        for (int i = 0; i < result.length; i++) {
            int temp = result[i];
            temp += arrayA[i];
            temp += arrayB[i];
            //判断是否进位
            if (temp > 10) {
                temp = temp - 10;
                result[i + 1] = 1;
            }
            result[i] = temp;
        }
        //4.把数组再次逆序并转为字符串
        StringBuilder sb = new StringBuilder();
        //是否找到大整数的最高有效位
        boolean findFirst = false;
        for (int i = result.length - 1; i >= 0; i--) {
            if (!findFirst) {
                if (result[i] == 0) continue;
                findFirst = true;
            }
            sb.append(result[i]);
        }
        return sb.toString();
    }
}

移动零(简单)

给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。 示例:
输入: [0,1,0,3,12]
输出: [1,3,12,0,0]
说明:
必须在原数组上操作，不能拷贝额外的数组。 尽量减少操作次数。

解题思路

使用双指针，左指针指向当前已经处理好的序列的尾部，右指针指向待处理序列的头部。 右指针不断向右移动，每次右指针指向非零数，则将左右指针对应的数交换，同时左指针右移。 注意到以下性质：

  1. 左指针左边均为非零数；
  2. 右指针左边直到左指针处均为零。 因此每次交换，都是将左指针的零与右指针的非零数交换，且非零数的相对顺序并未改变
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    class Solution {
        public void moveZeroes(int[] nums) {
            int n = nums.length, left = 0, right = 0;
            while (right < n) {
                if (nums[right] != 0) {
                    swap(nums, left, right);
                    left++;
                }
                right++;
            }
        }

        public void swap(int[] nums, int left, int right) {
            int temp = nums[left];
            nums[left] = nums[right];
            nums[right] = temp;
        }
    }

盛最多水的容器(简单)
解题思路

1.采用两层循环，时间复杂度O(n^2)
2.双指针首尾比较,如果比当前的高度小直接跳过比较(过滤),否则进行运算比较

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public class Solution {
    public int maxArea(int[] height) {
        int l = 0, r = height.length - 1;
        int ans = 0;
        while (l < r) {
            int area = Math.min(height[l], height[r]) * (r - l);
            ans = Math.max(ans, area);
            if (height[l] <= height[r]) {
                ++l;
            } else {
                --r;
            }
        }
        return ans;
    }
}

旋转数组(中等)

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
class Solution {
    //暴力破解
    public void rotate(int[] nums, int k) {
        for (int i = k; i > 0; i--) {
            int last = nums[nums.length - 1];
            for (int j = nums.length - 1; j > 0; j--) {
                nums[j] = nums[j - 1];
            }
            nums[0] = last;
        }
    }

    //使用额外的数组
    public void rotate(int[] nums, int k) {
        int[] arr = new int[nums.length];
        for (int i = 0; i < nums.length; i++) {
            arr[(i + k) % nums.length] = nums[i];
        }
        for (int i = 0; i < nums.length; i++) nums[i] = arr[i];
    }

    //反转
    public void rotate(int[] nums, int k) {
        k %= nums.length;
        reverse(nums, 0, nums.length - 1);
        reverse(nums, 0, k - 1);
        reverse(nums, k, nums.length - 1);
    }

    //反转
    public void reverse(int[] nums, int start, int end) {
        while (start < end) {
            int temp = nums[start];
            nums[start] = nums[end];
            nums[end] = temp;
            start++;
            end--;
        }
    }
    //TODO:使用环状替换
}

旋转图像

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class Solution {
    //[5,1,9,11]
    //[2,4,8,10]
    //[13,3,6,7]
    //[5,4,1,16]
    //每次旋转四个点，由外向里
    public void rotate(int[][] matrix) {
        int n = matrix.length; 
        for (int i = 0; i < n / 2; ++i) { 
            for (int j = 0; j < (n + 1) / 2; ++j) { 
                int temp = matrix[i][j]; 
                matrix[i][j] = matrix[n - j - 1][i]; 
                matrix[n - j - 1][i] = matrix[n - i - 1][n - j - 1]; 
                matrix[n - i - 1][n - j - 1] = matrix[j][n - i - 1]; 
                matrix[j][n - i - 1] = temp; 
            }
        }
    }
    //对称
    public void rotate(int[][] matrix) {
        int n = matrix.length;
        //先沿斜对角线翻转
        for(int i = 0;i < n;i ++)
            for(int j = 0;j < i;j ++){
                int temp = matrix[i][j];
                matrix[i][j] = matrix[j][i];
                matrix[j][i] = temp;
       }
       //再沿垂直竖线翻转
       for(int i = 0;i < n;i ++)
            for(int j = 0, k = n - 1; j < k ; j++, k--){
                int temp = matrix[i][k];
                matrix[i][k] = matrix[i][j];
                matrix[i][j] = temp;
        }
    }
}

加一(简单)

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
    public int[] plusOne(int[] digits) {
        for (int i = digits.length - 1; i >= 0; i--) {
            digits[i]++;
            digits[i] = digits[i] % 10;
            if (digits[i] != 0) return digits;
        }
        digits = new int[digits.length + 1];
        digits[0] = 1;
        return digits;
    }
}

删除排序数组中的重复项（easy)

方法：双指针法

数组完成排序后，我们可以放置两个指针 i 和 j，其中 i 是慢指针，而 j 是快指针。只要 nums[i] = nums[j]，我们就增加 j 以跳过重复项。
当我们遇到 nums[j]!=nums[i] 时，跳过重复项的运行已经结束，因此我们必须把它（nums[j]）的值复制到 nums[i+1]。然后递增 i，接着我们将再次重复相同的过程，直到 j 到达数组的末尾为止。

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
    public int removeDuplicates(int[] nums) {
        if (nums.length == 0) return 0;
        int i = 0;
        for (int j = 1; j < nums.length; j++) {
            if (nums[j] != nums[i]) {
                i++;
                nums[i] = nums[j];
            }
        }
        return i + 1;
    }
}

复杂度分析
时间复杂度：O(n)，假设数组的长度是 n，那么 i 和 j 分别最多遍历 n 步。
空间复杂度：O(1)。

柱状图中最大的矩形(困难)

题目描述

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。求在该柱状图中，能够勾勒出来的矩形的最大面积。

解题思路

代码实现

根据身高重建队列(中等)

https://leetcode-cn.com/problems/queue-reconstruction-by-height/

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
思路：对数组进行降序排序，身高高在前面，在对比进行插入
class Solution {
 	public int[][] reconstructQueue(int[][] people) {
        if (0 == people.length || 0 == people[0].length)return new int[0][0];
         //按照身高降序 K升序排序 
        Arrays.sort(people, new Comparator<int[]>() {
            @Override
            public int compare(int[] o1, int[] o2) {
                return o1[0] == o2[0] ? o1[1] - o2[1] : o2[0] - o1[0];
            }
        });
        List<int[]> list = new ArrayList<>();
        //K值定义为 排在h前面且身高大于或等于h的人数 
        //因为从身高降序开始插入，此时所有人身高都大于等于h
        //因此K值即为需要插入的位置
        for (int[] i : people) {
            list.add(i[1], i);//在i[i]位置插入，后面元素后移
        }
        return list.toArray(new int[list.size()][]);

    }
}

合并两个有序数组（easy）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
    //思路：类似合并链表，两个指针记录两个数组移动的位置，另一个指针记录新数组下标
    public void merge(int[] nums1, int m, int[] nums2, int n) {
        int[] ans = new int[m+n];
        int i1 = 0,i2 = 0,i3 = 0;
        while(i1<m&&i2<n){
            if(nums1[i1]<nums2[i2]){
                ans[i3]=nums1[i1];
                i1++;
            }else{
                ans[i3]=nums2[i2];
                i2++;
            }
            i3++;
        }
        //拼接剩余
        if(i1==m){
            for(int i=i2;i<n;i++){
                ans[i3]=nums2[i];
                i3++;
            }
        }else if(i2==n){
            for(int i=i1;i<m;i++){
                ans[i3]=nums1[i];
                i3++;
            }
        }
        for(int i=0;i<ans.length;i++)nums1[i]=ans[i];
    }
}

合并区间

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    public int[][] merge0(int[][] intervals) {
        if (intervals.length == 0) {
            return new int[0][2];
        }
        //排序
        Arrays.sort(intervals, new Comparator<int[]>() {
            public int compare(int[] interval1, int[] interval2) {
                return interval1[0] - interval2[0];
            }
        });
        List<int[]> merged = new ArrayList<int[]>();
        for (int i = 0; i < intervals.length; ++i) {
            int L = intervals[i][0], R = intervals[i][1];
            //没有重叠
            if (merged.size() == 0 || merged.get(merged.size() - 1)[1] < L) {
                merged.add(new int[]{L, R});
            } else {
                merged.get(merged.size() - 1)[1] = Math.max(merged.get(merged.size() - 1)[1], R);
            }
        }
        return merged.toArray(new int[merged.size()][]);
    }
}

螺旋矩阵

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
    public List<Integer> spiralOrder(int[][] matrix) {
        List<Integer> order = new ArrayList<Integer>();
        if (matrix == null || matrix.length == 0 || matrix[0].length == 0) return order;
        int rows = matrix.length, columns = matrix[0].length;
        //控制四个角的下标
        int left = 0, right = columns - 1, top = 0, bottom = rows - 1;
        //控制条件
        while (left <= right && top <= bottom) {
            //上
            for (int column = left; column <= right; column++) order.add(matrix[top][column]);
            //右
            for (int row = top + 1; row <= bottom; row++) order.add(matrix[row][right]);
            //需要再次判断控制条件
            if (left < right && top < bottom) {
                //下
                for (int column = right - 1; column > left; column--) order.add(matrix[bottom][column]);
                //左
                for (int row = bottom; row > top; row--)order.add(matrix[row][left]);
            }
            //集体缩小一圈
            left++;
            right--;
            top++;
            bottom--;
        }
        return order;
    }
}

螺旋矩阵II

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    //思路:四个变量控制上下左右
    public int[][] generateMatrix(int n) {
        int[][] arr = new int[n][n];
        int left = 0,right = n-1,up = 0,down = n-1,num = 0;
        while(left<=right||up<down){
            for(int i=left;i<=right;i++)arr[up][i] = ++num;
            up++;
            for(int i=up;i<=down;i++)arr[i][right] = ++num;
            right--;
            for(int i=right;i>=left;i--)arr[down][i] = ++num;
            down--;
            for(int i=down;i>=up;i--)arr[i][left] = ++num;
            left++;
        }
        return arr;
    }
}

接雨水

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
    //按列进行遍历，相两边扩散查找最高点left_max,right_max，取Math.min(left_max,right_max)，得max-i
    public int trapbf(int[] height){
        int ans = 0;
        for(int i=0;i<height.length;i++){
            int leftMax = 0;
            int rightMax = 0;
            //get left max
            for(int l=i-1;l>=0;l--)leftMax=Math.max(leftMax,height[l]);
            //get right max
            for(int r=i+1;r<height.length;r++)rightMax=Math.max(rightMax,height[r]);
            //cal area
            int min = Math.min(leftMax,rightMax);
            int area = Math.max(0,min - height[i]);
            ans+=area;
        }
        return ans;
    }
    //基于bf其重复的过程是每次都有向两边扩散去查找最大值，那么我们可以提前把每个height[i]先求出来再，遍历
    public int trap(int[] height) {
        //左边最大值
        int[] leftMax = new int[height.length];
        leftMax[0] = height[0];
        for (int i = 1; i < height.length; i++) leftMax[i] = Math.max(leftMax[i-1],height[i]);
        //右边最大值
        int[] rightMax = new int[height.length];
        rightMax[rightMax.length-1] = height[height.length-1];
        for (int i = rightMax.length-2; i >= 0; i--)rightMax[i] = Math.max(rightMax[i+1],height[i]);
        //计算结果
        int ans = 0;
        for (int i = 0; i < height.length; i++)ans+=Math.min(leftMax[i],rightMax[i])-height[i];
        return ans;
    }
}

下一个排列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
//思路：从后往前找出现num[i]<num[i+1]的数，在[i+1,nums.length]中查出比num[i]大的最接近的数交换
public void nextPermutation(int[] nums) {
    for (int i = nums.length-1; i > 0; i--) {
        //当出现num[i]<num[i+1]时,需要从i+1~nums.length找出大于num[i]的最接近的数交换
        if (nums[i]>nums[i-1]){
            int index = i;
            for (int j = i; j < nums.length ; j++) {
                if (nums[j]>nums[i-1]&&nums[j]-nums[i-1]<nums[index]-nums[i-1])index=j;
            }
            int temp = nums[i-1];
            nums[i-1] = nums[index];
            nums[index] = temp;
            Arrays.sort(nums,i,nums.length);
            return;
        }
    }
    Arrays.sort(nums);
}

缺失的第一个正数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
    //通过:数组的元素和元素位置构建一个数组哈希表。遍历数组，将当前出现元素值，映射到下标，将其值设置为负数(打标记)
    //如: nums=[1,4,7,2,5] 遍历到 nums[2]时将下标为3的数设置为-7,标记2出现过。
    //
    //具体：
    //我们将数组中所有小于等于 0 的数修改为 N+1；
	//我们遍历数组中的每一个数 x，它可能已经被打了标记，因此原本对应的数为 ∣x∣，其中 ∣∣ 为绝对值符号。如果 ∣x∣∈[1,N]，那么我们给数组中的第 ∣x∣−1 个位置的数添加一个负号。注意如果它已经有负号，不需要重复添加；
	//在遍历完成之后，如果数组中的每一个数都是负数，那么答案是 N+1，否则答案是第一个正数的位置加 1。
    public int firstMissingPositive(int[] nums) {
        int n = nums.length;
        for (int i = 0; i < n; ++i) {
            if (nums[i] <= 0) {
                nums[i] = n + 1;
            }
        }
        for (int i = 0; i < n; ++i) {
            int num = Math.abs(nums[i]);
            if (num <= n) {
                nums[num - 1] = -Math.abs(nums[num - 1]);
            }
        }
        for (int i = 0; i < n; ++i) {
            if (nums[i] > 0) {
                return i + 1;
            }
        }
        return n + 1;
    }
}

最小时间差

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
class Solution {
    //思路:转换成分钟求差值排序
    //算出每个事件差值进行比较，时间复杂度O(n^2)
    public int findMinDifference(List<String> timePoints) {
        int len = timePoints.size();
        if (len > 1440) return 0;
        int[] times = new int[timePoints.size()];
        for(int i=0;i<len;i++){
            String t1 = timePoints.get(i);
            int t1_h = Integer.valueOf(t1.substring(0,2));
            int t1_m = Integer.valueOf(t1.substring(3,5));
            times[i] = t1_h * 60 + t1_m;
        }
        Arrays.sort(times);
        int min = times[0]+1440-times[len-1];
        for(int i=1;i<len;i++){
            min = Math.min(min,times[i]-times[i-1]);
        }
        return min;
    }
    //鸽巢原理
    //根据题意，一共有 24×60=1440 种不同的时间。由鸽巢原理可知，如果 timePoints 长度超过 1440，那必然会有两个相同的时间，此时可直接返回 0
    public int findMinDifference0(List<String> timePoints) {
        int n = timePoints.size();
        if (n > 1440) return 0;
        Collections.sort(timePoints);
        int ans = Integer.MAX_VALUE;
        int t0Minutes = getMinutes(timePoints.get(0));
        int preMinutes = t0Minutes;
        for (int i = 1; i < n; ++i) {
            int minutes = getMinutes(timePoints.get(i));
            ans = Math.min(ans, minutes - preMinutes); // 相邻时间的时间差
            preMinutes = minutes;
        }
        ans = Math.min(ans, t0Minutes + 1440 - preMinutes); // 首尾时间的时间差
        return ans;
    }
    public int getMinutes(String t) {
        return ((t.charAt(0) - '0') * 10 + (t.charAt(1) - '0')) * 60 + (t.charAt(3) - '0') * 10 + (t.charAt(4) - '0');
    }
}

搜索二维矩阵

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
//二分查找
    public boolean searchMatrix(int[][] matrix, int target) {
        int m = matrix.length;
        int n = matrix[0].length;
        int left = 0,right = (m*n)-1;
        int pivotIdx = 0, pivotElement = 0;
        while(left<=right){
            pivotIdx = (left+right)/2;
            pivotElement = matrix[pivotIdx/n][pivotIdx%n];
            if(target==pivotElement)return true;
            else{
                if(target<pivotElement)right=pivotIdx-1;
                else left = pivotIdx + 1;
            }
        }
        return false;
    }

搜索二维矩阵 II

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
class Solution {
    //思路：
    //1.若左下角元素等于目标，则找到
    //2.若左下角元素大于目标，则目标不可能存在于当前矩阵的最后一行，问题规模可以减小为在去掉最后一行的子矩阵中寻找目标
    //3.若左下角元素小于目标，则目标不可能存在于当前矩阵的第一列，问题规模可以减小为在去掉第一列的子矩阵中寻找目标
    //4.若最后矩阵减小为空，则说明不存在 
    public boolean searchMatrix(int[][] matrix, int target) {
        int x=matrix.length-1,y=0;
        while(x>=0&&y<matrix[0].length){
            if(matrix[x][y]==target) return true;
            if(matrix[x][y]>target) x--;//当大于target则开启另一个列查找
            else y++;
        }
        return false;
    }
}
class Solution {

    //[1,4,7,11,15],
    //[2,5,8,12,19],
    //[3,6,9,16,22],
    //[10,13,14,17,24],
    //[18,21,23,26,30]]
    
    //根据定义可知同一行左边小于右边，同一列上边小于下边。

    // 1.右上角大于同一行左边的所有数，小于同一列下边的所有数，其位于中间可以定位target在哪一边，
    // 如果右上角大于target，因为该列从上到下递增(下面所有的数都大于target)，所以target必不肯能在该列，排除该列，y--向前一列继续查找
    // 如果右上角小于target，因为该行从左到右递增(左边所有的数都小于target)，所以target必不肯能在该行，排除该行，x++向下一行继续查找
    // （左下角同理）

    // 2.左上角和右下角分别都小于和大于所有的数，无法确定其区间

    //方法1从右上角开始查询:
    // 从二维数组的右上角开始查找。如果当前元素等于目标值，则返回 true。
    // 如果当前元素大于目标值，则移到左边一列。
    // 如果当前元素小于目标值，则移到下边一行。
    
    //方法2从左下角开始查询:
    // 从二维数组的左下角开始查找。如果当前元素等于目标值，则返回 true。
    // 如果当前元素大于目标值，则移到上边一行。
    // 如果当前元素小于目标值，则移到右边一列。
    public boolean findNumberIn2DArray(int[][] matrix, int target) {
        //方法1
        if(matrix==null||matrix.length==0||matrix[0].length==0)return false;
        int m = matrix.length;
        int n = matrix[0].length;
        int x = 0,y = n - 1;
        while (x<m&&y>=0){
            if (matrix[x][y]==target)return true;
            else if(matrix[x][y]>target)y--;
            else x++;
        }
        return false;
        //方法2
        if(matrix==null||matrix.length==0||matrix[0].length==0)return false;
        int m = matrix.length;
        int n = matrix[0].length;
        int x = m-1,y = 0;
        while (y<n&&x>=0){
            if (matrix[x][y]==target)return true;
            else if(matrix[x][y]>target)x--;
            else y++;
        }
        return false;
    }
}

岛屿的最大面积

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
    //思路：bfs
    private int max;
    private int area;
    public int maxAreaOfIsland(int[][] grid) {
        int m = grid.length;
        int n = grid[0].length;
        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){
                if(grid[i][j]==1){
                    area=0;
                    bfs(grid,i,j);
                    max=Math.max(max,area);
                }
            }
        }
        return max;
    }
    public void bfs(int[][] grid,int x,int y){
        area+=1;
        grid[x][y]=0;
        //上
        if(x>0&&grid[x-1][y]==1)bfs(grid,x-1,y);
        //下
        if(x<grid.length-1&&grid[x+1][y]==1)bfs(grid,x+1,y);
        //左
        if(y>0&&grid[x][y-1]==1)bfs(grid,x,y-1);
        //右
        if(y<grid[0].length-1&&grid[x][y+1]==1)bfs(grid,x,y+1);
    }
}

最大数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    //思路:排序。按照每个数位比较，优先使用位大的
    public String largestNumber(int[] nums) {
        StringBuilder sb = new StringBuilder();
        String[] arr = new String[nums.length];
        for(int i=0;i<arr.length;i++)arr[i]=String.valueOf(nums[i]);
        Arrays.sort(arr, new Comparator<String>() {
           @Override
           public int compare(String o1, String o2) {
               //继承此方法的时候，要自定义比较器，conpareTo方法返回值为1(升序),0，-1(降序)。返回正值 交换；负值不交换
               return (o2 + o1).compareTo((o1 + o2));
           }
        });
        for(String s:arr)sb.append(s);
        String ans = sb.toString();
        if(ans.charAt(0)=='0')ans = "0";
        return ans;
    }
}

对角线遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
class Solution {
    public int[] findDiagonalOrder(int[][] mat) {
        int m = mat.length;
        int n = mat[0].length;
        int t = m+n-1;
        int[] ans = new int[m*n];
        for (int i = 0,x = 0,y = 0,index=0; i < t; i++) {
            //遍历一轮
            while (x>=0&&x<m&&y>=0&&y<n){
                if (i%2==0) {//上
                    ans[index++]=mat[x][y];
                    x--;
                    y++;
                }else {//下
                    ans[index++]=mat[x][y];
                    x++;
                    y--;
                }
            }
            if (i%2==0){//上
                if (x<0&&y==n){
                    x+=2;
                    y--;
                }
                else if (x<0)x++;//归位
                else if (y==n){
                    x+=2;
                    y--;
                }
            }else {
                if (y<0&&x==m){
                    y+=2;
                    x--;
                }
                else if (y<0)y++;//归位
                else if (x==m){
                    y+=2;
                    x--;
                }
            }
        }
        return ans;
    }
}

移动零（easy）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    //双指针p1指向
    //[0,1,0,3,12]
    //[1,1,0,3,12]
    //[1,3,0,3,12]
    //[1,3,12,3,12]
    //[1,3,12,0,0]
    public void moveZeroes(int[] nums) {
        int p1 = 0,p2 = 0;
        while(p2<nums.length){
            if(nums[p2]!=0){
                nums[p1++] = nums[p2];
            }
            p2++;
        }
        //p1后面全部置0
        while(p1<nums.length)nums[p1++]=0;
    }
}

调整数组顺序使奇数位于偶数前面（easy）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    //双指针,首尾遍历(首寻找偶数，尾寻找奇数，交换位置)
    public int[] exchange(int[] nums) {
        int left = 0,right = nums.length-1;
        while(left<right){
            while(left<right&&(nums[left]&1)==1)left++;
            while(right>0&&(nums[right]&1)==0)right--;
            if(left<right){
                int l = nums[left];
                nums[left] = nums[right];
                nums[right] = l;
            }
            left++;
            right--;
        }
        return nums;
    }
}

游戏中弱角色的数量

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
//properties[i] = [attack, defense]
//思路：排序+比较
public int numberOfWeakCharacters0(int[][] properties) {
    Arrays.sort(properties, (o1, o2) -> {
        return o1[0] == o2[0] ? (o1[1] - o2[1]) : (o2[0] - o1[0]);//properties[attack, defense]对attack降序defense升序排序
    });
    int maxDef = 0;
    int ans = 0;
    //此时properties已经排序好，只需要比较每个properties的defense是否小于maxDef，小于更新ans，不小于则更新maxDef
    for (int[] p : properties) {
        if (p[1] < maxDef) {
            ans++;
        } else {
            maxDef = p[1];
        }
    }
    return ans;
}
//单调栈
public int numberOfWeakCharacters(int[][] properties) {
    Arrays.sort(properties, (o1, o2) -> {
        return o1[0] == o2[0] ? (o2[1] - o1[1]) : (o1[0] - o2[0]);//properties[attack, defense]对attack升序defense降序排序
    });
    int ans = 0;
    Deque<Integer> st = new ArrayDeque<Integer>();
    //此时properties中的attack从小到大,attack相等defense小的在后面
    //遍历数组properties，栈顶小于当前properties[i]将其弹栈，否则压栈
    for (int[] p : properties) {
        while (!st.isEmpty() && st.peek() < p[1]) {
            st.pop();
            ans++;
        }
        st.push(p[1]);
    }
    return ans;
}

和为 K 的子数组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
    //注意题目要求的是连续的子数组，所以可以通过暴力直接滑动求
    public int subarraySum0(int[] nums, int k) {
        int n = nums.length;
        int ans = 0;
        for(int start = 0;start<n;start++){
            int sum = 0;
            for(int end = start;end>=0;end--){
                sum+=nums[end];
                if(sum==k)ans++;
            }
        }
        return ans;
    }
    //前缀和优化，map存储从0-i的数和，当我们需要求连续数组和为k的值时，只需要判断num[i]-k的前缀和是否存在即可
    //以map来存储前缀和为键，次数为值
    public int subarraySum(int[] nums, int k) {
        int count = 0, pre = 0;
        HashMap < Integer, Integer > mp = new HashMap < > ();
        mp.put(0, 1);
        for (int i = 0; i < nums.length; i++) {
            pre += nums[i];
            if (mp.containsKey(pre - k)) {//判断是否存在前缀和为pre-k的值
                count += mp.get(pre - k);
            }
            mp.put(pre, mp.getOrDefault(pre, 0) + 1);
        }
        return count;
    }
}

打乱数组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
class Solution {
    private int[] nums;
    private int[] origin;
    public Solution(int[] nums) {
        this.nums = nums;
        int[] origin = new int[nums.length];
        System.arraycopy(nums,0,origin,0,nums.length);
        this.origin = origin;
    }
    public int[] reset() {
        return origin;
    }
    //bf
    public int[] shuffle1() {
        List<Integer> list = new ArrayList<>();
        int[] shuffle = new int[nums.length];
        for(int n:origin)list.add(n);
        Random random = new Random();
        //每次在list里随机获取一个数来填充shuffle
        for(int i=0;i<nums.length;i++){
            int r = random.nextInt(list.size());
            shuffle[i] = list.remove(r);
        }
        return shuffle;
    }
    //Fisher-Yates 洗牌算法
    //将当前nums[i]元素与nums(i,n)随机元素交换位置，减少了创建list的开销
    public int[] shuffle() {
        Random random = new Random();
        for(int i=0;i<nums.length;i++){
            int index = i+random.nextInt(nums.length-i);
            int tmp = nums[i];
            nums[i] = nums[index];
            nums[index] = tmp;
        }
        return nums;
    }
}

两个数组的交集

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
class Solution {
    //set
    public int[] intersectionSet(int[] nums1, int[] nums2) {
        List<Integer> list = new ArrayList<>();
        Set<Integer> set1 = new HashSet<>();
        Set<Integer> set2 = new HashSet<>();
        for(int n:nums1)set1.add(n);
        for(int n:nums2)set2.add(n);
        for(int n:set1){
            if (set2.contains(n)){
                list.add(n);
            }
        }
        int[] ret = new int[list.size()];
        for (int i = 0; i < list.size(); i++) ret[i] = list.get(i);
        return ret;
    }
    //排序+双指针
    //[4,5,9]
    //[4,4,8,9,9] 
    public int[] intersection(int[] nums1, int[] nums2) {
        Arrays.sort(nums1);
        Arrays.sort(nums2);
        int m = nums1.length;
        int n = nums2.length;
        int[] intersection = new int[m+n];
        int index = 0,index1 = 0,index2 = 0;
        while(index1<m&&index2<n){
            int n1 = nums1[index1];
            int n2 = nums2[index2];
            if(n1==n2){
                //判断是否重复
                if(index==0||n1!=intersection[index-1])intersection[index++]=n1;
                index1++;
                index2++;
            }else if(n1<n2){
                index1++;
            }else{
                index2++;
            }
        }
        return Arrays.copyOfRange(intersection,0,index);
    }
}

和为 K 的最少斐波那契数字数目

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    public int findMinFibonacciNumbers(int k) {
        //求出斐波拉契数列
        List<Integer> f = new ArrayList<Integer>();
        f.add(1);
        int a = 1, b = 1;
        while (a + b <= k) {
            int c = a + b;
            f.add(c);
            a = b;
            b = c;
        }
        //由题目已知，数据保证对于给定的 k ，一定能找到可行解，所以可以从后往前查找
        int ans = 0;
        for (int i = f.size() - 1; i >= 0 && k > 0; i--) {
            int num = f.get(i);
            if (k >= num) {
                k -= num;
                ans++;
            }
        }
        return ans;
    }
}

顺时针打印矩阵(easy)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
    //[1,2,3,4],
    //[5,6,7,8],
    //[9,10,11,12]
    //思路：四个变量控制边界
    public int[] spiralOrder(int[][] matrix) {
        int m = matrix.length;
        if(matrix==null||m==0)return new int[0];
        int n = matrix[0].length;
        if(n==0)return new int[0];
        int retLen = m * n;
        int[] ret = new int[retLen];
        int index = 0;
        int left = 0,right = n - 1,up = 0,down = m - 1;
        while(left<=right&&up<=down){
            for(int i=left;i<=right;i++)ret[index++]=matrix[up][i];//右边
            for(int i=up+1;i<=down;i++)ret[index++]=matrix[i][right];//下
            if(up<down&&left<right){
                for(int i=right-1;i>left;i--)ret[index++]=matrix[down][i];//左
                for(int i=down;i>up;i--)ret[index++]=matrix[i][left];//上
            }
            up++;
            right--;
            down--;
            left++;
        }
        return ret;
    }
}

数组中重复的数据

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    //原地hash:对数组每个元素所映射的下标都加N,在遍历数组进行判断是否大于N,对N取模得出原来的数
    public List<Integer> findDuplicates(int[] nums) {
        List<Integer> ret = new ArrayList<>();
        int N = 1000000;
        for(int i=0;i<nums.length;i++){
            if(nums[nums[i]%N-1]<N){
                nums[nums[i]%N-1]+=N;
            }else{
                ret.add(nums[i]%N);
            }
        }
        return ret;
    }
}

954. 二倍数对数组（mid）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
    //条件：1. 0<=i <len(arr)/2  2. arr[2 * i + 1] = 2 * arr[2 * i]
    //考查：数组中是否存在n/2对数,每对元素中一个数是另一个数的两倍,可能涉及的数据结构：排序、哈希表
    //思路：map统计每个数出现的频率,对出现的数进行绝对值排序(因为要优先使用小的数来匹配,由于2*负数=更小的负数,更小的负数排序后会在后面),遍历查看是否都匹配
    //边界：和0匹配的值只能是0
    public boolean canReorderDoubled(int[] arr) {
        int n = arr.length;
        Map<Integer,Integer> map = new HashMap<>(300);
        for(int num:arr){
            map.put(num,map.getOrDefault(num,0)+1);
        }
        if(map.getOrDefault(0,0)%2!=0)return false;
        List<Integer> values = new ArrayList<>(map.size());
        for(Integer key:map.keySet())values.add(key);
        //排序前:7,2,-2,-3,5,6
        //排序后:2,-2,-3,5,6,7
        Collections.sort(values,(x,y)->Math.abs(x)-Math.abs(y));
        for (int num:values) {
            int key = 2*num;
            int c2 = map.getOrDefault(key,0);
            int c1 = map.get(num);
            if(c2<c1)return false;
            map.put(key,c2-c1);
        }
        return true;
    }
}

相关资料

基础算法 > 刷题记录
算法笔记-数组类型
https://mikeygithub.github.io/2020/04/26/yuque/算法笔记-数组类型/
作者
Mikey
发布于
2020年4月26日
许可协议