
回溯算法
回溯算法实际上一个类似枚举的搜索尝试过程,主要是在搜索尝试过程中寻找问题的解,当发现已不满足求解条件时,就“回溯”返回,尝试别的路径。回溯法是一种选优搜索法,按选优条件向前搜索,以达到目标。但当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择,这种走不通就退回再走的技术为回溯法,而满足回溯条件的某个状态的点称为“回溯点”。许多复杂的,规模较大的问题都可以使用回溯法,有“通用解题方法”的美称。
一般来说,对其数组进行回溯后可得出的数据,如下[1,2,3,4]全排列,可视化后得出回溯树,可根据图像进行理解记忆。
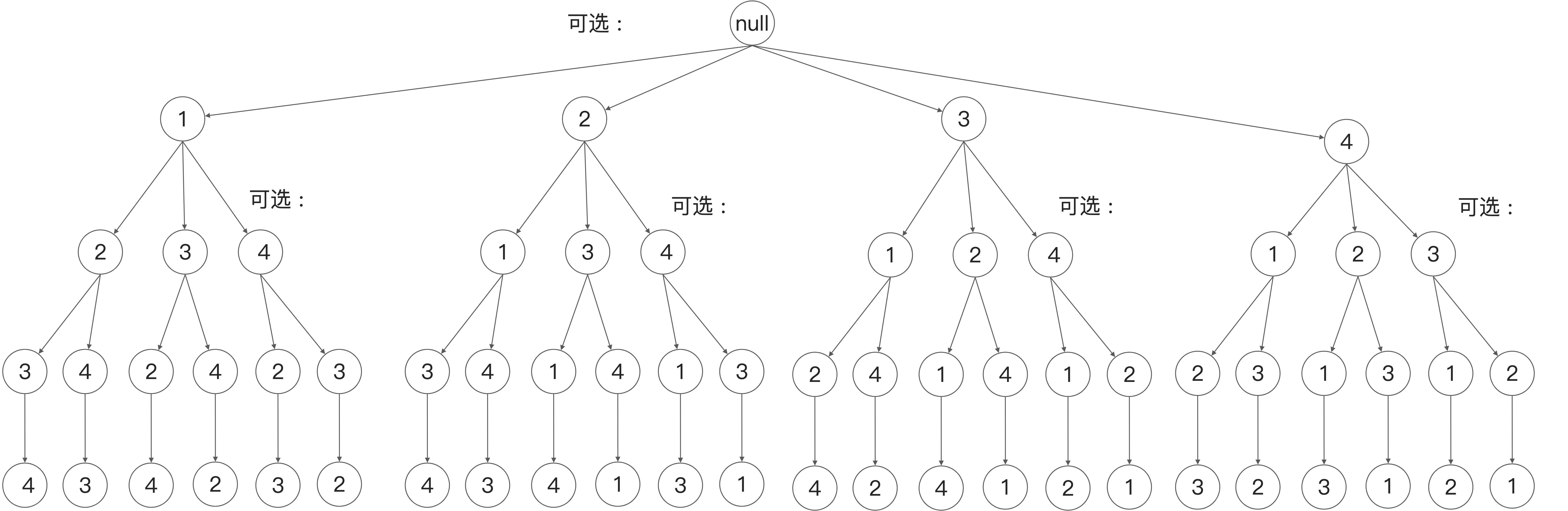
通过上图可知需要控制其可选列表即可,递归时可以通过传递**下标或者检查当前路径是否已经包含**即可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| class Solution {
List<List<Integer>> ret = new ArrayList<>();
public List<List<Integer>> permute(int[] nums) {
backtrack(nums,new LinkedList<>());
return ret;
}
public void backtrack(int[] nums,LinkedList<Integer> path){
if(path.size()==nums.length){
ret.add(new ArrayList<>(path));
return;
}
for(int num:nums){
if(path.contains(num))continue;
path.add(num);
backtrack(nums,path);
path.removeLast();
}
}
}
|
组合(相同的顺序)时的过滤方法是,建立一个visited数据组,通过判断当前分支
// visited[i - 1] == true,说明同一树支nums[i - 1]使用过
// visited[i - 1] == false,说明同一树层nums[i - 1]使用过
// 如果同一树层nums[i - 1]使用过则直接跳过
参考 [全排列III]
相关题目
给定两个整数 n 和 k,返回 1 … n 中所有可能的 k 个数的组合。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
public class Solution {
public List<List<Integer>> combine(int n, int k) {
List<List<Integer>> res = new ArrayList<>();
if (k <= 0 || n < k) {
return res;
}
Deque<Integer> path = new ArrayDeque<>(k);
dfs(1, n, k, path, res);
return res;
}
private void dfs(int begin, int n, int k, Deque<Integer> path, List<List<Integer>> res) {
if (k == 0) {
res.add(new ArrayList<>(path));
return;
}
if (begin > n - k + 1) {
return;
}
dfs(begin + 1, n, k, path, res);
path.addLast(begin);
dfs(begin + 1, n, k - 1, path, res);
path.removeLast();
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| class Solution {
List<List<Integer>> ret = new ArrayList<>();
public List<List<Integer>> combine(int n, int k) {
backtrack(n,k,1,new LinkedList<>());
return ret;
}
public void backtrack(int n,int k,int start,LinkedList<Integer> path){
if(path.size()==k){
ret.add(new ArrayList<>(path));
return;
}
for(int i=start;i<=n;i++){
path.add(i);
backtrack(n,k,i+1,path);
path.removeLast();
}
}
}
|
给定一个 没有重复 数字的序列,返回其所有可能的全排列。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| class Solution{
List<List<Integer>> res = new LinkedList<>();
List<List<Integer>> permute(int[] nums){
LinkedList<Integer> integers = new LinkedList<>();
backtrack(nums,integers);
return res;
}
public void backtrack(int[] nums, LinkedList<Integer> track){
if (nums.length==track.size()) {
res.add(new LinkedList(track));
return;
}
for (int i = 0; i <nums.length; i++) {
if (track.contains(nums[i]))continue;
track.add(nums[i]);
backtrack(nums,track);
track.removeLast();
}
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
| class Solution {
public List<List<Integer>> permuteUnique(int[] nums) {
List<List<Integer>> res = new ArrayList<>();
Arrays.sort(nums);
boolean[] visited = new boolean[nums.length];
backtrack(res, new ArrayList<>(), nums, visited, 0);
return res;
}
public void backtrack(List<List<Integer>> res, List<Integer> list, int[] nums, boolean[] visited, int n) {
if(n == nums.length) {
res.add(new ArrayList<>(list));
return;
}
for(int i = 0; i < nums.length; i++) {
if(visited[i] == true) continue;
if(i > 0 && nums[i] == nums[i - 1] && visited[i - 1] == false) continue;
visited[i] = true;
list.add(nums[i]);
backtrack(res, list, nums, visited, n + 1);
list.remove(list.size() - 1);
visited[i] = false;
}
}
}
|
递归和迭代拆分进行计算
1
2
3
4
5
6
7
8
9
10
11
| class Solution {
public double quickMul(double x, long N) {
if (N == 0) return 1.0;
double y = quickMul(x, N / 2);
return N % 2 == 0 ? y * y : y * y * x;
}
public double myPow(double x, int n) {
long N = n;
return N >= 0 ? quickMul(x, N) : 1.0 / quickMul(x, -N);
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| class Solution {
double quickMul(double x, long N) {
double ans = 1.0;
double x_contribute = x;
while (N > 0) {
if (N % 2 == 1) {
ans *= x_contribute;
}
x_contribute *= x_contribute;
N /= 2;
}
return ans;
}
public double myPow(double x, int n) {
long N = n;
return N >= 0 ? quickMul(x, N) : 1.0 / quickMul(x, -N);
}
}
|
给定一个大小为 n 的数组,找到其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素
哈希表,排序,摩尔投票
Boyer-Moore 投票算法
思路
如果我们把众数记为 +1,把其他数记为 −1,将它们全部加起来,显然和大于 0,从结果本身我们可以看出众数比其他数多。
算法
Boyer-Moore 算法的本质和方法四中的分治十分类似。我们首先给出 Boyer-Moore 算法的详细步骤:
1
2
3
4
5
| 我们维护一个候选众数 candidate 和它出现的次数 count。初始时 candidate 可以为任意值,count 为 0;
我们遍历数组 nums 中的所有元素,对于每个元素 x,在判断 x 之前,如果 count 的值为 0,我们先将 x 的值赋予 candidate,随后我们判断 x:
如果 x 与 candidate 相等,那么计数器 count 的值增加 1;
如果 x 与 candidate 不等,那么计数器 count 的值减少 1。
在遍历完成后,candidate 即为整个数组的众数。
|
我们举一个具体的例子,例如下面的这个数组:
[7, 7, 5, 7, 5, 1 | 5, 7 | 5, 5, 7, 7 | 7, 7, 7, 7]
在遍历到数组中的第一个元素以及每个在 | 之后的元素时,candidate 都会因为 count 的值变为 0 而发生改变。最后一次 candidate 的值从 5 变为 7,也就是这个数组中的众数。
Boyer-Moore 算法的正确性较难证明,这里给出一种较为详细的用例子辅助证明的思路,供读者参考:
首先我们根据算法步骤中对 count 的定义,可以发现:在对整个数组进行遍历的过程中,count 的值一定非负。这是因为如果 count 的值为 0,那么在这一轮遍历的开始时刻,我们会将 x 的值赋予 candidate 并在接下来的一步中将 count 的值增加 1。因此 count 的值在遍历的过程中一直保持非负。
那么 count 本身除了计数器之外,还有什么更深层次的意义呢?我们还是以数组
[7, 7, 5, 7, 5, 1 | 5, 7 | 5, 5, 7, 7 | 7, 7, 7, 7]
作为例子,首先写下它在每一步遍历时 candidate 和 count 的值:
nums: [7, 7, 5, 7, 5, 1 | 5, 7 | 5, 5, 7, 7 | 7, 7, 7, 7]
candidate: 7 7 7 7 7 7 5 5 5 5 5 5 7 7 7 7
count: 1 2 1 2 1 0 1 0 1 2 1 0 1 2 3 4
我们再定义一个变量 value,它和真正的众数 maj 绑定。在每一步遍历时,如果当前的数 x 和 maj 相等,那么 value 的值加 1,否则减 1。value 的实际意义即为:到当前的这一步遍历为止,众数出现的次数比非众数多出了多少次。我们将 value 的值也写在下方:
nums: [7, 7, 5, 7, 5, 1 | 5, 7 | 5, 5, 7, 7 | 7, 7, 7, 7]
value: 1 2 1 2 1 0 -1 0 -1 -2 -1 0 1 2 3 4
有没有发现什么?我们将 count 和 value 放在一起:
nums: [7, 7, 5, 7, 5, 1 | 5, 7 | 5, 5, 7, 7 | 7, 7, 7, 7]
count: 1 2 1 2 1 0 1 0 1 2 1 0 1 2 3 4
value: 1 2 1 2 1 0 -1 0 -1 -2 -1 0 1 2 3 4
发现在每一步遍历中,count 和 value 要么相等,要么互为相反数!并且在候选众数 candidate 就是 maj 时,它们相等,candidate 是其它的数时,它们互为相反数!
为什么会有这么奇妙的性质呢?这并不难证明:我们将候选众数 candidate 保持不变的连续的遍历称为「一段」。在同一段中,count 的值是根据 candidate == x 的判断进行加减的。那么如果 candidate 恰好为 maj,那么在这一段中,count 和 value 的变化是同步的;如果 candidate 不为 maj,那么在这一段中 count 和 value 的变化是相反的。因此就有了这样一个奇妙的性质。
这样以来,由于:
我们证明了 count 的值一直为非负,在最后一步遍历结束后也是如此;
由于 value 的值与真正的众数 maj 绑定,并且它表示「众数出现的次数比非众数多出了多少次」,那么在最后一步遍历结束后,value 的值为正数;
在最后一步遍历结束后,count 非负,value 为正数,所以它们不可能互为相反数,只可能相等,即 count == value。因此在最后「一段」中,count 的 value 的变化是同步的,也就是说,candidate 中存储的候选众数就是真正的众数 maj。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| class Solution {
public int majorityElement(int[] nums) {
int count = 0;
Integer candidate = null;
for (int num : nums) {
if (count == 0) {
candidate = num;
}
count += (num == candidate) ? 1 : -1;
}
return candidate;
}
}
|
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
| class Solution {
public List<String> letterCombinations(String digits) {
List<String> combinations = new ArrayList<String>();
if (digits.length() == 0) {
return combinations;
}
Map<Character, String> phoneMap = new HashMap<Character, String>() {{
put('2', "abc");
put('3', "def");
put('4', "ghi");
put('5', "jkl");
put('6', "mno");
put('7', "pqrs");
put('8', "tuv");
put('9', "wxyz");
}};
backtrack(combinations, phoneMap, digits, 0, new StringBuffer());
return combinations;
}
public void backtrack(List<String> combinations, Map<Character, String> phoneMap, String digits, int index, StringBuffer combination) {
if (index == digits.length()) {
combinations.add(combination.toString());
} else {
char digit = digits.charAt(index);
String letters = phoneMap.get(digit);
int lettersCount = letters.length();
for (int i = 0; i < lettersCount; i++) {
combination.append(letters.charAt(i));
backtrack(combinations, phoneMap, digits, index + 1, combination);
combination.deleteCharAt(index);
}
}
}
}
|
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。
后彼此不能相互攻击,也就是说:任何两个皇后都不能处于同一条横行、纵行或斜线上。
结题思路、回溯
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
| class Solution{
List<List<String>> res = new ArrayList<>();
public List<List<String>> solveNQueens(int n) {
char[][] board = new char[n][n];
for(int i = 0; i < n; i++){
Arrays.fill(board[i],'.');
}
backtrack(0,board);
return res;
}
public void backtrack(int row,char[][] board){
if(board.length == row){
res.add(charArraysToList(board));
return;
}
int n = board[row].length - 1;
for(int col = 0; col <= n; col++){
if (!isValid(board,row,col))
continue;
board[row][col]='Q';
backtrack(row+1,board);
board[row][col]='.';
}
}
public static boolean isValid(char[][] board,int row , int col){
int n = board.length;
for (int r = 0; r< n;r++){
if ( board[r][col] =='Q')
return false;
}
for (int i = row-1,j=col-1; i>=0&&j>=0;i--,j--){
if (board[i][j]=='Q')return false;
}
for (int i = row-1,j=col+1; i>=0&&j<board[i].length;i--,j++){
if (board[i][j]=='Q')return false;
}
return true;
}
public static List<String> charArraysToList(char[][] board){
List<String> list = new ArrayList<>();
for (char[] c : board){
String str = new String(c);
list.add(str);
}
return list;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
| class Solution {
int ret;
public int totalNQueens(int n) {
boolean[][] grid = new boolean[n][n];
backtrack(grid,0);
return ret;
}
public void backtrack(boolean[][] grid,int row){
int n = grid.length;
if(row==n){
ret++;
return;
}
for(int i=0;i<n;i++){
if(valid(grid,row,i)){
grid[row][i]=true;
backtrack(grid,row+1);
grid[row][i]=false;
}
}
}
public boolean valid(boolean[][] grid,int x,int y){
int n = grid.length;
for(int i=x,j=y;i>=0&&j>=0;i--,j--)if(grid[i][j])return false;
for(int i=x,j=y;i>=0&&j<n;i--,j++)if(grid[i][j])return false;
for(int i=0;i<=y;i++)if(grid[x][i])return false;
for(int i=0;i<=x;i++)if(grid[i][y])return false;
return true;
}
}
|
回溯思想、广度优先遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
| class Solution {
public int minMutation(String start, String end, String[] bank) {
HashSet<String> set = new HashSet<>(Arrays.asList(bank));
if (!set.contains(end)) {
return -1;
}
char[] four = {'A', 'C', 'G', 'T'};
Queue<String> queue = new LinkedList<>();
queue.offer(start);
set.remove(start);
int step = 0;
while (queue.size() > 0) {
step++;
for (int count = queue.size(); count > 0; --count) {
char[] temStringChars = queue.poll().toCharArray();
for (int i = 0, len = temStringChars.length; i < len; ++i) {
char oldChar = temStringChars[i];
for (int j = 0; j < 4; ++j) {
temStringChars[i] = four[j];
String newGenetic = new String(temStringChars);
if (end.equals(newGenetic)) {
return step;
} else if (set.contains(newGenetic)) {
set.remove(newGenetic);
queue.offer(newGenetic);
}
}
temStringChars[i] = oldChar;
}
}
}
return -1;
}
}
|
回溯思想、深度优先遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| class Solution {
int minStepCount = Integer.MAX_VALUE;
public int minMutation(String start, String end, String[] bank) {
dfs(new HashSet<String>(), 0, start, end, bank);
return (minStepCount == Integer.MAX_VALUE) ? -1 : minStepCount;
}
private void dfs (HashSet<String> step, int stepCount,String current, String end, String[] bank) {
if (current.equals(end)) minStepCount = Math.min(stepCount, minStepCount);
for (String str: bank) {
int diff = 0;
for (int i = 0; i < str.length(); i++)
if (current.charAt(i) != str.charAt(i)) if (++diff > 1) break;
if (diff == 1 && !step.contains(str)) {
step.add(str);
dfs(step, stepCount + 1, str, end, bank);
step.remove(str);
}
}
}
}
|
在每个树行中找最大值(中等)
广度优先
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| class Solution {
public List<Integer> largestValues(TreeNode root) {
List<Integer> ans = new ArrayList<Integer>();
LinkedList<TreeNode> queue = new LinkedList<>();
if(!Objects.isNull(root))queue.add(root);
while(!queue.isEmpty()){
int size = queue.size();
int max = queue.getFirst().val;
for(int i=0;i<size;i++){
TreeNode node = queue.poll();
if(node.val>max)max=node.val;
if(node.left!=null)queue.add(node.left);
if(node.right!=null)queue.add(node.right);
}
ans.add(max);
}
return ans;
}
}
|
306.累加数(mid)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
| class Solution {
boolean valid;
public boolean isAdditiveNumber(String num) {
if(num.length()==1)return false;
char[] nums = num.toCharArray();
int n = nums.length;
int num1 = 0;
for(int i=0,o=n;i<o;i++){
if(i==0&&nums[i]=='0')o=i+1;
num1=num1*10+nums[i]-'0';
int num2 = 0;
for(int j=i+1,l=n;j<l;j++){
if(j==i+1&&nums[j]=='0')l=j+1;
num2=num2*10+nums[j]-'0';
int num3 = 0;
for(int k=j+1,m=n;k<m;k++){
if(k==j+1&&nums[k]=='0')m=k+1;
num3=num3*10+nums[k]-'0';
if(num1+num2==num3)backtrack(nums,num2,num3,k+1);
if(valid) return valid;
}
}
}
return valid;
}
public void backtrack(char[] nums,int num1,int num2,int start){
int n = nums.length;
if(start==n){
valid = true;
return;
}
int num3 = 0;
for(int i=start,l=n;i<l;i++){
if(i==start&&nums[i]=='0')break;
num3=num3*10+nums[i]-'0';
if(num1+num2==num3){
backtrack(nums,num2,num3,i+1);
}
}
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| class Solution {
private List<String> ans = new ArrayList<>();
public List<String> restoreIpAddresses(String s) {
backtrace(s,0,new LinkedList<>());
return ans;
}
public void backtrace(String s,int index,LinkedList<String> path){
if(path.size()==4){
StringBuilder sb = new StringBuilder();
for(int i=0;i<4;i++){
sb.append(path.get(i));
if(i!=3)sb.append(".");
}
ans.add(sb.toString());
return;
}
for(int i=1;i<4&&index+i<=s.length();i++){
String addr = s.substring(index,index+i);
if(path.size()==3)addr = s.substring(index);
if(addr.length()>3||(addr.length()>1&&addr.charAt(0)=='0')||Integer.valueOf(addr)>255)continue;
path.add(addr);
backtrace(s,index+i,path);
path.removeLast();
if(path.size()==3)break;
}
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
| class Solution {
public List<String> generateParenthesis(int n) {
List<String> res = new ArrayList<String>();
generate(res, "", 0, 0, n);
return res;
}
public void generate(List<String> res , String ans, int count1, int count2, int n){
if(count1 > n || count2 > n) return;
if(count1 == n && count2 == n) res.add(ans);
if(count1 >= count2){
String ans1 = new String(ans);
generate(res, ans+"(", count1+1, count2, n);
generate(res, ans1+")", count1, count2+1, n);
}
}
List<String> ret = new ArrayList<>();
int size;
public List<String> generateParenthesis(int n) {
if(n==0)return ret;
size = 2 * n;
backtrack(new StringBuilder());
return ret;
}
public void backtrack(StringBuilder path){
if(path.length()==size){
if(valid(path))ret.add(path.toString());
return;
}
path.append('(');
backtrack(path);
path.deleteCharAt(path.length()-1);
path.append(')');
backtrack(path);
path.deleteCharAt(path.length()-1);
}
public boolean valid(StringBuilder sb){
int blance = 0;
for(int i=0;i<sb.length();i++){
char c = sb.charAt(i);
if(c=='(')++blance;
else --blance;
if(blance<0)return false;
}
return blance==0;
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| class Solution {
//思路:回溯
private List<List<Integer>> ans = new ArrayList<>();
private int[] candidates;
public List<List<Integer>> combinationSum(int[] candidates, int target) {
this.candidates = candidates;
backtrace(0,target,new LinkedList<Integer>());
return ans;
}
public void backtrace(int index,int target,LinkedList<Integer> path){
if (target<0)return;
if(0==target){
ans.add(new ArrayList<>(path));
return;
}
for (int i=index;i<candidates.length;i++){
path.add(candidates[i]);
target-=candidates[i];
backtrace(i,target,path);
path.removeLast();
target+=candidates[i];
}
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| class Solution {
List<List<Integer>> list=new ArrayList<>();
List<Integer> path=new ArrayList<>();
public List<List<Integer>> combinationSum2(int[] candidates, int target) {
Arrays.sort(candidates);
dfs(candidates,target,0);
return list;
}
private void dfs(int[] candidates, int target,int index){
if(target==0){
list.add(new ArrayList<>(path));
return;
}
for(int i=index;i<candidates.length;i++){
if(candidates[i]<=target){
//去重复
if(i>index&&candidates[i]==candidates[i-1])continue;
path.add(candidates[i]);
dfs(candidates,target-candidates[i],i+1);
path.remove(path.size()-1);
}
}
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| class Solution {
int[][] dirs = {{-1,0},{1,0},{0,-1},{0,1}};
int m,n;
public boolean exist(char[][] board, String word) {
m = board.length;
n = board[0].length;
for(int i=0;i<m;i++){
for(int j=0;j<n;j++){
if(board[i][j]==word.charAt(0)){
if(dfs(board,word,0,i,j))return true;
}
}
}
return false;
}
public boolean dfs(char[][] board,String word,int index,int x,int y){
if(index==word.length()-1)return true;
char c =board[x][y];board[x][y]='-';
for(int[] dir:dirs){
int newX = dir[0]+x,newY = dir[1]+y;
if(newX<m&&newX>=0&&newY<n&&newY>=0&&word.charAt(index+1)==board[newX][newY]){
if(dfs(board,word,index+1,newX,newY))return true;
}
}
board[x][y]=c;
return false;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| class Solution {
//思路:dfs
private int[][] dirs = {{-1,0},{1,0},{0,-1},{0,1}};
private int max,cloums,rows;
public int getMaximumGold(int[][] grid) {
rows = grid.length;
cloums = grid[0].length;
for(int i=0;i<rows;i++){
for(int j=0;j<cloums;j++){
if(grid[i][j]>0)dfs(grid,i,j,0);
}
}
return max;
}
public void dfs(int[][] grid,int x,int y,int count){
int gridv = grid[x][y];
count += gridv;
max=Math.max(max,count);
grid[x][y] = 0;
for(int[] dir:dirs){
int newX = dir[0]+x,newY = dir[1]+y;
if(newX>=0&&newX<rows&&newY>=0&&newY<cloums&&grid[newX][newY]>0){
dfs(grid,newX,newY,count);
}
}
grid[x][y] = gridv;
}
}
|
37.解数独(hard)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
| class Solution {
private boolean[][] line = new boolean[9][9];
private boolean[][] column = new boolean[9][9];
private boolean[][][] block = new boolean[3][3][9];
private boolean valid = false;
private List<int[]> spaces = new ArrayList<int[]>();
public void solveSudoku(char[][] board) {
for (int i = 0; i < 9; ++i) {
for (int j = 0; j < 9; ++j) {
if (board[i][j] == '.') {
spaces.add(new int[]{i, j});
} else {
int digit = board[i][j] - '0' - 1;
line[i][digit] = column[j][digit] = block[i / 3][j / 3][digit] = true;
}
}
}
dfs(board, 0);
}
public void dfs(char[][] board, int pos) {
if (pos == spaces.size()) {
valid = true;
return;
}
int[] space = spaces.get(pos);
int i = space[0], j = space[1];
for (int digit = 0; digit < 9 && !valid; ++digit) {
if (!line[i][digit] && !column[j][digit] && !block[i / 3][j / 3][digit]) {
line[i][digit] = column[j][digit] = block[i / 3][j / 3][digit] = true;
board[i][j] = (char) (digit + '0' + 1);
dfs(board, pos + 1);
line[i][digit] = column[j][digit] = block[i / 3][j / 3][digit] = false;
}
}
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| class Solution {
public List<TreeNode> generateTrees(int n) {
return n==0?new LinkedList<TreeNode>():generateTrees(1,n);
}
public List<TreeNode> generateTrees(int start,int end){
List<TreeNode> res = new LinkedList<TreeNode>();
if(start>end){
res.add(null);
return res;
}
for(int i=start;i<=end;i++){
List<TreeNode> subLeftTree = generateTrees(start,i-1);
List<TreeNode> subRightTree = generateTrees(i+1,end);
for(TreeNode left:subLeftTree){
for(TreeNode right:subRightTree){
TreeNode node = new TreeNode(i);
node.left = left;
node.right = right;
res.add(node);
}
}
}
return res;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| class Solution {
List<List<Integer>> ret = new ArrayList<>();
public List<List<Integer>> subsets(int[] nums) {
int n = nums.length;
if(n==0)return ret;
backtrack(nums,new LinkedList<Integer>(),0);
return ret;
}
public void backtrack(int[] nums,LinkedList<Integer> path,int index){
ret.add(new ArrayList<>(path));
for(int i=index;i<nums.length;i++){
path.add(nums[i]);
backtrack(nums,path,i+1);
path.removeLast();
}
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| class Solution {
List<List<Integer>> ret = new ArrayList<>();
public List<List<Integer>> subsetsWithDup(int[] nums) {
int n = nums.length;
boolean[] visited = new boolean[n];
Arrays.sort(nums);
backtrack(nums,visited,new LinkedList<>(),0);
return ret;
}
public void backtrack(int[] nums,boolean[] visited,LinkedList<Integer> path,int index){
ret.add(new ArrayList<>(path));
for(int i=index;i<nums.length;i++){
if(visited[i]||(i>0&&nums[i]==nums[i-1]&&!visited[i-1]))continue;
visited[i]=true;
path.add(nums[i]);
backtrack(nums,visited,path,i+1);
path.removeLast();
visited[i]=false;
}
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| class Solution {
List<String> ret = new ArrayList<>();
public String[] permutation(String s) {
char[] arr = s.toCharArray();
int n = arr.length;
Arrays.sort(arr);
boolean[] visited = new boolean[n];
backtrack(arr,visited,new StringBuilder());
return ret.toArray(new String[ret.size()]);
}
public void backtrack(char[] arr,boolean[] visited,StringBuilder sb){
if(sb.length()==arr.length){
ret.add(sb.toString());
return;
}
for(int i=0;i<arr.length;i++){
if(visited[i]||(i>0&&arr[i]==arr[i-1]&&!visited[i-1]))continue;
visited[i]=true;
sb.append(arr[i]);
backtrack(arr,visited,sb);
sb.deleteCharAt(sb.length()-1);
visited[i]=false;
}
}
}
|
1
2
3
4
5
6
7
8
9
10
|
class Solution {
public List<Integer> grayCode(int n) {
List<Integer> ret = new ArrayList<Integer>();
for (int i = 0; i < 1 << n; i++) {
ret.add((i >> 1) ^ i);
}
return ret;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| class Solution {
List<List<String>> ret = new ArrayList<>();
public List<List<String>> partition(String s) {
StringBuilder sb = new StringBuilder(s);
backtrack(sb,new LinkedList<String>(),0);
return ret;
}
public void backtrack(StringBuilder sb,LinkedList<String> path,int start){
if(start==sb.length())ret.add(new ArrayList<>(path));
for(int i=start+1;i<=sb.length();i++){
if(valid(sb,start,i-1)){
path.add(sb.substring(start,i));
backtrack(sb,path,i);
path.removeLast();
}
}
}
public boolean valid(StringBuilder sb,int left,int right){
while(left<right){
if(sb.charAt(left)!=sb.charAt(right))return false;
left++;right--;
}
return true;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
| class Solution {
public List<Integer> splitIntoFibonacci(String num) {
List<Integer> list = new ArrayList<Integer>();
backtrack(list, num, num.length(), 0, 0, 0);
return list;
}
public boolean backtrack(List<Integer> list, String num, int length, int index, int sum, int prev) {
if (index == length) return list.size() >= 3;
long currLong = 0;
for (int i = index; i < length; i++) {
if (i > index && num.charAt(index) == '0') {
break;
}
currLong = currLong * 10 + num.charAt(i) - '0';
if (currLong > Integer.MAX_VALUE) {
break;
}
int curr = (int) currLong;
if (list.size() >= 2) {
if (curr < sum) {
continue;
} else if (curr > sum) {
break;
}
}
list.add(curr);
if (backtrack(list, num, length, i + 1, prev + curr, curr)) {
return true;
} else {
list.remove(list.size() - 1);
}
}
return false;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| class Solution {
int max;
int ret;
public int countMaxOrSubsets(int[] nums) {
int n = nums.length;
for(int i=0;i<n;i++)max|=nums[i];
dfs(nums,0,0);
return ret;
}
public void dfs(int[] nums,int result,int p){
if(p==nums.length){
if(result==max)ret++;
return;
}
dfs(nums,result,p+1);
dfs(nums,result|nums[p],p+1);
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| class Solution {
List<String> ret = new ArrayList<>();
List<String> wordDict;
public List<String> wordBreak(String s, List<String> wordDict) {
this.wordDict = wordDict;
int n = s.length();
backtrack(s,new StringBuilder(),0);
return ret;
}
public void backtrack(String s,StringBuilder sb,int start){
if(start==s.length()){
sb.deleteCharAt(sb.length()-1);
ret.add(sb.toString());
return;
}
for(int i=start+1;i<=s.length();i++){
String str = s.substring(start,i);
if(wordDict.contains(str)){
int index = sb.length();
sb.append(str).append(' ');
backtrack(s,sb,i);
sb.delete(index,sb.length());
}
}
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
| public class Solution {
private boolean[] used;
private int[] factorial;
private int n;
private int k;
public String getPermutation(int n, int k) {
this.n = n;
this.k = k;
calculateFactorial(n);
used = new boolean[n + 1];
StringBuilder path = new StringBuilder();
dfs(0, path);
return path.toString();
}
private void dfs(int index, StringBuilder path) {
if (index == n) return;
int cnt = factorial[n - 1 - index];
for (int i = 1; i <= n; i++) {
if (used[i]) continue;
if (cnt < k) {
k -= cnt;
continue;
}
path.append(i);
used[i] = true;
dfs(index + 1, path);
return;
}
}
private void calculateFactorial(int n) {
factorial = new int[n + 1];
factorial[0] = 1;
for (int i = 1; i <= n; i++) {
factorial[i] = factorial[i - 1] * i;
}
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
| class Solution {
int min = Integer.MAX_VALUE;
int ret = Integer.MAX_VALUE;
int[] cookies;
public int distributeCookies(int[] cookies, int k) {
this.cookies = cookies;
distributeCookies(0,new int[k]);
return ret;
}
private void distributeCookies(int index,int[] sum) {
if (index==cookies.length){
int max = Arrays.stream(sum).max().getAsInt();
int min = Arrays.stream(sum).min().getAsInt();
if (max == 0 || min == 0 )return;
if (max-min<this.min){
ret = max;
this.min = max - min;
}
return;
}
for (int i = 0; i < sum.length; i++) {
sum[i]+=cookies[index];
if(sum[i]<ret){
distributeCookies(index+1,sum);
}
sum[i]-=cookies[index];
}
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
| class Solution {
public int minimumTimeRequired(int[] jobs, int k) {
Arrays.sort(jobs);
int low = 0, high = jobs.length - 1;
while (low < high) {
int temp = jobs[low];
jobs[low] = jobs[high];
jobs[high] = temp;
low++;
high--;
}
int l = jobs[0], r = Arrays.stream(jobs).sum();
while (l < r) {
int mid = (l + r) >> 1;
if (check(jobs, k, mid)) {
r = mid;
} else {
l = mid + 1;
}
}
return l;
}
public boolean check(int[] jobs, int k, int limit) {
int[] workloads = new int[k];
return backtrack(jobs, workloads, 0, limit);
}
public boolean backtrack(int[] jobs, int[] workloads, int i, int limit) {
if (i >= jobs.length) {
return true;
}
int cur = jobs[i];
for (int j = 0; j < workloads.length; ++j) {
if (workloads[j] + cur <= limit) {
workloads[j] += cur;
if (backtrack(jobs, workloads, i + 1, limit)) {
return true;
}
workloads[j] -= cur;
}
if (workloads[j] == 0 || workloads[j] + cur == limit) {
break;
}
}
return false;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
| public boolean makesquare(int[] matchsticks) {
int totalLen = Arrays.stream(matchsticks).sum();
if (totalLen % 4 != 0) {
return false;
}
Arrays.sort(matchsticks);//排序
//降序
for (int i = 0, j = matchsticks.length - 1; i < j; i++, j--) {
int temp = matchsticks[i];
matchsticks[i] = matchsticks[j];
matchsticks[j] = temp;
}
//四条边
int[] edges = new int[4];
//进行dfs
return dfs(0, matchsticks, edges, totalLen / 4);
}
//dfs回溯
public boolean dfs(int index, int[] matchsticks, int[] edges, int len) {
//如果下标==matchsticks.length说明数组已经遍历完成,此时返回true
if (index == matchsticks.length) {
return true;
}
//遍历四条边,判断当前火柴可以加在那个边上,再进行dfs
for (int i = 0; i < edges.length; i++) {
//加在当前边上
edges[i] += matchsticks[index];
//如果小于等于len且在进行下一轮dfs
if (edges[i] <= len && dfs(index + 1, matchsticks, edges, len)) {
//如果dfs返回true则直接返回ture无需再遍历了
return true;
}
//从当前边上移除(取消选择)
edges[i] -= matchsticks[index];
}
return false;
}
|
相关资料


