算法笔记-排序算法

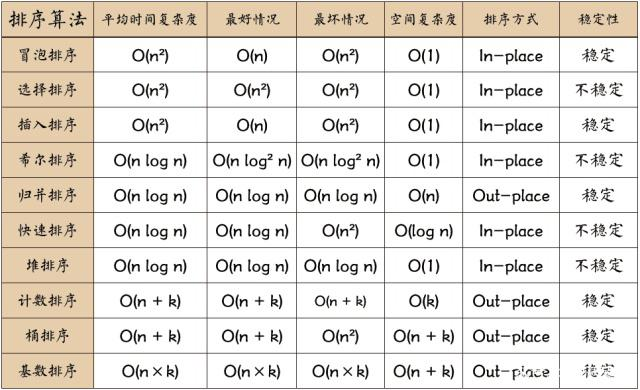
排序算法

算法篇-排序算法

nlogn排序: 堆排序、快速排序、归并排序

初级排序

O(n^2)

  • 选择排序(Select Sort)每次找最小值，然后放到待排序数组的起始位置。
  • 插入排序(Insert Sort)从前到后逐步构建有序序列；对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。
  • 冒泡排序(Bubble Sort)嵌套循环，每次查看相邻的元素如果逆序，则交换。

高级排序

O(n*logn)

  • 快速排序(Quick Sort)数组取标杆pivot，将小元素放pivot左边，大元素放右边，然后依次对右边和左边的子数组继续快排；以达到整个序列有序
  • 归并排序(Merge Sort)

1.把长度为n的输入序列分成两个长度位n/2的子序列;
2.把这两个子序列分别采用归并排序;
3.将两个排序好的子序列合并成一个最终的排序序列;

归并排序和快速排序具有相似性，但步骤相反

归并:先排序左右子数组，然后合并两个有序子数组

快排:先调出左右子数组，然后对于左右数组进行排序

  • 对排序(heap Sort)　堆插入O(logN)，取最大最小值O(1)

1.数组元素依次建立小堆顶
2.依次取堆顶元素，并删除

(满二叉搜索树进行实现)

拓扑排序

对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序，是将G中所有顶点排成一个线性序列，使得图中任意一对顶点u和v，若边<u,v>∈E(G)，则u在线性序列中出现在v之前。通常，这样的线性序列称为满足拓扑次序(Topological Order)的序列，简称拓扑序列。简单的说，由某个集合上的一个偏序得到该集合上的一个全序，这个操作称之为拓扑排序。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
queue<int>q;
//priority_queue<int,vector<int>,greater<int>>q;
//优先队列的话，会按照数值大小有顺序的输出
//此处为了理解，暂时就用简单队列
int topo(){
    for(inti=1;i<=n;i++)
    {
        if(indegree[i]==0)
        {
            q.push(i);
        }
    }
 
    int temp;
    while(!q.empty())
    {
        temp=q.front();//如果是优先队列，这里可以是top()
        printf("%d->",temp);
        q.pop();
        for(inti=1;i<=n;i++)//遍历从temp出发的每一条边，入度--
        {
            if(map[temp][i])
            {
                indegree[i]--;
                if(indegree[i]==0)q.push(i);
            }
        }
    }
}

先复习一波

相关题目

TopK问题(中等)

top-k问题 主要解法：排序、堆、随机快速选择、BFPRT 排序方法：时间复杂度O(NlogN)， 因为本题数据特殊性 可以使用计数排序 时间复杂度O(N)
堆：维护一个大小为k的堆， 不太建议使用priority_queue, 额外空间和数据拷贝，可以原地操作数组，使用make_heap + pop_heap、push_heap 或 覆盖堆顶，自实现堆顶下沉 时间复杂度O(Nlogk)
随机快速选择：平均时间复杂度 O(N)
BFPRT：最坏时间复杂度 O(N)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    /**
     * 小顶堆（min-heap）有个重要的性质——每个结点的值均不大于其左右孩子结点的值，则堆顶元素即为整个堆的最小值。JDK中PriorityQueue实现了数据结构堆，通过指定comparator字段来表示小顶堆或大顶堆，默认为null，表示自然序（natural ordering）。
     * 小顶堆解决Top K问题的思路：小顶堆维护当前扫描到的最大100个数，其后每一次的扫描到的元素，若大于堆顶，则入堆，然后删除堆顶；依此往复，直至扫描完所有元素。Java实现第K大整数代码如下：
     * @param nums
     * @param k
     * @return
     */
    public int findKthLargest(int[] nums, int k) {
        PriorityQueue<Integer> minQueue = new PriorityQueue<>(k);
        for (int num : nums) {
            if (minQueue.size() < k || num > minQueue.peek())
                minQueue.offer(num);
            if (minQueue.size() > k)
                minQueue.poll();
        }
        return minQueue.peek();
    }
}

快排解题思路

我们知道，经过快速排序算法中的一次划分后，基点左边的所有数小于基点，右边的所有数大于基点，基点位置pivot有三种情况：

  • pivot == k 说明基点就是第k+1个小的元素，其左边的子数组就是最小的k个数。此时的子数组[0, k) 就是答案
  • pivot > k 说明基点”偏大”了，对其左子数组继续进行划分
  • pivot < k 说明基点”偏小”了，对其右子数组继续进行划分

快排代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
/**
 * 快速排序
 */
class Solution {
    Random random = new Random();
    //函数入口
    public int findKthLargest(int[] nums, int k) {
        // 要找到的元素所在索引:  前K大，即倒数索引第K个
        int index = nums.length - k;
        int right = nums.length - 1;
        int left = 0;
        return quickSelect(nums, left, right, index);
    }
    //快排选择
    public int quickSelect(int[] nums, int left, int right, int index) {
        // 得到分区值索引q
        int q = randomPartition(nums, left, right);

        if (q == index) {
            // 如果刚好索引q就是想要的索引，则直接返回
            return nums[q];

        } else {
            // 如果不是，比较q 与 index ,确定下次要检索的区间, 要么是[q+1, right], 要么就是[left, q-1]
            return q < index ? quickSelect(nums, q + 1, right, index) : quickSelect(nums, left, q - 1, index);
        }
    }
    //随机分区
    public int randomPartition(int[] nums, int l, int r) {
        // 1. 随机数范围: [0, r-l+1) 同时加l, 则是 [l, r+1) = [l, r] 也就是在这个[l,r] 中随机选一个索引出来
        int i = random.nextInt(r - l + 1) + l;
        // 2. 交换nums[i]， nums[r], 也就是将随机数先放在[l,r]最右边nums[r]上
        swap(nums, i, r);
        return partition(nums, l, r);
    }
    //
    public int partition(int[] nums, int l, int r) {
        // 3. 在调用当前方法的randomPartition方法中，已经确定了了随机数是nums[r]
        int x = nums[r], i = l - 1;

        // 首先比较区间在[l， r]之间， 所以nums[j]中的    l<= j <= r
        for (int j = l; j < r; ++j) {
            // 4. nums[j] 跟随机数 x 比较, 小于x的数都跟[l,r]左边区间交换，i=l-1,所以++i=l,初始索引就是l,
            if (nums[j] <= x) {
                swap(nums, ++i, j);//两两交换
            }
        }// 这个for循环操作就是将小于 x 的数都往[i, j]的左边区间设置，从而实现存在[l, i]区间,使得对应数值都 小于 x

        //5. 既然已经将<x的值都放在一边了，现在将x也就是nums[r] 跟nums[i+1]交换，从而分成两个区间[l.i+1]左, [i+2, r]右，左边区间的值都小于x
        swap(nums, i + 1, r);

        // 然后返回这个分区值
        return i + 1;
    }
    //交换位置
    public void swap(int[] a, int i, int j) {
        int temp = a[i];
        a[i] = a[j];
        a[j] = temp;
    }
}

BFPRT算法思路(O(n))

BFPRT算法又称中位数的中位数算法，可以用于在O(n)的时间复杂度内找到第k小的数。对于本题，我们可以用BFPRT算法找到第k小的数O(n)，然后遍历一遍原数组O(n)，将小于第k小的数的元素加入到答案数组，即得正确解(时间复杂度也是O(n))。

BFPRT算法的主要步骤如下：

  • 将 [公式] 个元素划为 [公式] 组，每组5个，至多只有一组由 [公式] 个元素组成。
  • 寻找这 [公式] 个组中每一个组的中位数，这个过程可以用插入排序。
  • 对步骤2中的 [公式] 个中位数，重复步骤1和步骤2，递归下去，直到剩下一个数字。
  • 最终剩下的数字即为pivot，把大于它的数全放左边，小于等于它的数全放右边。
  • 判断pivot的位置与k的大小，有选择的对左边或右边递归。

中位数的中位数算法

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
#include <iostream>
#include <algorithm>

using namespace std;

int InsertSort(int array[], int left, int right);
int GetPivotIndex(int array[], int left, int right);
int Partition(int array[], int left, int right, int pivot_index);
int BFPRT(int array[], int left, int right, int k);

int main()
{
    int k = 8; // 1 <= k <= array.size
    int array[20] = { 11,9,10,1,13,8,15,0,16,2,17,5,14,3,6,18,12,7,19,4 };

    cout << "原数组：";
    for (int i = 0; i < 20; i++)
        cout << array[i] << " ";
    cout << endl;

    // 因为是以 k 为划分，所以还可以求出第 k 小值
    cout << "第 " << k << " 小值为：" << array[BFPRT(array, 0, 19, k)] << endl;

    cout << "变换后的数组：";
    for (int i = 0; i < 20; i++)
        cout << array[i] << " ";
    cout << endl;

    return 0;
}

/**
 * 对数组 array[left, right] 进行插入排序，并返回 [left, right]
 * 的中位数。
 */
int InsertSort(int array[], int left, int right)
{
    int temp;
    int j;

    for (int i = left + 1; i <= right; i++)
    {
        temp = array[i];
        j = i - 1;

        while (j >= left && array[j] > temp)
        {
            array[j + 1] = array[j];
            j--;
        }

        array[j + 1] = temp;
    }

    return ((right - left) >> 1) + left;
}

/**
 * 数组 array[left, right] 每五个元素作为一组，并计算每组的中位数，
 * 最后返回这些中位数的中位数下标（即主元下标）。
 *
 * @attention 末尾返回语句最后一个参数多加一个 1 的作用其实就是向上取整的意思，
 * 这样可以始终保持 k 大于 0。
 */
int GetPivotIndex(int array[], int left, int right)
{
    if (right - left < 5)
        return InsertSort(array, left, right);

    int sub_right = left - 1;

    // 每五个作为一组，求出中位数，并把这些中位数全部依次移动到数组左边
    for (int i = left; i + 4 <= right; i += 5)
    {
        int index = InsertSort(array, i, i + 4);
        swap(array[++sub_right], array[index]);
    }

    // 利用 BFPRT 得到这些中位数的中位数下标（即主元下标）
    return BFPRT(array, left, sub_right, ((sub_right - left + 1) >> 1) + 1);
}

/**
 * 利用主元下标 pivot_index 进行对数组 array[left, right] 划分，并返回
 * 划分后的分界线下标。
 */
int Partition(int array[], int left, int right, int pivot_index)
{
    swap(array[pivot_index], array[right]); // 把主元放置于末尾

    int partition_index = left; // 跟踪划分的分界线
    for (int i = left; i < right; i++)
    {
        if (array[i] < array[right])
        {
            swap(array[partition_index++], array[i]); // 比主元小的都放在左侧
        }
    }

    swap(array[partition_index], array[right]); // 最后把主元换回来

    return partition_index;
}

/**
 * 返回数组 array[left, right] 的第 k 小数的下标
 */
int BFPRT(int array[], int left, int right, int k)
{
    int pivot_index = GetPivotIndex(array, left, right); // 得到中位数的中位数下标（即主元下标）
    int partition_index = Partition(array, left, right, pivot_index); // 进行划分，返回划分边界
    int num = partition_index - left + 1;

    if (num == k)
        return partition_index;
    else if (num > k)
        return BFPRT(array, left, partition_index - 1, k);
    else
        return BFPRT(array, partition_index + 1, right, k - num);
}

Top K问题的两种解决思路

最小的k个数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
class Solution {
    //堆
    public int[] getLeastNumbers(int[] arr, int k){
        return getLeastNumbersByQuickSort(arr,k);
        //return getLeastNumbersByHeap(arr,k);
        //return getLeastNumbersBySort(ans,k);
    }
    //快排变体:不对整个数组进行排序，定位到第k小的数即0-k的数就是答案
    public int[] getLeastNumbersByQuickSort(int[] arr, int k) {
        int[] ans = new int[k];
        quickSort(arr, 0, arr.length - 1, k-1);
        for(int i=0;i<k;i++)ans[i]=arr[i];
        return ans;
    }
    public void quickSort(int[] arr,int left,int right,int k){
        if(left<right){
            int low = left,height = right,base = arr[left];
            while(low<height){
                while(low<height&&arr[height]>=base)height--;
                if(low<height)arr[low++] = arr[height];
                while(low<height&&arr[low]<base)low++;
                if(low<height)arr[height--] = arr[low];
            }
            arr[low] = base;
            if(low==k)return;
            if(low>k)quickSort(arr,left,low-1,k);//说明在k左区间
            else quickSort(arr,low+1,right,k);//k在右边区间
        }
    }

    //堆
    public int[] getLeastNumbersByHeap(int[] arr, int k) {
        if (k == 0 || arr.length == 0) return new int[0];
        int[] ans = new int[k];
        PriorityQueue<Integer> minQueue = new PriorityQueue<>((v1,v2)->v2-v1);
        for(int num:arr){
            if(minQueue.size()<k)minQueue.offer(num);
            else if(minQueue.peek()>num){
                minQueue.poll();
                minQueue.offer(num);
            }
        }
        int i=0;
        for(int n:minQueue)ans[i++]=n;
        return ans;
    }
    //直接排序
    public int[] getLeastNumbersBySort(int[] arr, int k) {
        int[] ans = new int[k];
        quickSort(arr,0,arr.length-1);
        for(int i=0;i<k;i++)ans[i]=arr[i];
        return ans;
    }
    public void quickSort(int[] arr,int left,int right){
        if(left<right){
            int low = left,height = right,base = arr[left];
            while(low<height){
                while(low<height&&arr[height]>=base)height--;
                if(low<height)arr[low++] = arr[height];
                while(low<height&&arr[low]<base)low++;
                if(low<height)arr[height--] = arr[low];
            }
            arr[low] = base;
            quickSort(arr,left,low-1);
            quickSort(arr,low+1,right);
        }
    }
}

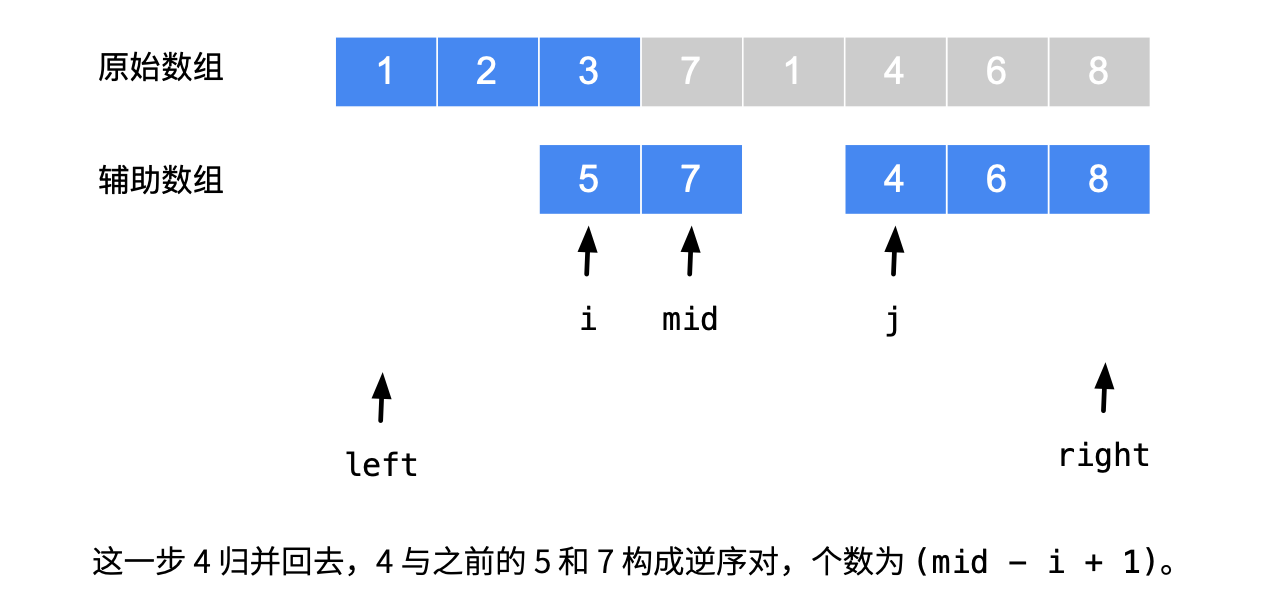
剑指 Offer 51. 数组中的逆序对（hard）

在归并的过程中将原始数组一分为二，分别对其进行排序，排序完成后进行合并，每次将两个有序数组中的较小的数放入新数组中，在这合并的过程中每当我们选取右边数组的数加入新数组时，能与它组成的逆序数就是左边数组剩余的个数（因为在原始数组中右边数组每个数都在左边数组的右边且当前左边剩余的数都比当前要插入新数组的数大），当选取的是左边的数时无需再重复计数（已经递归计算过）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
class Solution {
    //先来一段归并排序的代码
    void merge(int[] arr, int start, int end) {
        if (start == end) return;
        int mid = (start + end) / 2;
        merge(arr, start, mid);
        merge(arr, mid + 1, end);

        int[] temp = new int[end - start + 1];
        int i = start, j = mid + 1, k = 0;
        while (i <= mid && j <= end)
            temp[k++] = arr[i] < arr[j] ? arr[i++] : arr[j++];
        while (i <= mid)
            temp[k++] = arr[i++];
        while (j <= end)
            temp[k++] = arr[j++];
        System.arraycopy(temp, 0, arr, start, end);
    }

    //再看一下这道题的题解
    public int reversePairs(int[] nums) {
        return mergeSort(nums,0,nums.length-1);
    }
    public int mergeSort(int[] nums,int left,int right){
        if(left==right||right<left)return 0;
        int mid = left+(right-left)/2;
        //排序两个数组
        int ret = mergeSort(nums,left,mid)+mergeSort(nums,mid+1,right);
        //合并两个数组
        int index = 0;
        int i = left,j = mid+1;
        int[] temp = new int[right-left+1];
        while(i<=mid&&j<=right){
            //如果当前元素是右边排序数组的则计算其左边排序数组的未排序个数
            ret+=nums[i]>nums[j]?mid-i+1:0;
            temp[index++] = nums[i]>nums[j]?nums[j++]:nums[i++];
        }
        //左边数组没排完继续排
        while(i<=mid){
            temp[index++] = nums[i++];
        }
        //右边数组没排完继续排
        while(j<=right){
            temp[index++] = nums[j++];
        }
        //复制到原始数组中的位置
        for(int k=left,l=0;k<=right;k++,l++){
            nums[k] = temp[l];
        }
        return ret;
    }
}

子集(中等)

给你一个整数数组 nums ，返回该数组所有可能的子集（幂集）。解集不能包含重复的子集。

1
2
3
4
5
6
7
示例 1：
输入：nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

示例 2：
输入：nums = [0]
输出：[[],[0]]

字典排序(二进制排序)

nums=[5,2,9]

0/1 序列 子集 0/1 0/1 序列对应的二进制数
000 {} 0
001 {9} 1
010 {2} 2
011 {2,9} 3
100 {5} 4
101 {5,9} 5
110 {5,2} 6
111 {5,2,9} 7 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    List<Integer> t = new ArrayList<Integer>();
    List<List<Integer>> ans = new ArrayList<List<Integer>>();
    public List<List<Integer>> subsets(int[] nums) {
        int n = nums.length;
        for (int mask = 0; mask < (1 << n); ++mask) {//左移乘2
            t.clear();
            for (int i = 0; i < n; ++i) {
                //i为数组长度
                //mask为二进制对应的数 0-2^n
                //1<<i左移位数　并且按位与(&) 当为1时证明当前数=mask
                if ((mask & (1 << i)) != 0) {//判断是否已经存在子集当中
                    t.add(nums[i]);
                }
            }
            ans.add(new ArrayList<Integer>(t));
        }
        return ans;
    }
}

递归回溯，深度优先遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    //存储
    List<Integer> t = new ArrayList<Integer>();
    List<List<Integer>> ans = new ArrayList<List<Integer>>();
    //方法入口
    public List<List<Integer>> subsets(int[] nums) {
        dfs(0, nums);
        return ans;
    }
    //深度遍历
    public void dfs(int cur, int[] nums) {
        if (cur == nums.length) {//递归结束条件
            ans.add(new ArrayList<Integer>(t));
            return;
        }
        t.add(nums[cur]);//添加到当前记录结果
        dfs(cur + 1, nums);//递归调用
        t.remove(t.size() - 1);//移除当前末尾元素
        dfs(cur + 1, nums);//递归调用
    }
}

qi

前K个高频元素

本题和TopK有些类似，题目要优于NlogN，可以采用堆这种结构进行存储，设置堆大小为k，当堆存储个数小于k直接插入，否则比较新的元素和堆顶元素频率，留下频率高的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
    public int[] topKFrequent(int[] nums, int k) {
        Map<Integer, Integer> occurrences = new HashMap<Integer, Integer>();
        for (int num : nums) occurrences.put(num, occurrences.getOrDefault(num, 0) + 1);
        // int[] 的第一个元素代表数组的值，第二个元素代表了该值出现的次数
        PriorityQueue<int[]> queue = new PriorityQueue<int[]>(new Comparator<int[]>() {
            public int compare(int[] m, int[] n) {
                return m[1] - n[1];
            }
        });
        for (Map.Entry<Integer, Integer> entry : occurrences.entrySet()) {
            int num = entry.getKey(), count = entry.getValue();
            if (queue.size() == k) {
                if (queue.peek()[1] < count) {
                    queue.poll();
                    queue.offer(new int[]{num, count});
                }
            } else {
                queue.offer(new int[]{num, count});
            }
        }
        int[] ret = new int[k];
        for (int i = 0; i < k; ++i) {
            ret[i] = queue.poll()[0];
        }
        return ret;
    }
}

基于快排，通过map进行统计每个元素的出现次数，然后通过对元素出现的次数（次数次数次数重要的事情说三遍）进行排序即可取出前k个得出答案。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
//基于快排
//我们知道快速排序每次会划分为两个区间,arr[i…q−1] 与 arr[q+1…j],其左边区间的个数为q-i个,再判断是否为k
// 1.如果 k≤q−i，则数组 arr[l…r] 前 k 大的值，就等于子数组 arr[i…q−1] 前 k 大的值。
// 2.否则，数组 arr[l…r] 前 k 大的值，就等于左侧子数组全部元素，加上右侧子数组 arr[q+1…j] 中前 k−(q−i) 大的值。
class Solution {
    public int[] topKFrequent(int[] nums, int k) {
        Map<Integer,Integer> map = new HashMap<>();
        for(int n:nums)map.put(n,map.getOrDefault(n,0)+1);
        List<int[]> list = new ArrayList<>();
        for(int key:map.keySet())list.add(new int[]{key,map.get(key)});
        int[] ret = new int[k];
        qsort(list,0,list.size()-1,ret,0,k);
        return ret;
    }
    public void qsort(List<int[]> values, int start, int end, int[] ret, int retIndex, int k) {
        int picked = (int)(Math.random()*(end-start+1))+start;//随机基准
        Collections.swap(values,picked,start);//交换
        int pivot = values.get(start)[1];
        int index = start;
        for(int i=start+1;i<=end;i++){//从前面查找比基准大的数与其进行交换
            if(values.get(i)[1]>=pivot){
                Collections.swap(values,index+1,i);
                index++;
            }
        }
        Collections.swap(values,start,index);//交换
        //排序的个数小于k说明还需要向右区间排序
        if(k<=index-start){
            qsort(values,start,index-1,ret,retIndex,k);
        }else{
            //否则排序好则直接赋值
            for(int i=start;i<=index;i++){
                ret[retIndex++] = values.get(i)[0];
            }
            //如果左区间个数大于k则需要进一步排序
            if(k>index-start+1){
                qsort(values,index+1,end,ret,retIndex,k-(index-start+1));
            }
        }
    }
}

349. 两个数组的交集（easy）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
    public int[] intersection(int[] nums1, int[] nums2) {
        Arrays.sort(nums1);//[4,5,9]
        Arrays.sort(nums2);//[4,4,8,9,9]
        int m = nums1.length;
        int n = nums2.length;
        List<Integer> list = new ArrayList<>();
        int l1 = 0,l2 = 0;
        while (l1<m||l2<n){
            //same
            if (l1<m&&l2<n&&nums1[l1]==nums2[l2]){
                list.add(nums1[l1]);
                while (l1<m-1&&nums1[l1]==nums1[l1+1])l1++;
                while (l2<n-1&&nums2[l2]==nums2[l2+1])l2++;
                l1++;
                l2++;
            }else if((l1<m&&l2<n&&nums1[l1]<nums2[l2])||l2>=n){
                while (l1<m-1&&nums1[l1]==nums1[l1+1])l1++;
                l1++;
            } else {
                while (l2<n-1&&nums2[l2]==nums2[l2+1])l2++;
                l2++;
            }
        }
        //convert ret
        int[] ret = new int[list.size()];
        for(int i=0;i<list.size();i++){
            ret[i] = list.get(i);
        }
        return ret;
    }
}

350. 两个数组的交集 II（easy）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
    //哈希表、排序+双指针
    public int[] intersect(int[] nums1, int[] nums2) {
        int n1 = nums1.length;
        int n2 = nums2.length;
        Arrays.sort(nums1);
        Arrays.sort(nums2);
        List<Integer> list = new ArrayList<>();
        //4,5,9
        //4，4，8，9，9
        int i1 = 0;
        int i2 = 0;
        while(i1<n1&&i2<n2){
            if(nums1[i1]==nums2[i2]){
                list.add(nums1[i1]);
                i1++;
                i2++;
            }else if(nums1[i1]>nums2[i2]){
                i2++;
            }else if(nums1[i1]<nums2[i2]){
                i1++;
            }
        }
        int[] ret = new int[list.size()];
        for(int i=0;i<list.size();i++)ret[i]=list.get(i);
        return ret;
    }
}

252. 会议室（easy）

1
2
3
4
5
6
7
8
9
10
11
class Solution {
    public boolean canAttendMeetings(int[][] intervals) {
        int n = intervals.length;
        if(n==0)return true;
        Arrays.sort(intervals,(o1,o2)->o1[0]-o2[0]);
        for(int i=1;i<n;i++){
            if(intervals[i][0]<intervals[i-1][1])return false;
        }
        return true;
    }
}

253. 会议室 II（mid)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    //思路：计算重叠区间,如果存在n场会议重叠则需要n个会议室
    //抄别人的优先队列
    public int minMeetingRooms(int[][] intervals) {
        if(intervals==null||intervals.length==0) return 0;
        // 按结束时间排序(小堆顶)
    	PriorityQueue<Integer> queue = new PriorityQueue<Integer>();
        // 按开始时间排序
    	Arrays.sort(intervals,(i,j)->i[0]-j[0]);
    	queue.add(intervals[0][1]);
    	for(int i=1;i!=intervals.length;i++) {
    		int last=queue.peek();//最早结束的
    		if(last<=intervals[i][0]) { // 最早结束的可以腾出会议室
    			queue.poll();
    		    queue.add(intervals[i][1]); //修改该会议室的结束时间
            }else{ //最早结束的都来不及腾出会议室
                queue.add(intervals[i][1]);// 需要一个新的会议室
            }
    	}
    	return queue.size();
    }
}

242. 有效的字母异位词（easy）

1
2
3
4
5
6
7
8
9
10
class Solution {
    public boolean isAnagram(String s, String t) {
        if(s.length()!=t.length())return false;
        char[] sa = s.toCharArray();
        char[] ta = t.toCharArray();
        Arrays.sort(sa);
        Arrays.sort(ta);
        return Arrays.equals(sa,ta);
    }
}

剑指 Offer 45. 把数组排成最小的数（mid)

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
    //按照字典序排序 (x,y)->(x+y).compareTo(y+x)
    public String minNumber(int[] nums) {
        int n = nums.length;
        StringBuilder sb = new StringBuilder();
        String[] strs = new String[n];
        for(int i=0;i<n;i++)strs[i] = String.valueOf(nums[i]);
        Arrays.sort(strs,(x,y)->(x+y).compareTo(y+x));
        for(String str:strs)sb.append(str);
        return sb.toString();
    }
}

280. 摆动排序（mid）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
    //比较当前元素与下一个元素。若顺序不正确，则交换之。
    public void wiggleSort(int[] nums) {
      boolean less = true;
      for (int i = 0; i < nums.length - 1; i++) {
          if (less) {
            if (nums[i] > nums[i + 1]) {
                swap(nums, i, i + 1);
            }
          } else { 
              if (nums[i] < nums[i + 1]) {
                swap(nums, i, i + 1);
              }
          }
          less = !less;
        }
    }
    //精简版
    public void wiggleSort(int[] nums) {
        for (int i = 0; i < nums.length - 1; i++) {
            if ((i % 2 == 0) == (nums[i] > nums[i + 1])) {
                swap(nums, i, i + 1);
            }
        }
    }
    private void swap(int[] nums, int i, int j) {
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }
}

324. 摆动排序 II（mid)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    //奇数位下标值比两边大
    //思路：排序成升序，123456，如果直接分割成两半123，456进行插入得162534
    //但是如果输入是[12446],分割插入得到[16244],末尾两个元素相等了,但是存在[4,6,2,4,1]是成立的,所以通过两次插入来解决这个问题
    //第一次插入大数在奇数下标,从排序的末尾向前如6->4,得到x6x4x,
    //第二次插入小数在偶数下标,从排序的末尾向前如4->2->1,得到46241
    public void wiggleSort(int[] nums) {
        int[] help = nums.clone(); //不能写成int[] help = nums,排序后两个数组都改变
        Arrays.sort(help);
        int N = nums.length;
        //比如123456
        for (int i = 1; i < nums.length; i += 2) {
            nums[i] = help[--N]; //遍历完成后 x 6 x 5 x 4 
        }
        for (int i = 0; i < nums.length; i += 2) {
            nums[i] = help[--N]; //便利完成后 3 6 2 5 1 4
        }
    }
}

179. 最大数

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
    public String largestNumber(int[] nums) {
        int n = nums.length;
        String[] strs = new String[n];
        for(int i=0;i<n;i++)strs[i]=String.valueOf(nums[i]);
        //排序：1+2字典序=12,2+1的字典序21，大于12,按照升序排序(大数在后面)
        Arrays.sort(strs,(x,y)->(x+y).compareTo(y+x));
        StringBuilder sb = new StringBuilder();
        for(String s:strs)sb.insert(0,s);
        while(sb.length()>1&&sb.charAt(0)=='0')sb.deleteCharAt(0);
        return sb.toString();
    }
}

148. 排序链表（mid）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
class Solution {
    //归并排序
    public ListNode sortList(ListNode head) {
        if(head==null||head.next==null)return head;
        //1.找到中间节点
        ListNode fast = head,slow = head,slowPrev = null;
        while(fast!=null&&fast.next!=null){
            fast = fast.next.next;
            slowPrev = slow;
            slow = slow.next;
        }
        ListNode next = slowPrev.next;
        slowPrev.next = null;
        ListNode headA = sortList(head);
        ListNode headB = sortList(next);
        //3.合并两个有序链表
        return merge(headA,headB);
    }
    //合并两个有序链表
    public ListNode merge(ListNode headA,ListNode headB){
        ListNode dummy = new ListNode(-1);
        ListNode ptr = dummy;
        while(headA!=null&&headB!=null){
            if(headA.val<headB.val){
                ListNode next = headA.next;
                headA.next = null;
                ptr.next = headA;
                headA = next;
            }else{
                ListNode next = headB.next;
                headB.next = null;
                ptr.next = headB;
                headB = next;
            }
            ptr = ptr.next;
        }
        ptr.next = headA==null?headB:headA;
        return dummy.next;
    }
}

56. 合并区间（mid）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
    //排序
    //--
    // --
    public int[][] merge(int[][] intervals) {
        int n = intervals.length;
        if(n<=1)return intervals;
        //排序过后开始时间小的在前面
        Arrays.sort(intervals,(x,y)->x[0]==y[0]?x[1]-y[1]:x[0]-y[0]);
        List<int[]> ret = new ArrayList<>();
        int prevStart = intervals[0][0];
        int prevEnd = intervals[0][1];
        for(int i=1;i<n;i++){
            //有交集
            if(prevEnd>=intervals[i][0]){
                prevEnd = Math.max(prevEnd,intervals[i][1]);if(i==n-1)ret.add(new int[]{prevStart,prevEnd});
            }else{
                ret.add(new int[]{prevStart,prevEnd});
                prevStart = intervals[i][0];
                prevEnd = intervals[i][1];
                if(i==n-1)ret.add(new int[]{prevStart,prevEnd});
            }
        }
        return ret.toArray(new int[ret.size()][]);
    }
}

767. 重构字符串（mid）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
    //奇数位置存放出现数多的，然后用少的插入
    public String reorganizeString(String s) {
        int n = s.length();
        StringBuilder sb = new StringBuilder(s);
        int[] freq = new int[26];
        for(int i=0;i<n;i++)freq[s.charAt(i)-'a']++;
        int maxIndex = 0;
        for(int i=1;i<26;i++){
            if(freq[i]>freq[maxIndex])maxIndex=i;
        }
        if(n-freq[maxIndex]+1<freq[maxIndex])return "";
        PriorityQueue<int[]> queue = new PriorityQueue<>((x,y)->y[1]-x[1]);
        for(int i=0;i<26;i++){
            queue.offer(new int[]{i,freq[i]});
        }
        //奇数位
        int[] cur = queue.poll();
        for(int i=0;i<n;i+=2){
            while (cur[1]==0)cur = queue.poll();
            sb.setCharAt(i,(char) (cur[0]+'a'));
            cur[1]--;
        }
        //剩下的的填充偶数位
        for(int i=1;i<n;i+=2){
            while (cur[1]==0)cur = queue.poll();
            sb.setCharAt(i,(char) (cur[0]+'a'));
            cur[1]--;
        }
        return sb.toString();
    }
}

1353. 最多可以参加的会议数目（mid)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
    //思路：按照开始时间进行排序，取当前能开会的所有会议结束时间压入小堆顶，最后本轮取最早结束的会议参加
    public int maxEvents(int[][] events) {
        int n = events.length;
        //按照开始时间进行排序
        Arrays.sort(events,(x,y)->x[0]-y[0]);
        PriorityQueue<Integer> queue = new PriorityQueue<>();
        int index = 0;
        int day = 1;
        int ret = 0;
        while(index<n||!queue.isEmpty()){
            //将day天能参加的会议全部加入堆，按照结束时间排序
            while(index<n&&events[index][0]==day){
                queue.offer(events[index][1]);
                index++;
            }
            //将已经结束的会议删除
            while(!queue.isEmpty()&&queue.peek()<day)queue.poll();
            //一天只能参加一场会议将结束时间最早的安排
            if(!queue.isEmpty()){
                queue.poll();
                ret++;
            }
            day++;
        }
        return ret;
    }
}

922. 按奇偶排序数组 II（easy）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
class Solution {
    // public int[] sortArrayByParityII(int[] nums) {
    //     int n = nums.length;
    //     //[1,4,2,5,7]
    //     //1,2,4,5,7
    //     int odd = 1;
    //     int even = 0;
    //     for(int i=0;i<n;i++){
    //         if(i%2==0&&nums[i]%2!=0){//偶数位置
    //             //向后查找下标为奇数且值为偶数的下标
    //             while(odd<n&&nums[odd]%2!=0)odd+=2;
    //             swap(i,odd,nums);
    //         }else if(i%2==1&&nums[i]%2!=1){//奇数位置
    //             //向后查找下标为偶数且值为奇数的下标
    //             while(even<n&&nums[even]%2!=1)even+=2;
    //             swap(i,even,nums);
    //         }
    //     }
    //     return nums;
    // }

    // public void swap(int a,int b,int[] nums){
    //     int v = nums[a];
    //     nums[a] = nums[b];
    //     nums[b] = v;
    // }
    //官方的写法
    public int[] sortArrayByParityII(int[] nums) {
        int n = nums.length;
        int j = 1;
        for (int i = 0; i < n; i += 2) {
            if (nums[i] % 2 == 1) {
                while (nums[j] % 2 == 1) {
                    j += 2;
                }
                swap(nums, i, j);
            }
        }   
        return nums;
    }

    public void swap(int[] nums, int i, int j) {
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }
}

976. 三角形的最大周长（easy）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public int largestPerimeter(int[] nums) {
        int ret = 0;
        int n = nums.length;
        Arrays.sort(nums);
        //两边之和大于第三边
        for(int i=n-1;i>=2;i--){
            int a = nums[i];
            int b = nums[i-1];
            int c = nums[i-2];
            if(a<b+c){
                return a+b+c;
            }
        }
        return ret;
    }
}

1356. 根据数字二进制下 1 的数目排序（easy）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
    public int[] sortByBits(int[] arr) {
        int n = arr.length;
        Integer[] clone = new Integer[n];
        for (int i = 0; i < n; i++) {
            clone[i] = arr[i];
        }
        Arrays.sort(clone,(x, y) -> getBit(x)==getBit(y)?x-y:getBit(x)-getBit(y));
        for (int i = 0; i < n; i++) {
            arr[i] = clone[i];
        }
        return arr;
    }
    public int getBit(Integer n){
        int ret = 0;
        for(int i=0;i<32;i++){
            ret+=n&1;
            n>>=1;
            if(n==0)break;
        }
        return ret;
    }
}

973. 最接近原点的 K 个点（mid）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
class Solution {
    //topk问题基于快排，每次划分后只需要排序一边即可
    Random rand = new Random();
    public int[][] kClosest(int[][] points, int k) {
        int n = points.length;
        random_select(points, 0, n - 1, k);
        return Arrays.copyOfRange(points, 0, k);
    }

    public void random_select(int[][] points, int left, int right, int k) {
        int pivotId = left + rand.nextInt(right - left + 1);
        int pivot = points[pivotId][0] * points[pivotId][0] + points[pivotId][1] * points[pivotId][1];
        swap(points, right, pivotId);
        int i = left - 1;
        for (int j = left; j < right; ++j) {
            int dist = points[j][0] * points[j][0] + points[j][1] * points[j][1];
            if (dist <= pivot) {
                ++i;
                swap(points, i, j);
            }
        }
        ++i;
        swap(points, i, right);
        // [left, i-1] 都小于等于 pivot, [i+1, right] 都大于 pivot
        if (k < i - left + 1) {
            random_select(points, left, i - 1, k);
        } else if (k > i - left + 1) {
            random_select(points, i + 1, right, k - (i - left + 1));
        }
    }

    public void swap(int[][] points, int index1, int index2) {
        int[] temp = points[index1];
        points[index1] = points[index2];
        points[index2] = temp;
    }
    //基于堆
    public int[][] kClosest(int[][] points, int k) {
        int n = points.length;
        PriorityQueue<int[]> queue = new PriorityQueue<>(Comparator.comparingDouble(p -> Math.sqrt((p[0] * p[0]) + (p[1] * p[1]))));
        for (int i = 0; i < n; i++) {
            queue.offer(points[i]);
        }
        int[][] ret = new int[k][2];
        int index = 0;
        while(k>index)ret[index++]=queue.poll();
        return ret;
    }
    //基于排序
    public int[][] kClosestSort(int[][] points, int k) {
        Arrays.sort(points,Comparator.comparingDouble(p -> Math.sqrt((p[0] * p[0]) + (p[1] * p[1]))));
        int[][] ret = new int[k][2];
        for (int i = 0; i < k; i++) {
            ret[i] = points[i];
        }
        return ret;
    }
}

1288. 删除被覆盖区间（mid）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    //排序
    //----
    // ----
    // --
    //  -
    public int removeCoveredIntervals(int[][] intervals) {
        int n =intervals.length;
        //按照开始时间排序，开始时间相同按照结束时间长在前
        Arrays.sort(intervals,(x,y)->x[0]==y[0]?y[1]-x[1]:x[0]-y[0]);
        int ret = 0;
        int preStart = intervals[0][0];
        int preEnd = intervals[0][1]; 
        for(int i=1;i<n;i++){
            if(intervals[i][0]>=preStart&&intervals[i][1]<=preEnd){
                ret++;
            }else{
                preStart = intervals[i][0];
                preEnd = intervals[i][1];
            }
        }
        return n-ret;
    }
}

164. 最大间距（hard）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
class Solution {
    //基于桶排序:
    //我们要找出桶的最大最小值且确保桶内的相邻元素差值小于前一个桶最后一位和当前桶第一位之间差值,我们可以通过控制桶的数量来使这个条件成立。
    //
    //证明：
    //1.设长度为 N 的数组中最大最小值为max,min，那么相邻数字的最大间距不会小于 ⌈(max−min)/(N−1)⌉
    //
    //如 [3,6,9,1] max=9,min=1,共4个num,数组中共有3个间隙, 所以相邻数字间距(排序后每个数间隙)不会小于 d = [(max−min)/(N−1)]=[(9-1)/3] = 2
    //
    //2.为什么桶的数量是 (maxVal-minVal)/d+1 = (9-1)/2+1=5
    //
    //因为已知相邻数字间间距大于等于d,如果桶的数量是(maxVal-minVal)/d=(9-1)/2=4,
    //那么每个数占一个桶,那么每个桶的间隙就是大于等于d，如果桶的数量加一,那么必定有一个桶是空的,这样一来,桶间的间距一定大于桶内元素间距
    //
    //通过桶排序每个桶只需记录当前桶的最大最小值
    public int maximumGap(int[] nums) {
        int n = nums.length;
        if (n < 2) return 0;
        //获得最大最小值
        int minVal = Arrays.stream(nums).min().getAsInt();
        int maxVal = Arrays.stream(nums).max().getAsInt();
        //nums相邻元素的最小间隙距离（n-1是间隙个数）
        int d = Math.max(1, (maxVal - minVal) / (n - 1));
        //桶数量
        int bucketSize = (maxVal - minVal) / d + 1;
        //每个桶记录的是当前桶里面的最大最小值
        int[][] bucket = new int[bucketSize][2];
        for (int i = 0; i < bucketSize; ++i) {
            Arrays.fill(bucket[i], -1); // 存储 (桶内最小值，桶内最大值) 对， (-1, -1) 表示该桶是空的
        }
        for (int i = 0; i < n; i++) {
            //确认当前nums[i]所在的桶下标
            int idx = (nums[i] - minVal) / d;
            if (bucket[idx][0] == -1) {
                //初始化设置桶内的最大最小值为nums[i]
                bucket[idx][0] = bucket[idx][1] = nums[i];
            } else {
                //更新桶内的最大最小值
                bucket[idx][0] = Math.min(bucket[idx][0], nums[i]);
                bucket[idx][1] = Math.max(bucket[idx][1], nums[i]);
            }
        }
        //获取最大差值
        int ret = 0;
        int prev = -1;
        for (int i = 0; i < bucketSize; i++) {
            if (bucket[i][0] == -1) {
                continue;
            }
            if (prev != -1) {
                //比较当前桶最小值和前一个桶最大值，即题目所求差值
                ret = Math.max(ret, bucket[i][0] - bucket[prev][1]);
            }
            prev = i;
        }
        return ret;
    }
}

315. 计算右侧小于当前元素的个数（hard)

本题和 剑指 Offer 51. 数组中的逆序对 解题思路类似，采用归并排序，在归并的过程中计算

原始数组 = [8,16,12,100,22] [55,64,7,26,91]

归并排序 L = [8,12,16,22,100] R = [7,26,55,64,91] M = [] (排序后两个指针指向两个数组开始)

                l                                       r

第一轮 L = [8,12,16,22,100] R = [7,26,55,64,91] M = [7] 此时（7<8）所以把7加入M，r向右移一位

                l                                           r

第二轮 L = [8,12,16,22,100] R = [7,26,55,64,91] M = [7,8] 此时（8<26）所以把8加入M，同时新数组中已有1个数且必定小于8，新数组中包含L数组的元素 

                 l                               r                个数是0，所以元素8右侧比8小的元素=M.length-0=1-0=1，l向右移一位

第三轮 L = [8,12,16,22,100] R = [7,26,55,64,91] M = [7,8,12] 此时（12<26）所以把12加入M，同时新数组中已有2个数且必定小于12，新数组中包含L数组的元素

                       l                             r                             个数是1，所以元素12右侧比12小的元素=M.length-1=2-1=1，l向右移一位

第四轮 L = [8,12,16,22,100] R = [7,26,55,64,91] M = [7,8,12,16] 此时（16<26）所以把16加入M，同时新数组中已有3个数且必定小于16，新数组中包含L数组的元素

                            l                         r                             个数是1，所以元素16右侧比16小的元素=M.length-1=3-2=1，l向右移一位

………..

在编码的时候我们需要注意的是记录元素在原数组中的下标位置所以需要建立一个数组来存储。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
class Solution {
    //记录原始数组的下标，在排序的时候跟着更新
    private int[] index;
    //临时存放每轮合并后的新数组，不用每轮都创建数组，遍历完成更新到原始数组
    private int[] temp;
    //临时每轮比较的元素存放值，不用每轮都创建数组，，遍历完成更新到index
    private int[] tempIndex;
    //存放结果值
    private int[] ans;

    public List<Integer> countSmaller(int[] nums) {
        this.index = new int[nums.length];
        this.temp = new int[nums.length];
        this.tempIndex = new int[nums.length];
        this.ans = new int[nums.length];
        //记录下标
        for (int i = 0; i < nums.length; ++i) {
            index[i] = i;
        }
        int l = 0, r = nums.length - 1;
        mergeSort(nums, l, r);
        List<Integer> list = new ArrayList<Integer>();
        for (int num : ans) {
            list.add(num);
        }
        return list;
    }

    public void mergeSort(int[] a, int l, int r) {
        if (l >= r) {
            return;
        }
        int mid = (l + r) >> 1;
        mergeSort(a, l, mid);
        mergeSort(a, mid + 1, r);
        merge(a, l, mid, r);
    }

    public void merge(int[] a, int l, int mid, int r) {
        int i = l, j = mid + 1, p = l;
        while (i <= mid && j <= r) {
            if (a[i] <= a[j]) {//如果排序的两个数组中左边的小于等于右边
                temp[p] = a[i];
                //更新下标
                tempIndex[p] = index[i];
                //记录值
                ans[index[i]] += (j - mid - 1);
                ++i;
                ++p;
            } else {
                temp[p] = a[j];
                tempIndex[p] = index[j];
                ++j;
                ++p;
            }
        }
        while (i <= mid)  {
            temp[p] = a[i];
            tempIndex[p] = index[i];
            ans[index[i]] += (j - mid - 1);
            ++i;
            ++p;
        }
        while (j <= r) {
            temp[p] = a[j];
            tempIndex[p] = index[j];
            ++j;
            ++p;
        }
        for (int k = l; k <= r; ++k) {
            //下标也需要跟着更新
            index[k] = tempIndex[k];
            a[k] = temp[k];
        }
    }
}

相关资料

基础算法 > 刷题记录
#排序算法
算法笔记-排序算法
https://mikeygithub.github.io/2020/02/10/yuque/算法笔记-排序算法/
作者
Mikey
发布于
2020年2月10日
许可协议